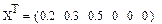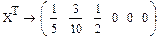Марковские цепи с конечным числом состоянии и непрерывным временем

Определение. Случайный процесс с дискретным временем называется марковским, если на любом шаге S вероятность P (S) перехода системы из состояния i , в состояние jзависитлишь от состояния А в которое попала система на (S—1) шаге, и не зависит от того, как и когда она в это состояние попала. Кратко это свойство формулируют так: при задан­ном настоящем будущее не зависит от прошлого. В силу это­го марковский процесс еще называют процессомбез после­действияили однородным.

Определение. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A_i из полной группы. При этом условная вероятность p_ij(s) того, что в s –ом испытании наступит событие A_j при условии, что в (s – 1) – ом испытании наступило событие A_i, не зависит от результатов предшествующих испытаний.

Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы.

По характеру изменений состояний цепи Маркова можно разделить на две группы.

Определение. Цепью Маркова с дискретным временемназывается цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временемназывается цепь, изменение состояний которой возможно в любые случайные моменты времени.

Определение. Однороднойназывается цепь Маркова, если условная вероятность p_ij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность p_ij называется переходной вероятностью.

Пусть, число состояний конечно и равно k.

Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:

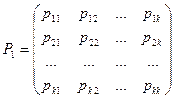
Эта матрица называется матрицей перехода системы.

Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то сумма элементов каждой строки матрицы равна единице.

На основе матрицы перехода системы можно построить граф состояний системы,или размеченный граф состояний.

Пример. По заданной матрице перехода построить граф состояний.

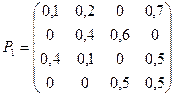
Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.

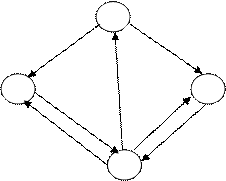
S₁

0,2 0,7

S₂ 0,4 S₄

0,6 0,5

0,1 0,5

S₃

На графе не отмечаются вероятности перехода системы из одного состояния в то же самое.

Пусть P_ij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое p_ij(1) = p_ij.

Тогда вероятность P_ij(n) может быть найдена по формуле, называемой равенством Маркова:

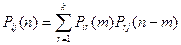
Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r.

Равенство Маркова можно трактовать как видоизмененную формулу полной вероятности.

Используя матрицу перехода Р₁, можно найти вероятности P_ij(2) перехода из состояния i в состояние j за два шага , т.е. матрицу Р₂:

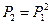
так как при n=2 равенство Маркова – формула умножения матрицы P₁ на P₁ , следовательно, можно получить:

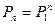
Пример. Задана матрица переходов Р₁. Найти матрицу Р2.

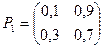
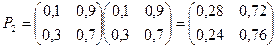
Определение. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими.

Если при некотором п все элементы матрицы Р^п не равны нулю, то такая матрица переходов называется регулярной.

Регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через п шагов из любого состояния. Такие цепи Маркова также называются регулярными.

Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел 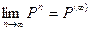и матрица Р^(¥) имеет вид:

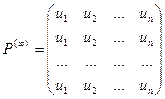
Т.о. матрица Р^(¥) состоит из одинаковых строк. Числа u₁, u₂, …, u_n называются предельными вероятностями.Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы Р^Т (транспонированной к матрице Р).

Собственный вектор полностью определяется из условий:

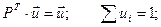
Пример. Найдем предельные вероятности для рассмотренного выше примера.

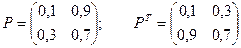
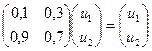
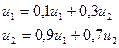
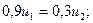
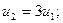
C учетом того, что u₁ + u₂ = 1, получаем:

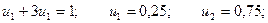
Итак: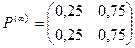

Возможные состояния системы в момент t=m можно охарактеризовать векторами 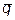^(m)=(q₁^(m), q₂^(m), ..., q_k^(m)),

где q_i^(m) – это вероятность того, что в момент t=m система находится в состоянии А_i.

Используя формулу полной вероятности, нетрудно показать, что имеет место равенство:

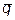^(m+1)= 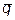^(m)×Р.

Применяя эту формулу последовательно при m=0, 1, 2,... , можно получить выражение для вектора 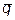^(m) через вектор начальных состояний 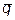⁽⁰⁾ и матрицу вероятностей переходов Р, а именно:

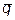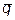^{(m)= (0)×}Р^m.

Предельным распределением вероятностей цепи Маркова называется вектор q^p={q₁, q₂, ..., q_k} такой, что

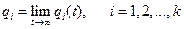
Стационарным распределением называется вектор q={q₁, q₂, ..., q_k}, который удовлетворяет условиям:

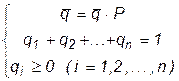
Вектор 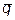определяет распределение вероятностей, которое с течением времени не меняется, т.е. стационарное распределение является также предельным распределением. В развернутом виде система для нахождения координат вектора 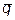, т.е. имеет следующий вид:

(*)

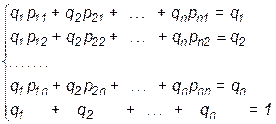Первые n уравнений этой системы являются линейно зависимыми, поэтому любое одно из них можно отбросить. В результате получится система n линейных уравнений, которая почти всегда имеет единственное решение.

По теореме о предельных вероятностях регулярная цепь Маркова имеет предельное распределение вероятностей, которое может быть найдено из системы (*).

Задача 1. Задана матрица P₁ вероятностей перехода дис­кретной цепи Маркова из i-ro в j-oe состояние за один шаг (i, j = 1, 2). Распределение вероятностей по состояниям в началь­ный момент t = 0 определяется вектором .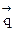

Найти:

1) матрицу P₂ перехода цепи из состояния i в со­стояние j за два шага;

2) распределение вероятностей по состоя­ниям в момент t = 2;

3) вероятность того, что в момент t = 1 со­стоянием будет i = 2;

4) стационарное распределение.

Дано:

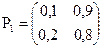
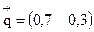
Решение: Для дискретной цепи Маркова в случае её однородности справедливо соотношение ,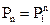

где P₁ – матрица переходных вероятностей за один шаг

P_n – матрица переходных вероятностей за n шагов;

1) Найдем матрицу P₂ перехода за 2 шага.

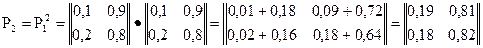
Пусть распределение вероятностей по состояниям на S-ом шаге определяется вектором

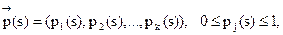
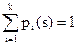
Зная матрицу P_n перехода за n шагов можно определить распределение вероятностей по состоянием на (s+n)-ом шаге.

(4)

,

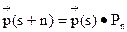2) Найдем распределение вероятностей по состоянием системы в момент t=2. Положим (4) S=0 и n=2. Тогда .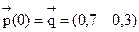

Получим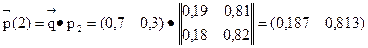

3) Найдем распределение вероятностей по состояниям системы в момент t=1. Положим в (4) S(0) и n=1, тогда

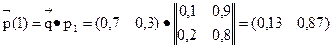
Откуда видно, что вероятность того, что в момент t=1 состоянием цепи будет A₂, равна p₂(1)=0,87.

Распределением вероятностей по состояниям называется стационарным, если оно не меняется от шага к шагу, то есть

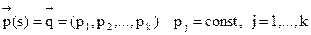
(5)

Тогда из соотношения (4) при n=1 получим 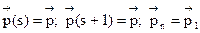или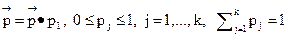

4) Найдем стационарное распределение. Так как k=2 имеем 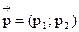. Запишем систему линейных уравнений (5) в координатной форме:

; ; ; ; .

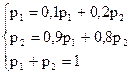
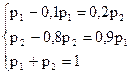
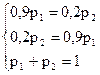
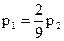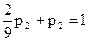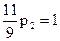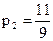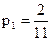Следовательно, .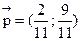

Ответ:

1) матрица перехода за два шага для данной цепи Маркова имеет вид ;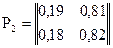

2) распределение вероятностей по состояниям в момент t=2 равно ;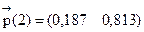

3) вероятность того, что в момент t=1 состоянием цепи будет A₂, равна p₂(1)=0,87;

4) Стационарное распределение имеет вид .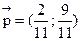

Задача 2. Ремонтная мастерская располагает двумя диагностическими приборами. Известно, что если в какой-то день оба прибора были незаняты, то на следующий день с вероятностью 0,6 они снова окажутся незанятыми и с одинаковыми вероятностями будет занят один или два прибора. Если был занят один прибор, то назавтра с вероятностью 0,2 оба будут свободны и с вероятностью 0,5 – оба заняты. Наконец, если оба прибора были заняты, то назавтра с вероятностью 0,6 оба опять будут заняты и с вероятностью, вдвое меньшей, будет занят только один прибор. Предполагая, что в начале недели (в понедельник) нет никакой информации о занятости приборов, найти вероятность того, что в среду оба прибора будут заняты. Кроме того, найти предельное распределение вероятностей.

Решение. Рассмотрим следующие состояния:

Е₀ – не занят ни один прибор;

Е₁ – занят один прибор;

Е₂ – заняты оба прибора.

Исходя из условия задачи матрица вероятностей переходов имеет вид:

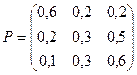
Отсутствие информации в понедельник фактически означает, что вероятности начальных состояний одинаковые, т.е.:

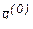=(1/3; 1/3; 1/3).

Вероятности состояний в среду определяются вектором q⁽²⁾.

Имеем:

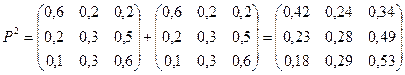
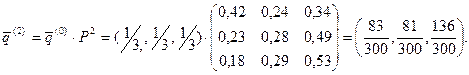
Таким образом, вероятность занятости сразу двух приборов будет равна 136/300.

Предельные вероятности найдем как решение системы:

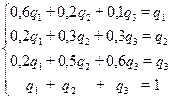
Решая эту систему методом Гаусса, найдем:

q₁=13/51;

q₂=14/51;

q₃=24/51.

Марковские цепи с конечным числом состоянии и непрерывным временем

Пусть физическая система, возможные состояния которой А₁,А₂, .... , А_k может переходить из со­стояния в состояние не в определенные моменты времени, а в любой момент времени случайным образом. При этом воз­никает случайный процесс (цепь) с непрерывным временем.

Если процесс с непрерывным временем обладает отсутствием последействия, то его называют марковским случайным процессом с непрерыв­ным временем или непрерывной цепью Маркова.

Для непрерывной цепи Маркова. вероятность перехода из состояния А_i в состояние А_j в любой момент времени равна нулю. Поэтому вместо вероятности перехода Р_ij рассматривают плотность вероят­ности перехода l_ij которая определяется как предел отно­шения вероятности перехода Р_ij{Dt} за время Dt из состо­яния A_i в состояние A_j; к длине промежутка Dt при Dt 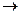0, т. е.

l_ij = 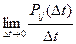. (1)

Плотность вероятности l_ij может быть как постоянной величиной, так и величиной, зависящей от момента времени t, с которого начинается промежуток Dt.

Если плотность ве­роятности перехода l_ij не зависит от t, марковский процесс(цепь) называетсяоднородным.

В дальнейшем будем пред­полагать, что рассматриваемые процессы удовлетворяют ус­ловиюординарности: в один и тот же момент времени t си­стема не может изменить свое состояние более чем один раз.

Из курса дифференциального исчисления известно, что соотношение (1) можно записать в виде Р_ij(Dt)=l_ijDt + a_ij(Dt), где a_ij(Dt)— бесконечно малая высшего порядка по сравнению с Dt. Тогда с точностью до бесконеч­но малой имеем:

P_ij(Dt) = l_ijDt, i 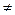j (2)

т. е. вероятность перехода Р_ij(Dt) за малое время Dt равна произведению плотности вероятности перехода l_ij на Dt. По­этому l_ij еще называютинтенсивностью перехода системы из А_i в Aj.

Из величин l_ij составим квадратнуюматрицу интенсивностей переходов:

L = 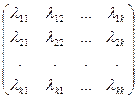(3)

обладающую свойствами:

1) l_ij 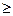0, i 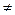j, это следует из (2), так как P_ij(Dt) 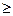0;

2) l_ij 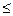0, i=j, так как l_ii = 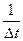(P_ii(Dt) – 1);

3) 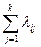= 0 действительно, (l_i1 + l_i2 + … l_ii + … l_ik)Dt = P_i1(Dt) + P_i2(Dt) +…+( P_ii(Dt) – 1) + …+ P_ik(Dt)) = 0.

Интенсивности переходов l_ij удобно задавать на графе состояний. На графе указывают обычно интенсивности l_ij >0.

Зная матрицу интенсивностей переходов или размеченный граф состояний, можно определить вероятности состояний:

p₁ (t), p₂ (t), …, p_k(t), 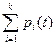= 1, (4)

т. е. вероятности нахождения системы в состоянии А₁, А₂, … , А_k в момент времени t. Вероятности p_i(t) как функции t удовлетворяютсистеме дифференциальных уравнении Колмо­горова, которая в матричной форме имеет вид

p^’(t) = p(t) L (5)

где p^’(t) = ( p₁^’(t), p₂^’(t),…, p_k^’(t)); p(t) = ( p₁(t), p₂(t),…, p_k(t)), L —

матрица интенсивностей переходов (З).

Распределение вероятностей состояний системы называетсястационарным, если оно не меняется с течением времени, т. е. если

p(t) = p, (6)

где p = ( p₁, p₂, …, p_k) = const, j = 1, 2, ..., k. Дифференцируя равенство (6) по t, получим: p^’(t) = 0.

С учетом уравнения (5) приходим к выводу, что стационар­ное распределение удовлетворяет соотно­шению

p L = 0, (7)

т. е. для получения стационарного распределения достаточно в системе дифференциальных уравнений Колмогорова поло­жить p^'_j =0; j =1, 2,.., k.

Уравнения системы (7) не в матричной форме удобно вы­писывать непосредственно по размеченному графику состоя­ний в соответствии со следующим правилом:

сумма произведений l_jip_i, j 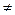i для стрелок, выходящих из i-го состояния, рав­на сумме произведений l_ijp_j, j 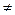iдля стрелок, входящих в i-е состояние.

Задача 2. Задана матрица

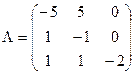
интенсивностей переходов непрерывной цепи Маркова. Со­ставить размеченный граф состояний, соответствующий мат­рице L; выписать систему дифференциальных уравнений Колмогорова для вероятностей состояний; найти стационар­ное распределение вероятностей.

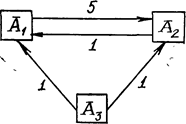
Решение. Размеченный граф должен иметь 3 состояния А₁, А₂, А₃. Из матрицы L находим интенсивности переходов l_ij>0, i 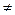j и отмечаем их над соответствующими стрелка­ми (рис. 2). Имеем l₁₂=5, соединяем состояния А₁ и А₂ стрел­кой, направленной от А₁ к А₂, отмечая интенсивность перехода над стрелкой; l₁₃=0, следовательно, состояния А₁ и А₃ стрелкой не соединяем и т. д. Составляем

уравнения Колмогорова: положим в уравнении (5); p(t) = (p₁(t), p₂(t), p₃(t)); p^’(t) = (p₁^’(t), p₂^’(t), p₃^’(t)),

тогда

(p₁^’(t), p₂^’(t), p₃^’(t)) = (p₁(t), p₂(t), p₃(t))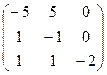

умножая вектор p(t) на матрицу L будем иметь:

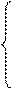p₁^’(t) = - 5 p₁(t) + p₂(t) + p₃(t);

p₂^’(t ) = 5p₁(t) - p₂(t) + p₃(t);

p₃^’(t ) = -2 p₃(t).

Для нахождения стационарного распределения достаточ­но в последней системе дифференциальных уравнений положить все производные p_i^’(t ) = 0, i = 1, 2, 3. Пусть p = (p₁, p₂, p₃)есть стационарное распределение, тогда:

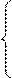0 = - 5 p₁ + p₂ + p₃;

0 = 5p₁ - p₂ + p₃; (8)

0 = -2 p₃.

Решая систему, получим p₃ = 0, p₂= 5p₁. В силу уравнения (4) p₁ + p₂ + p₃ = 1,следовательно, p = ( 1/6; 5/6; 0).

Заметим, что для определения стационарного распределе­ния мы получили бы такую же систему, если бы воспользо­вались правилом, приведенным выше. Действительно, для состояния А₁ имеем 5 p_{1 =} 1 p₂ + 1 p₃ , для состояния А₂: 1 p₂ = 5p₁ + 1 p₃, для состояния A₃: 1 p₃ + 1p₃ = 0. Составляя из этих уравнений систему, убедимся, что она эквивалентна си­стеме(8).

Для многих практических случаев важно знать, как ведут себя вероятности p_i(t}, i=l, 2,..., k при большом времени работы системы, т. е. при t 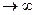. Если при определенных ус­ловиях существуютпредельные вероятности состояний

p_i = 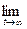p_i(t), i = 1, 2, …, k, (9)

не зависящие от того, в каком состоянии система находилась в начальный момент, то это означает, что с течением времени в системе устанавливаетсяпредельный стационарный режим.

Система, для которой существуют предельные вероятно­сти, называетсяэргодической, а возникающий в ней случай­ный процессэргодическим.

Выясним условия, при которых существуют предельные вероятности состояний. Введем ряд понятий.

Состояние А_i называетсянесущественным, если найдется такое состояние А_j что из A_i в А_j, перейти можно, а из Aj в A_i — нельзя. Состояние A_i называетсясущественным,если оно не является несущественным. Например, для систе­мы, граф состояний которой дан на рис. 2, состояние А₃ не­существенно (так как из него можно перейти в состояние А₁или А₂ но обратно вернуться нельзя), состояния А₁ и A₂ — существенны. Два существенных состояния A_i и A_j назы­ваютсясообщающимися, если из A_i можно попасть в A_j и из A_j в A_i. На рис. 2 представлены сообщающиеся состоя­ния A₁ и А₂.

Теорема 1. Если A_i — несущественное состояние, то

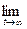p_i(t) = 0. (10)

Смысл этой теоремы состоит в том, что в конечном итоге система выйдет из несущественного состояния A_i и больше в него не вернется.

Теорема 2. Чтобы цепь (процесс) с конечным числом состояний имела единственное стационарное распределение вероятностей, совпадающее с предельным, необходимо и до­статочно, чтобы все ее существенные состояния сообщались между собой.

Пример. В условиях задачи 2 найти предельные веро­ятности состояний.

Решение. В рассматриваемой цепи состояния A₁ и A₂ являются существенными сообщающимися состояниями, A₃ — несущественно. Следовательно, по теореме 2 предель­ное распределение совпадает со стационарным и имеет вид p = ( 1/6; 5/6; 0). Заметим, что результат 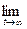p₃(t) = 0 можно было получить непосредственно из теоремы 1, так как состояние A₃ несущественно.

Пример. Задана матрица 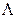интенсивностей переходов непрерывной цепи Маркова. Составить размеченный граф со­стояний, соответствующий матрице 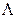; составить систему диф­ференциальных уравнений Колмогорова для вероятностей состояний; найти предельное распределение вероятностей.

Дано:

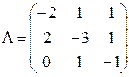
Решение: Однородная цепь Маркова с конечным числом состояний A₁,A₂,…,A_k характеризуется матрицей интенсивностей переходов

,

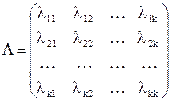где 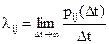- интенсивность перехода цепи Маркова из состояния A_i в состояние A_j;

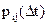- вероятность перехода A_i 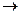A_j за интервал времени .

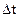Переходы системы из состояния в состояние удобно задавать с помощью размеченного графа состояний, на котором отмечаются дуги, соответствующие интенсивностям .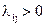

Составим размеченный граф состояний для заданной матрицы интенсивностей переходов.

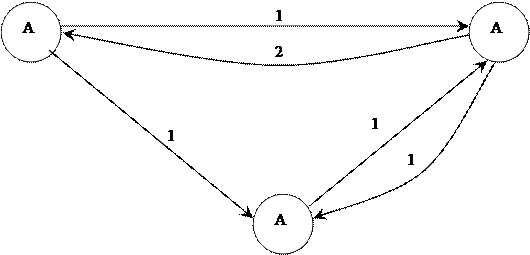
Пусть 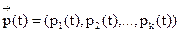- вектор вероятностей 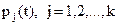, нахождения системы в состоянии A_j в момент t. Очевидно, что 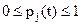и 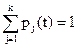. Тогда по правилу дифференцирования векторной функции скалярного аргумента получим 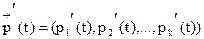. Вероятности 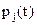удовлетворяют системе дифференциальных уравнений Колмогорова (СДУК), которая в матричной форме имеет вид

(6)

,

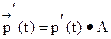Если в начальный момент система находилась в состоянии A_j, то СДУК следует решать при начальных условиях

(7)

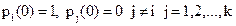
Совокупность СДУК (6) и начальных условий (7) однозначно описывает однородную цепь Маркова непрерывным временем и конечным числом состояний.

Составим СДУК для заданной цепи Маркова. Поскольку k=3, то j=1,2,3. Из соотношения (6) получим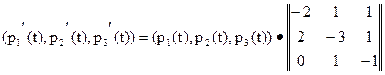

Отсюда будем иметь:

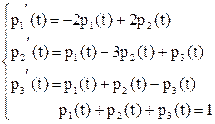
Последнее условие называется нормировочным.

Распределение 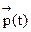вероятностей по состояниям называется стационарным, если оно не меняется с течением времени, то есть 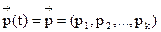, где p_j=const, j=1,2,…,k.

Отсюда 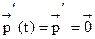. Тогда из СДУК (6) получаем систему для нахождения стационарного распределения 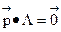, где .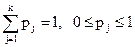

Для данной задачи из СДУК будет иметь

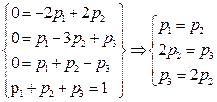
Из нормировочного условия получим

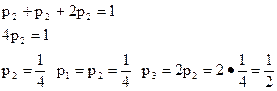
Ответ: предельное распределение имеет вид .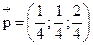

Пример. Определить, существует ли стационарный режим для марковского случайного процесса, размеченный граф состояний которого изображен на рисунке. Если стационарный режим существует, то найти стационарное распределение вероятностей.

Указание.Проведите классификацию состояний системы и примените следствия из теоремы Маркова.

а) Состояние 6 - существенное. Остальные - несущественные состояния. Поэтому единственное стационарное распределение совпадает с предельным.

Для несущественных состояний предельные вероятности равны нулю. Учитывая, что сумма всех вероятностей = 1 получим искомое стационарное распределение:

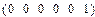
б) Несущественные состояния 1, 2, 6. Состояния 3, 4, 5 - существенные сообщающиеся поэтому единственное стационарное распределение совпадает с предельным.

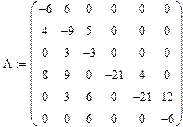
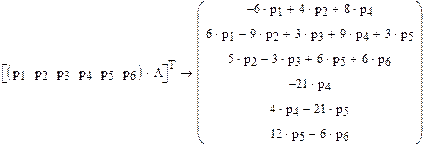
Приравнивая к каждую из строк-уравнений к 0 и учитывая, что сумма вероятностей = 1 получим: