Задача двух тел и сведение её к эквивалентной одномерной

Дана замкнутая система двух материальных точек (тел). Для замкнутой системы функция Лагранжа явно не зависит от времени, значит, потенциальная энергия является функцией только координат. Потенциальная энергия – энергия взаимодействия между телами.

,

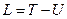
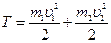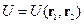
Данная система обладает следующими свойствами:

1. Пространство однородно и изотропно. Это значит, что систему можно транслировать.

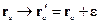
Вследствие однородности пространства:

.

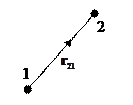
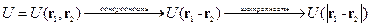Мы можем вращать вектор 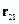как хотим, решение от этого не измениться (следствие изотропности). Введём новые координаты:

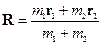
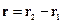
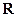- описывает положение центра масс (система как целое).

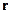- описывает относительное положение точек.

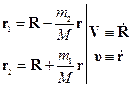
где .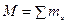

Таким образом .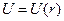

,

,

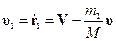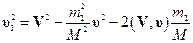
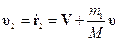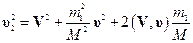
Имеем:

,

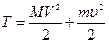
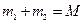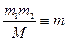
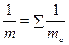- приведённая масса.

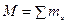- общая масса.

В итоге:

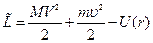
Была функция Лагранжа 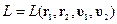, а стала 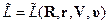. И в первом и во втором случае имеем 6 степеней свободы, т.е. мы ничего не потеряли.

Здесь 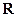- циклическая координата. Тогда

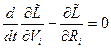
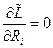, тогда:

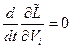- интеграл движения

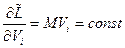- закон сохранения импульса

;

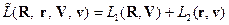
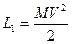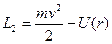
Итак, задача двух тел свелась к решению двух задач:

1.Свободная материальная точка массой .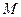

2.Материальная точка массы 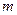во внешнем центральном стационарном поле(относительное движение). 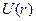зависит от модуля 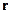, значит поле центральное или сферически-симметричное.

Особенности движения частицы в центральном поле.

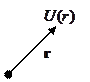
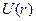- закон взаимодействия.

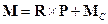
здесь , ,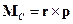

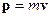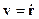
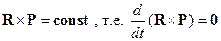
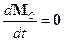- но это равенство имеет место, лишь, если начало координат выбрано в центре поля.

По функции 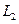можно показать, что 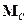- интеграл движения. Далее будем писать 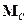без индекса - .

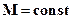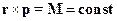
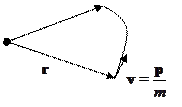Так как 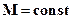, то сохраняется модуль и направление вектора. Значит, движение осуществляется в плоскости, то есть имеет две степени свободы. Перейдем к полярным координатам:

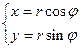
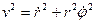
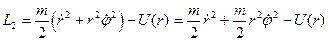
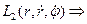
- циклическая координата

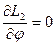
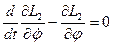
тогда 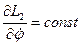- закон сохранения для координаты .

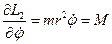-закон сохранения момента импульса.

Роль 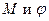: - обобщённая координата, 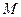- обобщённый для неё импульс, т.е.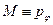

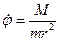
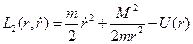
Мы свели задачу двух тел к одномерной задаче, т.к. здесь одна обобщённая координата. Далее:

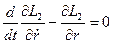
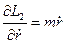-обобщённый импульс, соответствующий координате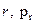

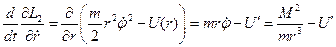
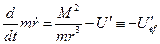
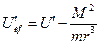
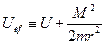
здесь .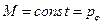

Одномерный эффективный потенциал.

Рассмотрим график одномерного эффективного потенциала:

, ,

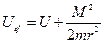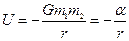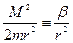
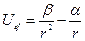
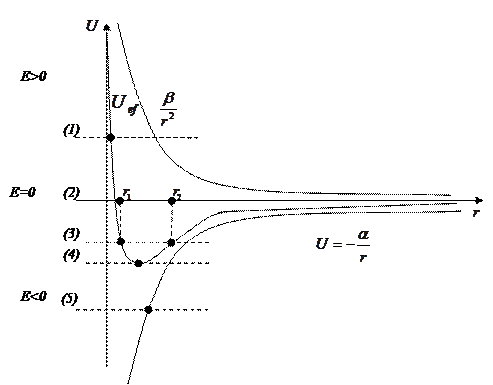
Финитное движение – движение, происходящее в ограниченной части пространства.

(1) – инфинитное движение (гипербола).

(2) – движение (инфининтное) идет по параболе E=0.

(3) – движение (финитное) идёт по эллиптической траектори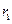и, и 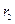- точки поворота.

(4) – движение по окружности.

(5) – падение на центр тяготения.