Внимание: без кассеты ПИ/09 можно получить прямоугольный сигнал непосредственно с генератора

2 Установите следующие значения параметров выходного напряжения генератора: частота 1 кГц, напряжение 2 В.

3 Получите на экране осциллографа последовательность прямоугольных импульсов и убедитесь в соответствии отображаемых параметров установленным на генераторе.

4 Установите на магазинах сопротивлений и емкостей следующие значения: R₁ = 100 Ом, R₂ = 1 кОм, С = 1·10^-2 мкФ.

5 Получите на экране осциллографа изображение импульсов зарядки и разрядки конденсатора. С помощью ручек «Вольт/делен», «синхронизация», и «время/делен» добейтесь устойчивого неподвижного изображения токов зарядки и разрядки конденсатора.

6 Зарисуйте координатную сетку экрана осциллографа в масштабе и кривые импульсов. Определите время релаксации t (рисунок 8.2, б), емкость конденсатора по известному сопротивлению и максимальное напряжение в импульсе. Вычислите время релаксации цепи t расчетным путем и сравните ее со значением, найденным экспериментально. Найдите среднюю арифметическую ошибку измерений.

7 Повторите пункты 5–6 для других параметров R и С, причем подберите их так, чтобы осциллограммы зарядки-разрядки конденсатора выглядела как на рисунке 8.5 (пунктирные линии).

U

U0

t

t1

t2

t3

t4

Рисунок 8.5 – Осциллограмма процесса зарядки-разрядки

конденсатора

8 Не изменяя параметров схемы, подключите вход «Y» осциллографа к выходу сопротивления R₁ и зарисуйте осциллограмму напряжения U_R(рисунок 8.2).

Тема 9

Изучение работы простых цепей

1 Фазовые соотношения в простых цепях

2 Коэффициент передачи

3 Амплитудочастотная и фазочастотная характеристики простых цепей

Основные понятия по теме

Цепь, содержащая два резистора

Схема (рисунок 9.1) представляет собой резистивный делитель, имеющий две пары внешних зажимов. Обозначим входные зажимы U₁, выходные – U₂. Коэффициент передачи цепи по напряжению 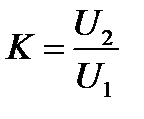. Коэффициент передачи К является важнейшей характеристикой цепи, поскольку дает возможность рассчитать напряжение на выходе по известному напряжению на входе.

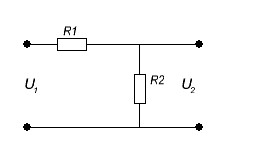
Рисунок 9.1 – Схема резистивного делителя

Зададим для цепи (рисунок 9.1) напряжение на входе U₁. Тогда действующее значение тока 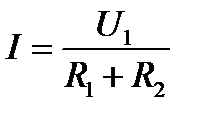. Действующее значение напряжения на выходе можно записать в виде

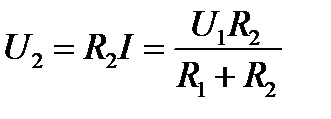(9.1)

Коэффициент передачи равен

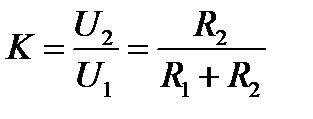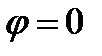, (9.2)

Если на вход резистивного делителя подавать сигнал различных частот с генератора, то, пренебрегая паразитными емкостями, можно установить, что коэффициент передачи не будет изменяться.

Запомните, что в цепи с активным сопротивлением ток и напряжение совпадают по фазе. Электрическая мощность в активном сопротивлении преобразуется в тепло.

Цепь, содержащая R и C

На рисунке 9.2 показан делитель напряжения, состоящий из конденсатора и резистора.

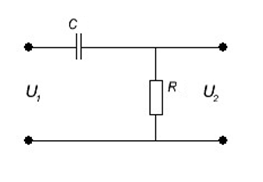
Рисунок 9.2 – Делитель напряжения,

состоящий из конденсатора и резистора

Согласно закону Ома для комплексных величин, комплексный входной ток

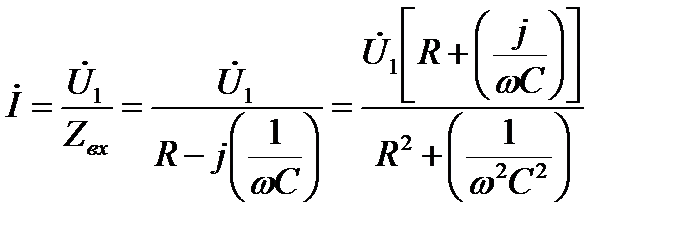
Напряжение на резисторе R равно

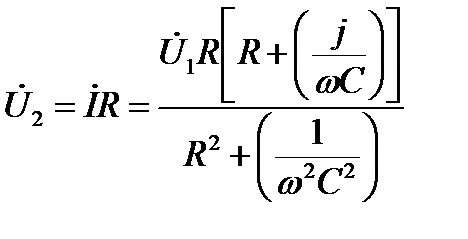(9.3)

Здесь точкой сверху обозначены комплексные величины. Сравните полученный результат с выражением для резистивного делителя (9.1).

Для постоянного тока идеальный конденсатор характеризуется бесконечно большим сопротивлением, не позволяющим проходить постоянному току. Для переменного тока с частотой f реактивное сопротивление конденсатора с емкостью C, или емкостное сопротивление, выражается формулой:

.

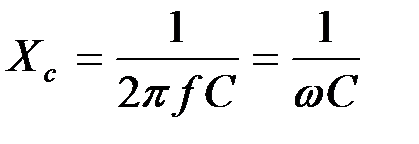Реактивное сопротивление вызывает сдвиг фаз между током и напряжением (ток в цепи с емкостью без активного сопротивления опережает напряжение на 90°). В цепи, содержащей R и C, сдвиг фаз φ между током и напряжением будет меньше 90°: .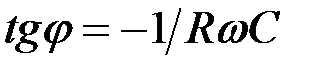

Возвращаясь к рисунку 9.2, заметим, что входное сопротивление 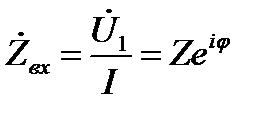. При изменении частоты сопротивление реактивных элементов цепи изменяется. Зависимость модуля комплексного входного сопротивления цепи от частоты называют входной амплитудно-частотной характеристикой цепи (АЧХ): Z_вх = Z_вх(w). Аналогично, входной фазочастотной характеристикой цепи (ФЧХ) называют зависимость аргумента комплексного входного сопротивления от частоты j_Zвх = j(w).

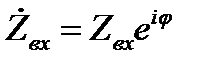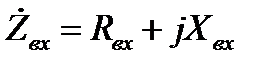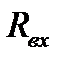Комплексное входное сопротивление можно представить не только в показательной , но и в алгебраической форме , где и 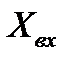– резистивная и реактивная составляющая комплексного входного сопротивления. Частоту w_гр, на которой реактивная составляющая входного сопротивления цепи по абсолютному значению равна резистивной составляющей, называют граничной.

График АЧХ для схемы (рисунок 9.2) представлен на рисунке 9.3. Как вы видите, график представляет фильтр высоких частот. На высоких частотах выходное напряжение приблизительно равно входному 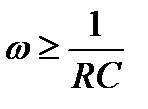, а на низких частотах выходное напряжение уменьшается до нуля.

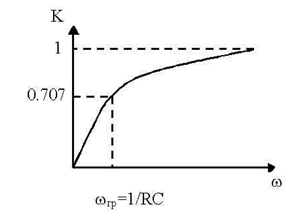
Рисунок 9.3 – Фильтр высоких частот

Если поменять местами R и C, то фильтр будет вести себя противоположным образом в отношении частоты, получим фильтр низких частот (рисунок 9.4).

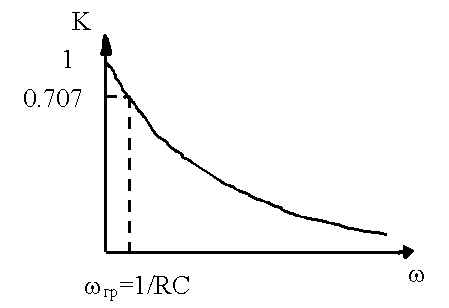
Рисунок 9.4 – Фильтр низких частот

Для схемы (9.2)

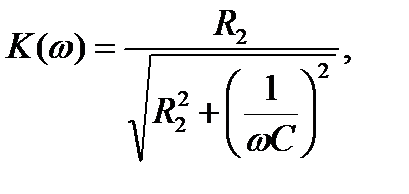(9.4)

а ФЧХ имеет вид

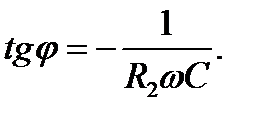(9.5)

Цепь, содержащая R и L

Очевидно, что для RL-цепи справедливы формулы:

;

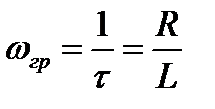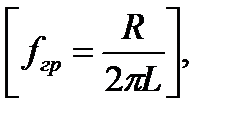
а для RC-цепи выполняются соотношения:

; .

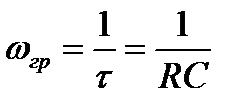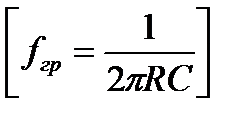Для RL-цепи можно записать

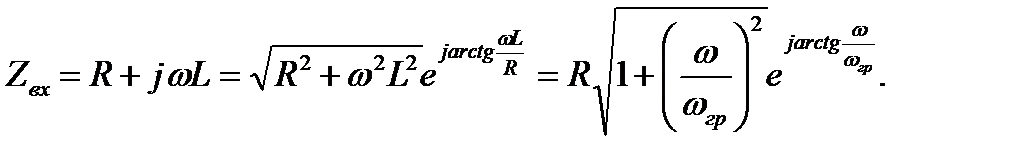
Итак, входную АЧХ последовательной RL-цепи вычисляют согласно выражению 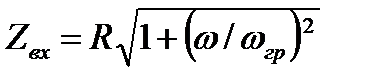, а входную фазочастотную характеристику

.

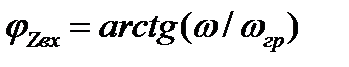При w = 0 имеем 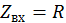, j = 0.

При w = w_гр получаем 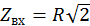, j = 45⁰.

При w = ¥ находим 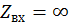, j = 90⁰.

Кривые Z_вх = f(w) и j_zвх = f(w) для RL-цепи показаны на рисунке 9.5 а, б.

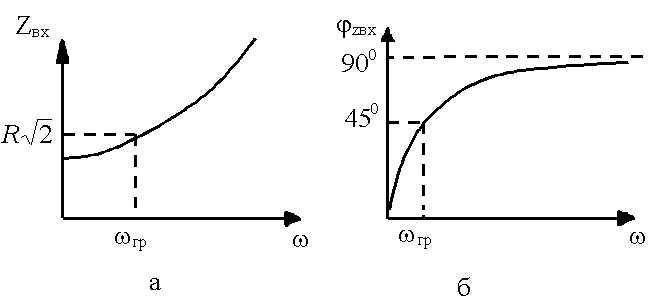
Рисунок 9.5 – Кривые Z_вх = f(w) и j_zвх = f(w) для RL-цепи

Комплексная передаточная функция цепи по напряжению равна

.

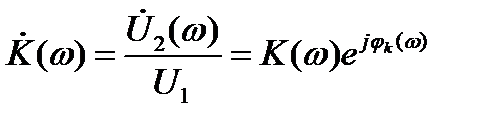Коэффициент передачи цепи К и угол сдвига фазы j выражается формулами:

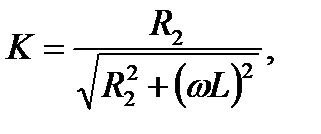(9.6)

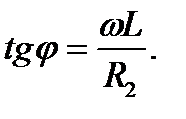(9.7)

Вопросы для самоконтроля

1 Дайте определение простых линейных цепей.

2 Приведите фазовые соотношения между входным и выходным напряжением в простых цепях с реактивными элементами.

3 Найдите расчетным путем коэффициенты передачи в простых цепях.

4 Поясните АЧХ и ФЧХ простых цепей.

Лабораторная работа 9