Перевірка гіпотези про незалежність двох випадкових величин
Нехай проведено n експериментів, результати яких є значеннями дискретних випадкових величин 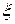 і
і 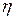 , які приймають відповідно значення x1, x2, …, xm і y1, y2, …,yl.
, які приймають відповідно значення x1, x2, …, xm і y1, y2, …,yl.
Позначимо через kij число експериментів, в яких 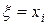 і
і 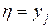 ,
, 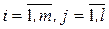 . Якщо
. Якщо 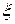 і
і 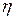 - неперервні випадкові величини, то область значень кожної з них розбивається на скінченне число інтервалів. В цьому випадку
- неперервні випадкові величини, то область значень кожної з них розбивається на скінченне число інтервалів. В цьому випадку 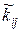 - число експериментів, в яких випадкова величина
- число експериментів, в яких випадкова величина 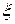 попала в i – ий інтервал, а випадкова величина
попала в i – ий інтервал, а випадкова величина 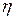 в j – ий інтервал. Результати n експериментів можна представити у таблиці спряженості ознак розміру m*l (Таблиця 4.3)
в j – ий інтервал. Результати n експериментів можна представити у таблиці спряженості ознак розміру m*l (Таблиця 4.3)
Таблиця 4.3.
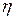 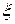 | y1 | y2 | … | yl | 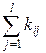 |
| x1 | k11 | k12 | … | k1l | k1. |
| x2 | k21 | k22 | … | k2l | k2. |
| … | … | … | … | … | … |
| xm | km1 | km2 | kml | km. | |
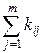 | k.1 | k.2 | … | k.l | k..=n |
Перевіряється нульова гіпотеза H0, яка стверджує, що випадкові величини 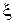 і
і 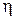 незалежні. Якщо гіпотеза H0 вірна, то за означенням
незалежні. Якщо гіпотеза H0 вірна, то за означенням
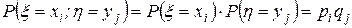 .
.
Нехай 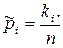 і
і 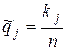 - оцінки ймовірностей
- оцінки ймовірностей 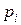 і
і 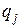 . Якщо гіпотеза H0 вірна, то теоретичні частоти
. Якщо гіпотеза H0 вірна, то теоретичні частоти 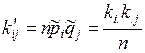 .
.
Для перевірки гіпотези H0 за допомогою критерію 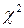 використовують статистику
використовують статистику
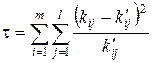 , (4.13)
, (4.13)
яка при справедливості гіпотези H0 і для 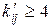 має розподіл
має розподіл 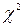 з (m-1)(l-1) ступенями свободи.
з (m-1)(l-1) ступенями свободи.
Нехай 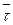 точкова оцінка випадкової величини
точкова оцінка випадкової величини 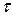 . Тоді для заданого рівня значущості
. Тоді для заданого рівня значущості 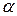 критична область
критична область 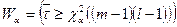 , де
, де 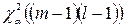 знаходять за таблицею 5 у додатку.
знаходять за таблицею 5 у додатку.
Для зручності обчислень, формулу (4.13) можна переписати у виді
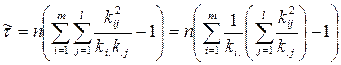 . (4.14)
. (4.14)
Якщо теоретичні частоти 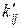 для деяких кліток таблиці 4.3 не задовольняють умову
для деяких кліток таблиці 4.3 не задовольняють умову 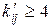 , то відповідні рядки і стовпці повинні бути об’єднані з сусідніми рядками і стовпцями.
, то відповідні рядки і стовпці повинні бути об’єднані з сусідніми рядками і стовпцями.
Якщо 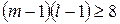 і
і 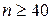 , то мінімально допустиме значення теоретичних частот може бути рівним одиниці.
, то мінімально допустиме значення теоретичних частот може бути рівним одиниці.
Випадкові величини 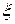 і
і 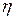 можна розглядати як дві ознаки, за якими класифікується вибірка об’єму n; незалежність
можна розглядати як дві ознаки, за якими класифікується вибірка об’єму n; незалежність 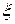 і
і 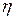 відповідає незалежності цих ознак.
відповідає незалежності цих ознак.
В багатьох випадках потрібно перевірити гіпотезу про однорідність декількох вибірок, або, іншими словами, гіпотезу про те, що ці вибірки одержані з одної генеральної сукупності. Якщо перевіряється однорідність m різних вибірок з об’ємами n1, n2, …,nm і вони можуть бути записані у виді таблиці 4.3, то можна використовувати той же критерій, що і для перевірки незалежності двох ознак.
Приклад 4.6. Проводився аналіз результатів (в балах) вступних випробувань з математики і української мови на трьох спеціальностях (результати розбили на дві групи: (>60; 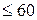 ) і отримали наступний розподіл:
) і отримали наступний розподіл:
| Бали | Всього | |||
| >60 | ||||
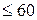 | ||||
| Всього |
Чи можна вважати, що для рівня значущості 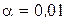 результати вступних випробувань залежать від вибраної спеціальності.
результати вступних випробувань залежать від вибраної спеціальності.
Розв’язок. За формулою (4.14) знаходимо:
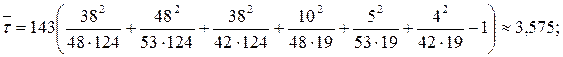
число ступенів свободи k=(2-1)(3-1)=2. За таблицею 5 додатку 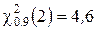 . Оскільки 3,575<4,6, то результати вступних випробувань не залежать від вибраної спеціальності.
. Оскільки 3,575<4,6, то результати вступних випробувань не залежать від вибраної спеціальності.
Зауважимо, що твердження про те, що результати випробувань не залежать від вибраної спеціальності можна трактувати як перевірку гіпотези про однорідність трьох вибірок об’ємами 48, 53, 42.
