Понятия величин, входящих в уравнение I-го закона термодинамики.
Внутренняя энергия газа.
Внутренняя энергия вещества представляет собой сумму кинетической и потенциальной энергий микрочастиц.
В процессах изучаемых технической термодинамикой учитываются следующие составляющие внутренней энергии: кинетическая энергий поступательного и вращательного движения молекул, кинетическая энергия внутримолекулярных колебаний атомов и потенциальная энергия взаимодействия между молекулами.
Согласно представлениям М.К.Т. внутренняя кинетическая энергия полностью определяется температурой. Внутренняя потенциальная энергия зависит при данной температуре от удельного объема, которым определяется расстояние между молекулами.
Внутренняя энергия в целом является функцией состояния рабочего тела.
(Внутренняя энергия реального газа однозначно определяется двумя параметрами состояний;)
Внутренняя энергия идеального газа является функцией только температуры. Изменение внутренней энергии в процессе полностью определяется начальным и конечным состояниями рабочего тела и не зависит от характера процесса. Это значит, что величина 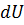 является полным дифференциалом и
является полным дифференциалом и 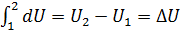
Если изменение состояния рабочего тела происходит при постоянном 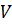 , то внешняя работа не совершается (
, то внешняя работа не совершается ( 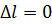 ) и согласно I-му закону термодинамики, теплота расходуется только на увеличение внутренней энергии.
) и согласно I-му закону термодинамики, теплота расходуется только на увеличение внутренней энергии.
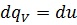
В этом случае подводимая теплота 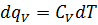 , где
, где 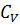 - теплоемкость 1 кг газа при постоянном
- теплоемкость 1 кг газа при постоянном 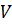 .
.
Отсюда:
|
Абсолютные значения внутренней энергии обычно не нужны в расчетах. Важно знать ее изменение 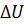 при переходе рабочего тела из одного состояния в другое.
при переходе рабочего тела из одного состояния в другое.
Для наиболее распространенных газов значение внутренней энергии приводится в таблицах.
|
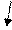 Внешняя работа.
Внешняя работа. 
Рассмотрим однородное тело имеющее массу 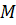 , объем
, объем 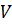 , поверхность
, поверхность 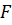 , и находящееся под внешним давлением
, и находящееся под внешним давлением 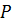 , уравновешенным упругостью тела.
, уравновешенным упругостью тела.
При сообщении из вне теплоты 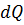 , объем тела увеличится на
, объем тела увеличится на 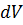 и будет произведена работа расширения
и будет произведена работа расширения 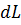 .
.
Бесконечно малое увеличение объема происходит в результате перемещения каждой точки поверхности тела по нормали на расстояние 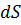 .
.
Поэтому 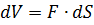
На всю поверхность тела действует сила 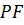 , против которой совершается работа расширения.
, против которой совершается работа расширения.
Таким образом:
|
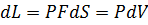
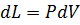 и
и
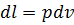 и
и
Уравнение I закона 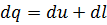
Для внешней работы: 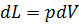 L=
L= 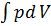
l= 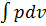
Интеграл можно брать тогда, когда известны зависимость p от 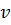 (p от v)
(p от v)
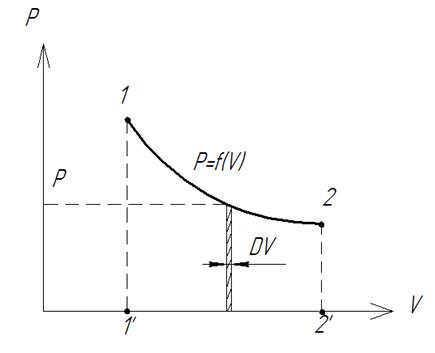
Заштрихованный элемент 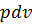 представляет собой элем. Работу
представляет собой элем. Работу 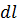 . Для всего процесса
. Для всего процесса 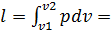 площадь 1-2-2’-1’. Следовательно, на диаграмме
площадь 1-2-2’-1’. Следовательно, на диаграмме  площадь под кривой процесса представляет в определенном масштабе удельную работу расширения.
площадь под кривой процесса представляет в определенном масштабе удельную работу расширения.
Если газ расширяется, ( 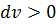 ), то он совершает положительную работу.
), то он совершает положительную работу.
Если газ сжимается под действием внешних сил ( 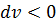 ), то работа отрицательна.
), то работа отрицательна.
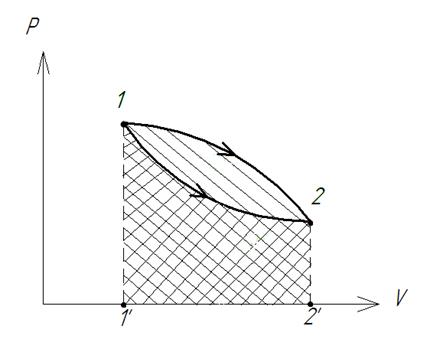
Этот рисунок показывает, что величина работы определяется зависимостью 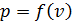 (характером процесса) и не может быть определена лишь по положению начальной и конечной точек процесса. Из этого следует, что в отличие от внутренней энергии внешняя работа
(характером процесса) и не может быть определена лишь по положению начальной и конечной точек процесса. Из этого следует, что в отличие от внутренней энергии внешняя работа 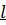 является функцией процесса, а не функцией состояния. Элементарная работа
является функцией процесса, а не функцией состояния. Элементарная работа 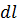 не является полным дифференциалом. Для всего процесса
не является полным дифференциалом. Для всего процесса
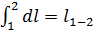 или просто
или просто 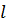
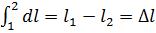 - такая запись была бы неверна т.к. говорить о приращении работы в процессе так же бессмысленно как о величине работы в каком-либо состоянии газа.
- такая запись была бы неверна т.к. говорить о приращении работы в процессе так же бессмысленно как о величине работы в каком-либо состоянии газа.
Теплота процесса
В уравнении I-го закона 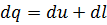 элемент. Теплота
элемент. Теплота 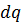 представляет собой алгеброическую сумму двух величин, одна из которой
представляет собой алгеброическую сумму двух величин, одна из которой 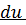 -не зависит от характера процесса, а вторая
-не зависит от характера процесса, а вторая 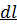 – зависит, следовательно,
– зависит, следовательно, 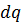 так же зависит от характера процесса и не является полным дифференциалом. Подобно работе, теплота
так же зависит от характера процесса и не является полным дифференциалом. Подобно работе, теплота 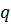 является функцией процесса и для конечного процесса:
является функцией процесса и для конечного процесса:
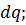
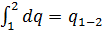 или просто
или просто 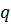 .
.
Покажем это на примере перехода рабочего тела из состояния 1 в состояние 2 тремя путями.
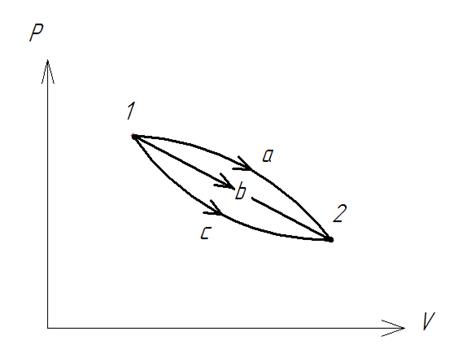
Изменение внутренней энергии 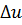 определяется только начальными и конечными состояниями:
определяется только начальными и конечными состояниями:
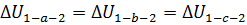
Из рисунка видно, что 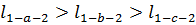
Тогда на основании I закона термодинамики: 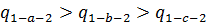 ;
;
При подводе теплоты к рабочему телу, 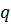 имеет знак (+), при отводе теплоты – знак (-).
имеет знак (+), при отводе теплоты – знак (-).
Уравнение I закона для конечного процесса
В диф. форме уравнение 1-го закона имеет вид: 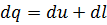 , мы вычислили, что
, мы вычислили, что 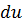 является полным дифференц., а
является полным дифференц., а 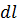 и
и 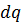 не является, поэтому для конечного процесса:
не является, поэтому для конечного процесса:
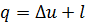 – для 1 кг
– для 1 кг
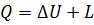 - для М (кг)
- для М (кг)
В зависимости от термодинамического процесса любой член уравнения может быть >0; <0; =0.
Энтальпия
Эта функция вводится математическим путем Э.
Определяется выражением:
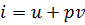 - для 1 кг.
- для 1 кг.
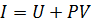 - для М кг.
- для М кг.
Размерность энтальпии совпадает с размерностью внутренней энергии
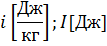
Входящие в выражения для 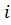 величины
величины 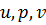 представляют собой функции и параметры состояния, поэтому Э.так же является функцией состояния.
представляют собой функции и параметры состояния, поэтому Э.так же является функцией состояния.
Э. равна сумме внутренней энергии и потенциальной энергии давления 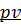 .
.
Потенциальную энергию давления можно рассматривать, как работу вытеснения телом, имеющего объем 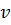 , внешней среды с давлением p. Особенность энтальпии заключается в том, что в нее входит параметр внешней среды –
, внешней среды с давлением p. Особенность энтальпии заключается в том, что в нее входит параметр внешней среды – 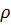 .
.
Поэтому Э. характеризует энергию расширенной системы – рабочего тела и внешней среды.
Во всех случаях, когда рассматриваем равновесные состояния и процессы, давление p является так же параметром состояния рабочего тела.
Так как 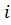 есть функция состояния, то
есть функция состояния, то 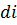 является полным дифференциалом этой функции:
является полным дифференциалом этой функции:
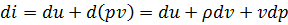
Для конечного процесса:
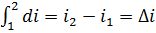
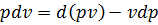
Уравнение I закона термодинамики в диф.форме можно записать так:
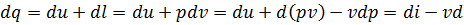
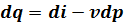 - I закон записан с помощью энтальпии
- I закон записан с помощью энтальпии
При 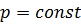 получим:
получим: 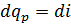 следовательно, дифференциал энтальпии равен элементарному количеству теплоты подводимому или отводимому в процессе при
следовательно, дифференциал энтальпии равен элементарному количеству теплоты подводимому или отводимому в процессе при 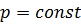 .
.
Для конечного процесса:
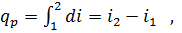 т.е. вся теплота в изобарном процессе расходуется на изменение энтальпии.
т.е. вся теплота в изобарном процессе расходуется на изменение энтальпии.
Энтальпия идеального газа, для которой справедливо уравнение состояния:
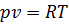 равна
равна 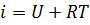 ;
;
А дифференциал энтальпии:
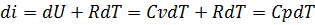
Следовательно, энтальпия идеального газа является функцией одной температуры.
Изменение энтальпии во всех процессах идеального газа определяется по формуле:
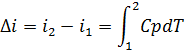
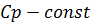 при p=const
при p=const
Энтальпия реального газа определяется двумя параметрами состояния.
Практический интерес представляет 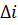 , а не ее абсолютное значение, поскольку между i и u существует однозначная связь, начало отсчета энтальпии связано с началом отсчета внутренней энергии. Для наиболее распространенных газов значение энтальпии приводится в таблицах термодинамических характеристик газа.
, а не ее абсолютное значение, поскольку между i и u существует однозначная связь, начало отсчета энтальпии связано с началом отсчета внутренней энергии. Для наиболее распространенных газов значение энтальпии приводится в таблицах термодинамических характеристик газа.
Эффективный коэффициент полезного действия тепловых двигателей и установок.
В реальных двигателях невозможно избежать ряда потерь энергии. Для оценки полноты использования теплоты, выделяющейся при сгорании топлива пользуются понятием эффективный коэф. полезного действия.
Эффективный КПД – отношение полученной от двигателя полезной работы L, ко всей теплоте Qзатраченное
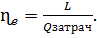
Э. КПД учитывает все потери энергии в реальном тепловом двигателе или установке и этим отличаются от других КПД учитывающих отдельные потери.
Пользуясь ед. СИ.
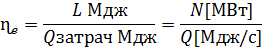
Где 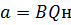
В последнем выражении N Мвт – мощность установки; Q МДж/с –секундный расход теплоты;
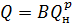
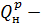 теплота сгоревшего топлива (низшая).
теплота сгоревшего топлива (низшая).
B – секундный расход топлива.
В процессах сгорания топлива содержится водяной пар. Низкая теплота сгорания получается без учета теплоты выделяющейся при конденсации водяного пара. Высшая т.е. – без учета этой теплоты.
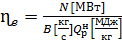 числитель и знаменатель делим на мощность N:
числитель и знаменатель делим на мощность N:
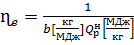 где
где 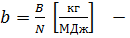 удельный расход топлива
удельный расход топлива
Таким образом:
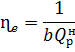
в технической литературе можно встретить другие выражения для 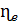 в которой применяется прежние единицы измерения энергии
в которой применяется прежние единицы измерения энергии
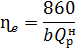
b – кг/кВт*ч
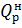 – ккал/кг.
– ккал/кг.

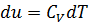 ;
; 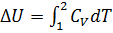
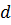 -перемещение каждой точки поверхности по нормали
-перемещение каждой точки поверхности по нормали 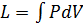 (для
(для 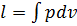 (для 1 кг)
(для 1 кг)