Интерпретация параметров моделей

Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:

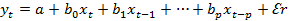(1)

Данная модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной x, то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.

Коэффициент регрессии Ь_О при переменной x_t характеризует среднее абсолютное изменение yt при изменении X_t на 1 ед, своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора x. Этот коэффициент называют краткосрочным мультипликатором.

В момент t+1 совокупное воздействие факторной перемен­ ной X_t на результат Yt составит (Ь_О + Ь.) усл. ед., в момент t+2 это воздействие можно охарактеризовать суммой (Ь_О + Ь. + Ь₂) и т.д. Полученные таким образом суммы называют промежуточными мультипликаторами.

С учетом конечной величины лага можно сказать, что изме­ нение переменной х, В момент t на 1 усл. ед. приведет к общему изменению результата через l моментов времени на (Ь_О + Ь. + ... + b₁)абсолютных единиц.

Введем следующее обозначение:

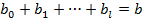(2)

Величину Ь называют долгосрочным мультипликатором, который показывает абсолютное изменение в долгосрочном периоде t+1 результата y под влиянием изменения на 1 ед. фактора.

Предположим, 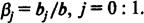(3)(3)

Назовем полученные величины относительными коэффициентами модели с распределенным лагом. Если все коэффициенты bj имеют одинаковые знаки, то для любого j:

0<βj<1 и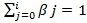

В этом случае относительные коэффициенты βj являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения результативного признака в момент времени (t + j). " .

Зная величины β_j, с помощью стандартных формул можно определить еще две важные характеристики модели множественной регрессии: величину среднего лага и медианного лага. Средний лаг определяется по формуле средней арифметической взвешенной:

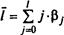(4) и представляет собой средний период, в течение которого будет происходить

изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.

Медианный лаг – величина лага, для которой

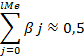
Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.

Обратимся к модели авторегрессии. Пусть имеется следущая модель:

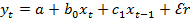
Как и в модели с распределенным лагом, bo, в этой модели характеризует краткосрочное изменение yt под воздействием изменения xt на 1ед. Однако, промежуточный и долгосрочный мультипликаторы иные. К моменту времени t на bo единиц, а yt+1 под воздействием своего изменения в непосредственно предшествующий момент времени на С1 единиц. Т.о. общее абсолютное изменение результата составит boC1 единиц и т.д.

Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточного мультипликаторов:

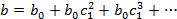(6)

Учитывая, что практически во все модели авторегрессии вводится так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной Yt-1 по абсолютной величине меньше 1 , |C1|<1, соотношение (6)можно преобразовать следующим образом:

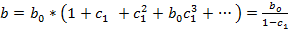(7)

Такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.