Варіанти індивідуальних завдань до теми v
Варіант 1.
1.Знайти форму рівноваги прямокутної мембрани зі сторонами 2а та 2с (початок координат вибраний у центрі мембрани), яка знаходиться під дією рівномірно розподіленого навантаження  якщо краї мембрани нерухомо закріплені. Обчислити прогин центру мембрани, вважаючи відношення с:а=2.
якщо краї мембрани нерухомо закріплені. Обчислити прогин центру мембрани, вважаючи відношення с:а=2.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
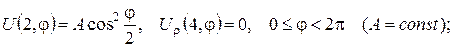
б) 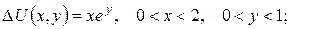
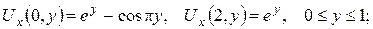
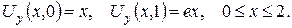
3.Знайти об’ємний потенціал мас, розподілених зі сталою густиною 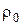 у сферичному шарі a≤r≤b, де 0<а<b.
у сферичному шарі a≤r≤b, де 0<а<b.
Варіант 2.
1.Знайти закон стаціонарного розподілу температури всередині нескінченого кругового циліндра радіуса 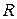 , якщо на його поверхні підтримується температура
, якщо на його поверхні підтримується температура 
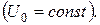 Розв’язок знайти у формі ряду та у формі інтеґралу Пуассона.
Розв’язок знайти у формі ряду та у формі інтеґралу Пуассона.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 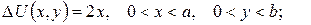
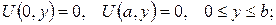
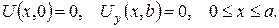
б) 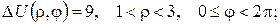
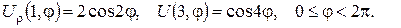
3.Знайти лоґарифмічний потенціал подвійного шару відрізка 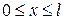 з густиною моментів
з густиною моментів 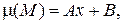 де А, В – задані сталі.
де А, В – задані сталі.
- 77 –
 Варіант 3.
Варіант 3.
1.Дано прямокутну мембрану ОАСВ (див. малюнок) зі сторонами ОА=а, ОВ=b. Через сторону ОА підводиться потік тепла 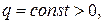 через ОВ тепловий потік такої ж величини відводиться, а на сторонах АС та ВС температура змінюється за законом відповідно
через ОВ тепловий потік такої ж величини відводиться, а на сторонах АС та ВС температура змінюється за законом відповідно 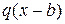 та
та 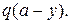 Знайти стаціонарну температуру внутрішніх точок мембрани.
Знайти стаціонарну температуру внутрішніх точок мембрани.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
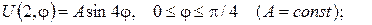

б) 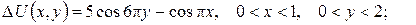
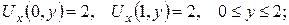
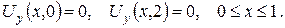
3.За допомогою потенціалу подвійного шару розв’язати зовнішню задачу Діріхле:
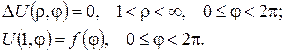
Варіант 4.
1.Знайти положення рівноваги мембрани, яка має форму півкруга радіуса а і знаходиться під дією навантаження, розподіленого згідно закону 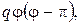 де
де 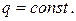 Краї мембрани нерухомо закріплені.
Краї мембрани нерухомо закріплені.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 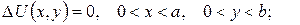
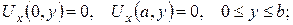
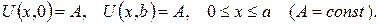
б) 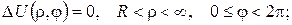
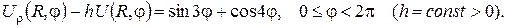
3.За допомогою потенціалу простого шару розв’язати задачу Неймана для півплощини:
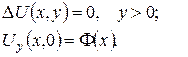
- 78 -
Варіант 5.
1. Дано прямокутну пластинку ОАСВ (див. малюнок до варіанту 3) зі сторонами ОА=а, ОВ=b. Сторони АС та ВС покриті тепловою ізоляцією, а на двох інших підтримується нульова температура. Знайти стаціонарний розподіл температури при умові, що в пластинці виділяється тепло зі сталою інтенсивністю 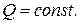
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 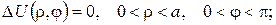
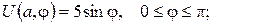
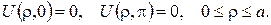
б) 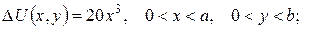
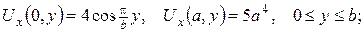
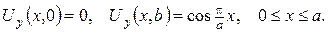
3.Знайти лоґарифмічний потенціал простого шару кола радіуса а зі сталою густиною заряду 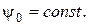
Варіант 6.
1.Визначити стаціонарний розподіл температури в мембрані, яка має форму криволінійного прямокутника, дві сторони якого утворені дугами концентричних кіл 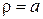 та
та 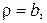 а дві інші – відрізками радіусів
а дві інші – відрізками радіусів 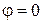 та
та  На краї
На краї 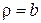 температура змінюється за законом
температура змінюється за законом 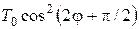
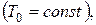 а інші три краї підтримуються при нульовій температурі.
а інші три краї підтримуються при нульовій температурі.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 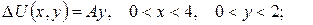
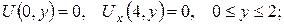
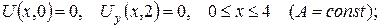
б) 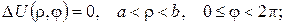
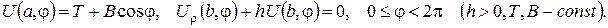
3.За допомогою потенціалу подвійного шару розв’язати задачу Діріхле для півплощини:
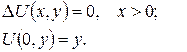
- 79 -
Варіант 7.
1.Тонка плівка натягнута на дротяний каркас, який проектується на площину хОу в прямокутник зі сторонами х=0, х=l , у=0, у=т; відхилення точок контура від площини хОу задається рівностями: 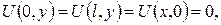
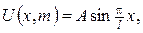 де
де 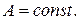 Визначити форму поверхні, по якій розміститься плівка.
Визначити форму поверхні, по якій розміститься плівка.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 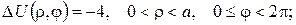
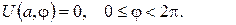
б) 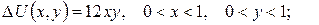
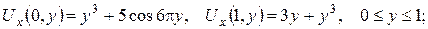

3.Знайти розв’язок задачі Діріхле для рівняння Лапласа зовні кулі одиничного радіуса з центром у початку координат по крайовій умові:
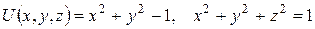
(використати потенціал подвійного шару).
Варіант 8.
1.Знайти стаціонарний розподіл температури всередині нескінченого кругового циліндра радіуса R, якщо на поверхні циліндра підтримується стала температура:
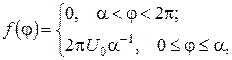
де 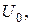 α – задані сталі. Розглянути випадок, коли α досить мале.
α – задані сталі. Розглянути випадок, коли α досить мале.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 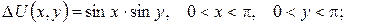
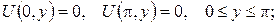

б) 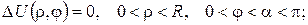
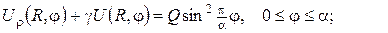
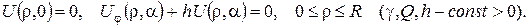
3.Знайти лоґарифмічний потенціал простого шару відрізка 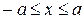 з густиною заряду
з густиною заряду 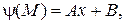 де А, В – задані сталі.
де А, В – задані сталі.
- 80 -
Варіант 9.
1.Знайти стаціонарний розподіл температури всередині прямокутної пластинки, два протилежні краї якої  випромінюють тепло по закону Ньютона в навколишнє середовище нульової температури (коефіцієнт теплообміну h=1), якщо край у=0 підтримується при нульовій температурі, на краї у=b температура змінюється згідно закону
випромінюють тепло по закону Ньютона в навколишнє середовище нульової температури (коефіцієнт теплообміну h=1), якщо край у=0 підтримується при нульовій температурі, на краї у=b температура змінюється згідно закону 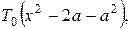 де
де 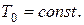
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 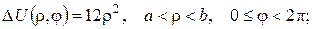
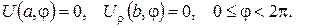
б) 
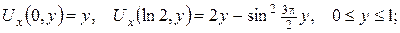
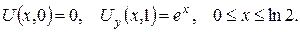
3.Знайти потенціал подвійного шару мас, розподілених по колу одиничного радіуса з центром у початку координат із густиною моментів 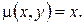
Варіант 10.
1. Тонка плівка натягнута на дротяний каркас, який проектується на площину хОу в круговий сектор 0≤ρ≤R, 0≤φ≤α (0<α<π). На плівку діє навантаження, розподілене згідно закону 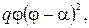 де
де 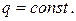 Краї ρ=R та φ=0 нерухомо закріплені, а край φ=α вільний. Визначити форму поверхні, по якій розміститься плівка.
Краї ρ=R та φ=0 нерухомо закріплені, а край φ=α вільний. Визначити форму поверхні, по якій розміститься плівка.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
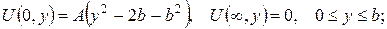
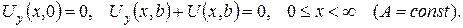
б) 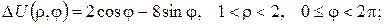
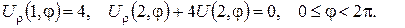
3.Користуючись поверхневими потенціалами, розв’язати задачу Діріхле для півпростору:
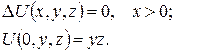
- 81 -
Варіант 11.
1. Визначити форму прогину однорідної прямокутної мембрани зі сторонами а та b, якщо три сторони x=a, y=0, y=b вільні, а на четвертій задане відхилення 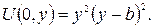
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 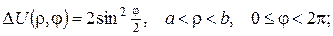
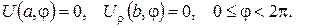
б) 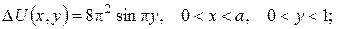
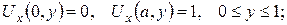
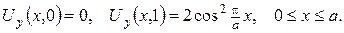
Вказівка. Визначити значення сталої а, при якому дана задача Неймана буде коректно поставленою.
3. Побудувати функцію Ґріна для задачі Діріхле в круговому секторі 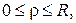
Варіант 12.
1.Напівкругла мембрана радіуса а нерухомо закріплена на півколі й вільна на прямолінійному краї. Знайти форму прогину мембрани під дією рівномірно розподіленого навантаження 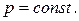
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 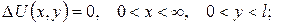
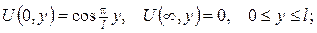
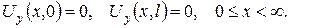
б) 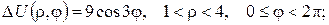
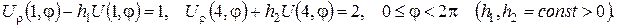
3. Побудувати функцію Ґріна для задачі Діріхле в шарі 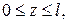
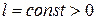 (частина простору, обмежена площинами
(частина простору, обмежена площинами 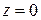 і
і 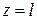 ).
).
- 82 -
Варіант 13.
1. Усередині нескінченого кругового циліндра радіуса 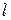 проходить рух нестискуваної рідини. Вважаючи цей рух сталим, потенціальним і плоскопаралельним, знайти закон руху, якщо проекція швидкості
проходить рух нестискуваної рідини. Вважаючи цей рух сталим, потенціальним і плоскопаралельним, знайти закон руху, якщо проекція швидкості 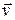 на зовнішню нормаль циліндра в кожній точці задається формулою:
на зовнішню нормаль циліндра в кожній точці задається формулою:
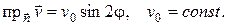
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 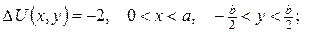
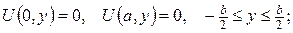
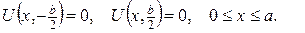
б) 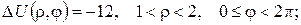
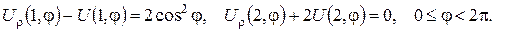
3. За допомогою потенціалу подвійного шару розв’язати задачу Діріхле для півплощини:

Варіант 14.
1.Усередині нескінченого кругового циліндра радіуса 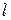 проходить рух нестискуваної рідини. Вважаючи цей рух сталим, потенціальним і плоскопаралельним, знайти закон руху, якщо проекція швидкості
проходить рух нестискуваної рідини. Вважаючи цей рух сталим, потенціальним і плоскопаралельним, знайти закон руху, якщо проекція швидкості 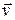 на зовнішню нормаль циліндра в кожній точці задається формулою:
на зовнішню нормаль циліндра в кожній точці задається формулою:

2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 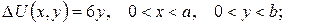
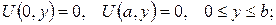
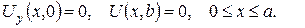
б) 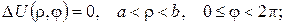
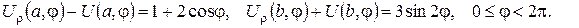
3.За допомогою потенціалу простого шару розв’язати задачу Неймана для півплощини:
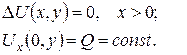
- 83 -
Варіант 15.
1. Знайти стаціонарний розподіл температури в однорідній прямокутній пластинці 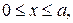
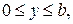 яка підігрівається джерелом тепла, яке виділяє на одиницю площі кількість теплоти
яка підігрівається джерелом тепла, яке виділяє на одиницю площі кількість теплоти 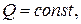 якщо через сторони пластинки тепловіддача в навколишнє середовище нульової температури проходить згідно закону Ньютона.
якщо через сторони пластинки тепловіддача в навколишнє середовище нульової температури проходить згідно закону Ньютона.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 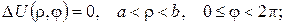
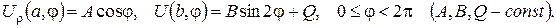
б) 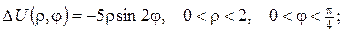


3.Знайти об’ємний потенціал мас, розподілених зі сталою густиною 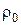 в кубі зі стороною а.
в кубі зі стороною а.
Варіант 16.
1.Знайти розподіл потенціалу електростатичного поля всередині прямокутника ОАСВ (див. малюнок до варіанту 3) зі сторонами ОА=а, ОВ=b, якщо всі сторони прямокутника заземлені, а густина електричних зарядів, розподілених по прямокутнику, рівна 4х-у.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 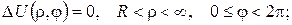
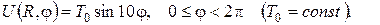
б) 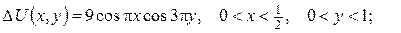
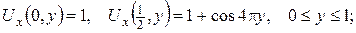
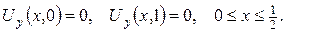
3.Знайти розв’язок задачі Діріхле для рівняння Лапласа в області 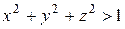 по крайовій умові
по крайовій умові
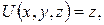
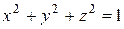
(використати потенціал подвійного шару).
- 84 -
Варіант 17.
1. Знайти закон стаціонарного розподілу температури всередині однорідного нескінченого кругового циліндра радіуса R=4, якщо на його поверхні підтримується температура
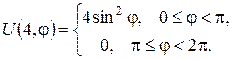
Розв’язок знайти у формі ряду та у формі інтеґрала Пуассона.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
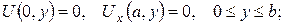
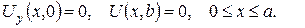
б) 
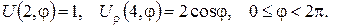
3. Знайти лоґарифмічний потенціал подвійного шару мас, розподілених зі сталою густиною по сторонах прямокутника ОАСВ (ОА=а, ОВ=b; див. малюнок до варіанту 3).
Варіант 18.
1.Дано прямокутну пластинку ОАСВ (ОА=а, ОВ=b). На стороні АС (х=а) підтримується температура Ту, на стороні ВС (у=b) – температура 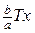
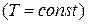 , а на двох інших сторонах – нульова температура. Знайти стаціонарну температуру внутрішніх точок пластинки.
, а на двох інших сторонах – нульова температура. Знайти стаціонарну температуру внутрішніх точок пластинки.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 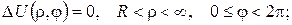
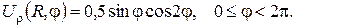
б) 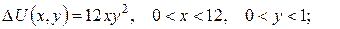
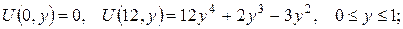
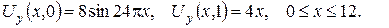
3. Знайти розв’язок задачі Неймана для рівняння Лапласа в крузі радіуса R, користуючись потенціалом простого шару.
- 85 -
Варіант 19.
1.Знайти положення рівноваги мембрани, яка має форму кругового сектора 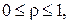
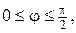 якщо вона знаходиться під навантаженням, розподіленим згідно закону
якщо вона знаходиться під навантаженням, розподіленим згідно закону 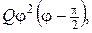 де
де 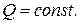 Краї
Краї 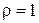 та
та 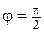 нерухомо закріплені, край
нерухомо закріплені, край 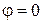 вільний.
вільний.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 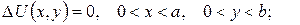
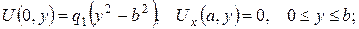
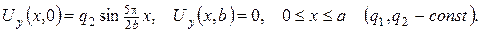
б) 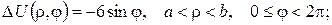
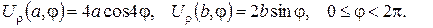
3. Знайти лоґарифмічний потенціал подвійного шару відрізка 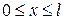 із густиною моментів
із густиною моментів 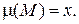
Варіант 20.
1.Знайти форму рівноваги однорідної прямокутної мембрани ОАСВ (див. малюнок до варіанту 3) зі сторонами ОА=а, ОВ=b, закріпленої по краях, якщо до мембрани прикладений нормальний тиск 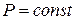 на одиницю площі.
на одиницю площі.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 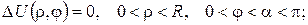

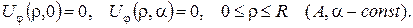
б) 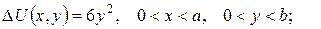
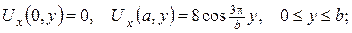
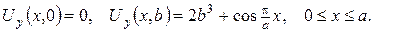
3. Знайти потенціал простого шару мас, розподілених по сфері 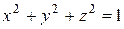 із густиною заряду
із густиною заряду 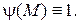
- 86 -
Варіант 21.
1.Визначити стаціонарний розподіл температури в однорідній пластинці, яка має форму криволінійного прямокутника – півкільця, дві сторони якого утворені дугами концентричних кіл радіусів 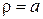 та
та 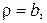 а дві інші – відрізками радіусів
а дві інші – відрізками радіусів 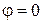 та
та 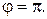 Уздовж ґрані
Уздовж ґрані 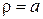 температура змінюється згідно закону
температура змінюється згідно закону 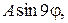 де
де 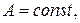 ґрань
ґрань 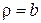 теплоізольована, а інші підтримуться при нульовій температурі.
теплоізольована, а інші підтримуться при нульовій температурі.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 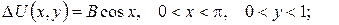
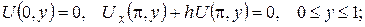

б) 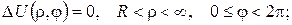
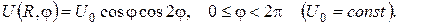
3.Користуючись поверхневими потенціалами, розв’язати другу крайову задачу для рівняння Лапласа в півпросторі:
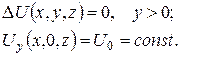
Варіант 22.
1. Знайти стаціонарний розподіл температури в однорідній прямокутній пластинці 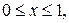
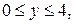 сторони х=0 та х=1 якої теплоізольовані, якщо на
сторони х=0 та х=1 якої теплоізольовані, якщо на
інших сторонах температура задається рівностями: 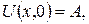
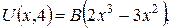 де А, В – задані сталі.
де А, В – задані сталі.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
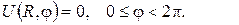
б) 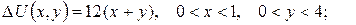
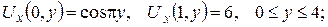
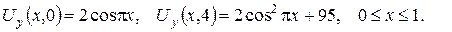
3. Знайти сумарний об’ємний потенціал мас, розподілених усередині кулі радіуса а з центром у початку координат зі сталою густиною  та у сферичному шарі
та у сферичному шарі 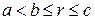
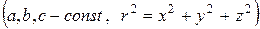 зі сталою густиною
зі сталою густиною 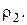
- 87 -
Варіант 23.
1.Визначити форму прогину однорідної круглої мембрани радіуса R, якщо відхилення точок краю мембрани задане функцією 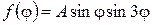
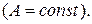
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 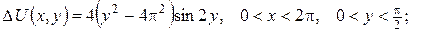
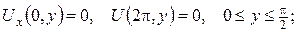
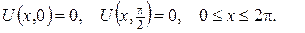
б) 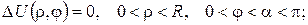
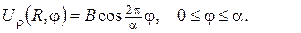
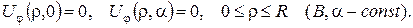
3. Знайти лоґарифмічний потенціал простого шару мас, розподілених зі сталою густиною 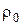 по сторонах квадрата з вершинами в точках (0;0), (0;1), (1;1), (1;0).
по сторонах квадрата з вершинами в точках (0;0), (0;1), (1;1), (1;0).
Варіант 24.
1. Знайти форму рівноваги однорідної прямокутної мембрани 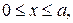
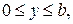 край х=а якої вільний, якщо на інших краях відхилення задане рівностями:
край х=а якої вільний, якщо на інших краях відхилення задане рівностями: 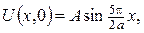
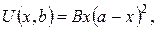
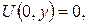 де А, В – задані сталі.
де А, В – задані сталі.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 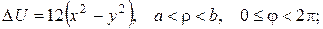
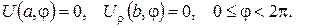
б) 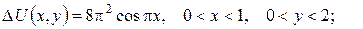
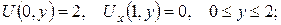
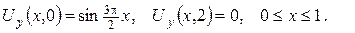
3. Знайти лоґарифмічний потенціал подвійного шару кола радіуса R із центром у початку координат зі сталою густиною моментів 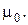
- 88 -
Варіант 25.
1.Знайти стаціонарний розподіл температури в однорідній пластинці, яка має форму кругового сектора 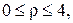
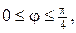 якщо прямолінійні сторони пластинки підтримуються при нульовій температурі, на дузі проходить теплообмін по закону Ньютона з навколишнім середовищем нульової температури, а всередині пластинки діють джерела тепла інтенсивності
якщо прямолінійні сторони пластинки підтримуються при нульовій температурі, на дузі проходить теплообмін по закону Ньютона з навколишнім середовищем нульової температури, а всередині пластинки діють джерела тепла інтенсивності 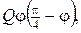 де
де 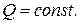
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 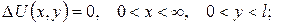
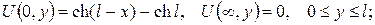
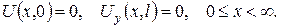
б) 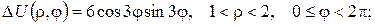
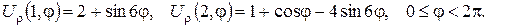
3. Знайти об’ємний потенціал мас, розподілених у кубі з ребром довжини l=2 з густиною 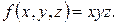
Варіант 26.
1. Знайти стаціонарний розподіл температури в однорідній прямокутній пластинці 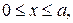
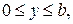 сторона х=0 якої теплоізольована, якщо сторони х=а та у=0 підтримуються при нульовій температурі, а до сторони у=b підводиться тепловий потік
сторона х=0 якої теплоізольована, якщо сторони х=а та у=0 підтримуються при нульовій температурі, а до сторони у=b підводиться тепловий потік  де В – задана стала.
де В – задана стала.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
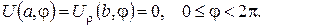
б) 
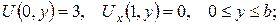
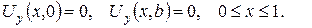
3. Функція 
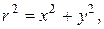 є зовнішнім потенціалом простого шару мас, розподілених по колу
є зовнішнім потенціалом простого шару мас, розподілених по колу 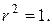 Знайти значення цього потенціалу в крузі
Знайти значення цього потенціалу в крузі 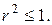
- 89 -
Варіант 27.
1.У напівкруглій пластинці одиничного радіуса прямолінійний край теплоізольований, а на півколі температура задається функцією 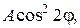 де
де 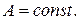 Знайти стаціонарний розподіл температури, якщо в пластинці виділяється тепло з інтенсивністю
Знайти стаціонарний розподіл температури, якщо в пластинці виділяється тепло з інтенсивністю 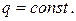
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 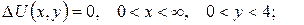
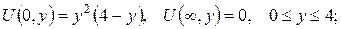
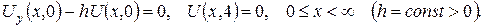
б) 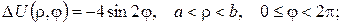
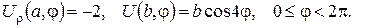
3. Знайти об’ємний потенціал мас, розподілених зі сталою густиною 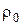 в прямокутному паралелепіпеді
в прямокутному паралелепіпеді 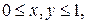
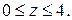
Варіант 28.
1.Знайти стаціонарний розподіл температури в круглій пластинці радіуса R, якщо на краї пластинки проходить теплообмін по закону Ньютона із зовнішнім середовищем, температура якого задана функцією 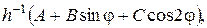 де
де 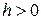 - коефіцієнт теплообміну, а А, В, С – задані сталі.
- коефіцієнт теплообміну, а А, В, С – задані сталі.
2. Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 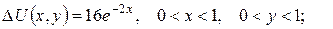

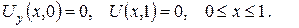
б) 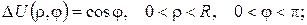
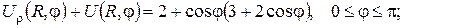
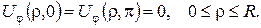
3. Потенціал простого шару мас, розподілених по колу 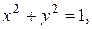 зовні замкнутого круга
зовні замкнутого круга 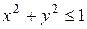 дається формулою:
дається формулою: 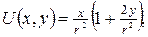
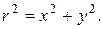 Знайти густину мас
Знайти густину мас 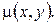
- 90 -
Варіант 29.
1.Знайти стаціонарний розподіл температури в однорідній пластинці, яка має форму кругового сектора 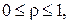
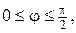 якщо прямолінійні сторони пластинки підтримуються при нульовій температурі, на дузі проходить тепловіддача в навколишнє середовище, температура якого описується функцією
якщо прямолінійні сторони пластинки підтримуються при нульовій температурі, на дузі проходить тепловіддача в навколишнє середовище, температура якого описується функцією  де
де 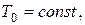 по закону Ньютона.
по закону Ньютона.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 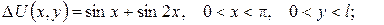
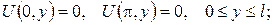
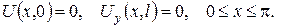
б) 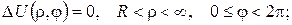

3. Функція 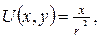
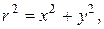 є внутрішнім потенціалом простого шару мас, розподілених по колу
є внутрішнім потенціалом простого шару мас, розподілених по колу 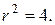 Знайти значення цього потенціалу в крузі
Знайти значення цього потенціалу в крузі 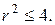
Варіант 30.
1. Визначити форму прогину однорідної прямокутної мембрани 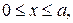
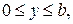 до якої прикладений нормальний тиск
до якої прикладений нормальний тиск 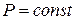 на одиницю площі, якщо сторони мембрани х=0 та х=а вільні, а сторони у=0 та у=b пружно закріплені.
на одиницю площі, якщо сторони мембрани х=0 та х=а вільні, а сторони у=0 та у=b пружно закріплені.
2.Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 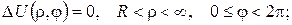
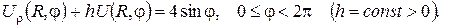
б) 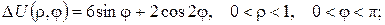
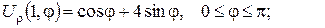
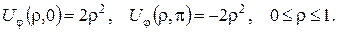
3. Побудувати функцію Ґріна для задачі Діріхле в кільці 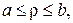
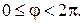
- 91 -
ЛІТЕРАТУРА
1.Петровский И.Г. Лекции об уравнениях с частными производными. – М.: Физматгиз, 1961. – 400 с.
2.Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. – М.: Высшая школа, 1970. – 712 с.
3.Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1966. – 724 с.
4.Перестюк М.О., Маринець В.В. Теорія рівнянь математичної фізики. – К.: Либідь, 2001. – 334 с.
5.Бицадзе А.В., Калиниченко Б.Ф. Сборник задач по уравнениям математической физики. – М.: Наука, 1977. – 224 с.
6.Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. – М.: Наука, 1980. – 668 с.
7.Комеч А.И. Практическое решение уравнений математической физики. – М.: Изд-во МГУ, 1986. – 160 с.
8.Смирнов М.М. Задачи по уравнениям математической физики. – М.: Наука, 1968. – 112 с.
- 92 -
ЗМІСТ
| ТЕМА ІV. РІВНЯННЯ ПАРАБОЛІЧНОГО ТИПУ . . . . . . . . . . . . . . . . . . . . . . | ||
| 1. Постановка змішаних задач для рівнянь параболічного типу . . . . | ||
| 2. Метод відокремлення змінних (метод Фур’є) побудови розв’язку | ||
| змішаних задач для рівнянь параболічного типу . . . . . . . . . . . . . . . | ||
| 3. Задачі Коші для одновимірного рівняння теплопровідності . . . . . | ||
| а) випадок однорідного рівняння . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| б) випадок неоднорідного рівняння . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| 4. Змішані задачі для напівнескінченого стержня з | ||
| теплоізольованою бічною поверхнею . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Контрольні питання . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Завдання для аудиторної роботи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Варіанти індивідуальних завдань до теми ІV . . . . . . . . . . . . . . . . . . . . | ||
| ТЕМА V. РІВНЯННЯ ЕЛІПТИЧНОГО ТИПУ. ТЕОРІЯ ПОТЕНЦІАЛУ . . . . | ||
| 1. Постановка крайових задач для рівнянь еліптичного типу . . . . . . | ||
| 2. Крайові задачі для прямокутних областей. Метод Фур’є. | ||
| Метод власних функцій . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| а) метод Фур’є. Задачі . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| б) метод власних функцій. Задачі . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| 3. Крайові задачі для кругових областей. Метод відокремлення | ||
| змінних. Задачі . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| 4. Функція Ґріна оператора Лапласа . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| 5. Теорія потенціалу. Приклади . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Контрольні питання . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Завдання для аудиторної роботи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Варіанти індивідуальних завдань до теми V . . . . . . . . . . . . . . . . . . . . | ||
| ЛІТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
