X Київський відкритий турнір математичних боїв Тур четвертий

1.На дошці написані ненульових чисел. За один крок дозволяється вибрати з написаних два числа і та записати замість них числа та . Чи можна після декількох кроків повернутися до початкового набору чисел?

Відповідь: не можна.

Розв’язання.Оскільки

.

Тобто після першого кроку сума квадратів усіх записаних чисел збільшується, а далі вже не зменшується.

2.Знайдіть усі натуральні та , для яких справджується рівність:

.

Відповідь: таких чисел не існує.

Розв’язання.Очевидно, що права частина не кратна . Покажемо, що ліва частина ділиться на .

Далі просто перебором варіантів , та переконуємось, що це число завжди кратне .

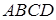3.Заданий квадрат зі стороною 1. На його діагоналі та стороні побудовано рівносторонні трикутники та , як це показане на рис. 1. Знайдіть довжину відрізку .

Відповідь:

Розв’язання. Розглянемо трикутники та . Вони мають однакові пари сторін: , (рис. 1). Крім того , звідки . Тобто у цих трикутників рівний кут між рівними сторонами, тому , звідси .

4.На медіані трикутника позначили такі точки і , що и Доведіть, що

Розв’язання. На промені позначимо точку так, що (рис. 3). Тоді Звідси Крім того, Тоді .

5.Знайдіть усі трійки простих чисел (не обов’язково різних), які задовольняють рівність:

.

Відповідь: , де 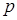– довільне просте число.

Розв’язання.Якщо два з них рівні, то очевидно, що й третє дорівнює першим двом. Таким чином вони попарно різні. Без обмеження загальності можемо вважати, що . Тоді , звідси жодне з цих чисел не може бути рівним , бо з умови випливає, що 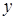– парне. Розкладемо на множники ліву частину заданого рівняння: .Дільниками правої частини є числ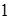а , , , , , , та . Неважко показати, що , тому – парний та менший дільник при розкладі на два множники. Єдиний варіант – це та . Тоді звідки . Тобто одне з чисел – парне, що неможливо.

6.Правильний трикутник зі стороною розрізаний на трикутників зі стороною 1. Скільки існує паралелограмів зі сторонами, що паралельні сторонам великого трикутника?

Відповідь: .

Розв’язання. Очевидно, що паралелограми діляться за трьома напрямами, і кожного напряму з них – рівна кількість. Тому достатньо порахувати кількість одного напряму. Домалюємо ще рядок трикутників, як це показано знизу. Тоді можна вибрати будь-які 4 точки, що розташовані на нижньому добудованому відрізку і їм буде відповідати рівно 1 паралелограм заданого напряму і навпаки (рис. 4). Таким чином є бієкція. Кількість варіантів вибрати 4 вершини на нижньому відрізку – це , тому усього шуканих паралелограмів рівно .

7.Нехай та -- деякі набори дійсних чисел з однаковою сумою. Чи завжди можна побудувати таку таблицю , у якої сума чисел у -му рядку дорівнює , а сума чисел у -му стовпчику дорівнює ?

Відповідь: так, завжди.

Розв’язання. Заповнимо табличку, наприклад, таким чином, як на малюнку справа, де , . Неважко переконатись, що умови виконуються.

,

8.Знайдіть усі трійки послідовних натуральних чисел, для яких сума їх трьох попарних добутків дорівнює , де – деяке натуральне число.

Відповідь: таких чисел не існує.

Розв’язання. Позначимо ці послідовні натуральні числа через , та . Тоді шукана сума трьох попарних добутків дорівнює:

.

Легко зрозуміти, що це число ніколи не ділиться на , а тому не може дорівнювати числу, що кратне .

9.Знайдіть усі натуральні числа , які задовольняють рівність: .

Відповідь: таких чисел не існує

Розв’язання. Якщо 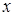– найменше з цих трьох чисел, то , а тому весь вираз завжди більший від .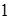

10.Точка лежить на відрізку . Відомо, що , . На прямій вкажіть усі точки , для яких .

Відповідь: точка може знаходитись на відстані 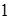по обидва боки від точки .

Розв’язання. Нехай на числовій прямій точки мають координати відповідно. Нехай координата точки дорівнює 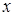. Оскільки , , , то приходимо до рівняння: . З нього знаходимо, що та .

11.У трикутнику 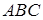з гострим кутом при вершині проведені бісектриса та висота . Відомо, що . Знайдіть величину .

Відповідь: .

Розв’язання. Нехай точка – симетрична точці відносно бісектриси (рис. 5). Тоді точка попадає на відрізок та . Тоді – вписаний, при цьому відрізки , тому дуги описаного навколо кола також рівні, тому , тому вони рівні по , звідси .

12.Знайдіть три останні цифри числа .

Відповідь: .

Розв’язання.Зрозуміло, що роль грають тільки останні три цифри числа. Тому задане число можна переписати такому вигляді:

.

У першій групі 1000 чисел з однаковими останніми трьома цифрами, у другій також, і т.д., у передостанній так само. а у останній усі останні цифри . Таким чином це число ділиться на , а тому має останні цифри .

13.Нехай -- деяка перестановка чисел , при цьому і . Доведіть, що .

Розв’язання. Спочатку побачимо, що для кожного ніколи не може бути одночасно , або . Якщо припустити, наприклад, що , тоді та , тобто елемент не перевищує , що очевидно є суперечністю. Таким чином у кожній різниці завжди є модуль різниці елемента з множини та множини . Тому

.

14.Доведіть, що для усіх натуральних справджується рівність:

.

Розв’язання. Шляхом піднесення до квадрату легко перевірити для усіх натуральних має місце нерівність: , тому для маємо:

.

Покажемо, що . Оскільки для

,

то звідси випливає, що . Тому

.

Тому .

Оскільки між числами та не лежить жоден точний квадрат цілого числа, то твердження доведене.

15.Для довільних додатних чисел розв’яжіть систему рівнянь:

Відповідь: , , .

Розв’язання. Бачимо, що це рівняння лінійне відносно параметрів , то ми можемо їх знайти будь-яким методом. Тоді одержимо, що , , . Далі просто , звідки , а далі знаходимо шукані невідомі: , , .

16.У трикутнику 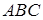сторони задовольняють умову . Позначимо через – півпериметр та через – площу 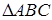. Доведіть, що 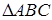– прямокутний тоді і тільки тоді, коли .

Розв’язання. Запишемо такі рівносильні перетворення:

.

Якщо трикутник прямокутний, то з останньої умови маємо, що і .

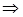
Якщо , оскільки при – спадає, то єдиним шуканим значенням є .

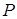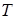17. З точки до кола проведені дві дотичні та , . Нехай – діаметр кола, точка – основа перпендикуляра, проведеного з точки 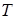на діаметр . Доведіть, що ділить навпіл відрізок .

Розв’язання. На прямій будуємо таку точку , що , тоді і на прямій лежить середня лінія , тому ділить навпіл (рис. 6). Тому -- паралелограм, звідки також ділиться навпіл прямою , а далі з міркувань подібності й також ділиться навпіл, що й треба було довести.

18.Коефіцієнти квадратного рівняння є степенями двійки. Доведіть, що якщо його корені цілі числа, то вони співпадають.

Розв’язання.З теореми Вієта значення та – цілі числа. Тому можна скоротити на і розглянути зведене квадратне рівняння . Його коефіцієнти невід’ємні степені , нехай , . Оскільки добуток коренів – степінь , то кожен з них або додатна степінь або 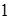. Нехай – корінь, тоді . Поділимо цю рівність на найменшу степінь , тоді одержимо рівність , де принаймні одне з чисел 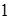, а інші – невід’ємні степені . Це можливо лише за умови, якщо , . Тому , . Звідси , що й треба було довести.

19.Доведіть, що існує нескінченно багато натуральних чисел вигляду , які мають пару дільників, різниця між якими дорівнює .

Розв’язання. Покажемо, що існує нескінченно багато таких натуральних , що рівняння має розв’язок для деякого натурального 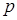. Перепишемо це рівняння у такому вигляді: . Звідси

.

Таким чином число повинно бути повним квадратом, тоді шукане 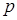буде натуральним. Побудуємо нескінченну послідовність таких значень для . Бачимо, що . Нехай тепер натуральні такі, що . Тоді зрозуміло, що та ці числа однієї парності. Тоді натуральне число при цьому

.

Зрозуміло, що число -- натуральне, а тому ми починаючи з будується шукана послідовність чисел.

20.Розглядаємо усі підмножини множини , які не містять послідовних натуральних чисел, та обчислюємо для них добуток усіх елементів. Чому дорівнює сума квадратів цих добутків? Вважаємо за означенням, що порожня множина має добуток елементів, що дорівнює 1.

Відповідь: .

Розв’язання. Позначимо відповідну суму квадратів добутків елементів через . Для (узагальнимо на цей приклад задачу також) маємо, що , бо тут тільки порожня множина існує. Для маємо дві множини, для яких . Так само не важко пересвідчитись, що . Припустимо, що .

Доведемо це ММІ. База вже перевірена. Значення одержується таким чином: беруться умі множини з попереднього кроку, що не містять елемент , а також усі множини з кроку з додаванням елементу , звідки одержимо таку рекурентну формулу:

,

з якої за припущенням індукції маємо шукане значення:

,

що й треба було довести.

21.Дві команди грають у хокей доки одна з команд не заб’є 10 голів. У протокол вносять записи після кожного забитого гола, наприклад, 0-0, 0-1, 0-2, 1-2, ..., 5-10. Скільки усього різних протоколів може вийти?

Відповідь: .

Розв’язання. Допишемо протокол до рахунку 10-10. Зрозуміло, що між такими протоколами та справжніми є бієкція, тобто їх кількість однакова. Залишається зрозуміти, що усього таких є .

22.У опуклому чотирикутнику 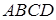точка 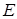– середина 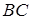, . Доведіть, що .

Розв’язання. Нехай точка 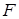– центрально симетрична точці 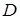відносно точки 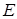(рис. 7). Тоді , тому . Тепер запишемо:

.

З іншого боку, , тому . Тому , звідки випливає, що , тому , що й треба було довести.

23.Маємо рівняння . Знайдіть суму , де – дійсні корені цього рівняння.

Відповідь: .

Розв’язання. Розв’язання базується на формулі

, де .

Якщо її узагальнити, то можна одержати таку формулу:

, де

, , .

Залишається переконатись, що рівняння має 4 корені , та виконується мова , де , , та .

Оскільки , та , то маємо 4 зміни знаку неперервної функції, що відповідає наявності рівно 4-х корнів.

24.Для дійсних чисел доведіть нерівність:

.

Розв’язання. Позначимо через , та , тоді зі відомої нерівності маємо:

,

що й треба було довести.

25.Нехай - просте , та - цілі числа такі, що . Доведіть, що

.

Розв’язання.Доведення: Якщо обидва числа кратні , то твердження очевидне. Тому надалі можемо вважати, що вони обидва взаємно прості з . Тоді, існує , що , тоді Позначимо , тоді . Також, подільність рівносильна подільності , бо .

Доведемо, що існує многочлен з цілими коефіцієнтами, що

.

Маємо, всі коефіцієнти діляться на , бо рівні . Тому достатньо довести, що . Нехай - корінь рівняння . Тоді достатньо довести, що - корінь та . Маємо, та тоді, враховуючи , та

Таким чином, , звідки і випливає твердження задачі.