Распределение напряжений в случае плоской задачи при действии равномерно

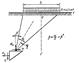σ_z = P*(α+sinα*cos2β)/π = P*K_z

σ_y = P*(α-sinα*cos2β)/ π = P*K_y

τ = P*(sinα*cos2β)/ π = P*K_yz

K=f(z/b, y/b)

Использую табл. и фор-лы можно построить эпюры напряжений по

Главные напряжения,т.е. наибольшие и наименьшие нормаль­ные напряжения, будут для площадок, расположенных по вертикаль­ной оси симметрии нагрузки. Действительно, для таких площадокугол β' = -α/2и, след-но, угол β = α/2 - α/2 = 0.

Тогда сдвигающее напря­жение будет равно τ = 0, т. е. площадки будут главными.

Можно показать, что главными площадками будут также площадки, расположенные по биссектрисам углов видимости и площадкам, им перпендикулярным.

Величину главных напряжений, полагая в них β = 0:

σ₁ = P*(α+sinα)/π

σ₂ = P*(α-sinα)/ π

Эти формулы весьма часто применяют при оценке напряжен­ного состояния в основаниях сооружений, особенно предельного.

Они дают также возможность построить эллипсы напряжений для различных точек напряженного линейно деформируемого полупрост­ранства,наглядно иллюстрирующих изменение напряже­ний в грунте под полосообразной нагрузкой.

КОНТАКТНАЯ ЗАДАЧА.

Вопрос о распределении давлений по подошве сооружений имеет большое практическое значение, особенно для гибких фундаментов, рассчитываемых на изгиб. Если известно реактивное давление по подошве фундамента, которое обычно называют контактным, то, приложив к подошве фундаментной балки его обратную величину, находят величину расчетных изгибающих моментов и перерезывающих сил, применяя обычные уравнения статики. Большинство фундаментов сооружений обладает определенной жесткостью. Поэтому важно оценить, как жесткость фундамента сказывается на распределении контактных давлений и давлений в массиве грунта. Уравнением для решения задачи явл-ся формула Буссинеска для верт-ой деформации линейно деформируемого полупространства от действия сосредоточенной силы: w_z=p/(πC_oR). Если фундамент абсолютно жесткий, то все точки его площади подошвы будут иметь при центральной нагрузке одну и ту же верт-ую деф-ию.
Таким образом, условие абсолютной жесткости фундамента: w_z= const.

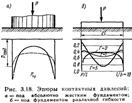
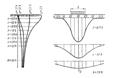
Если начертить эпюру контактных давлений (рис.1), то для абсолютно жесткого фунд. на линейно деф-ом полупространстве будем иметь седлоообразную эпюру с бесконечно большими давлениями по краям.
Однако, как показывают решения, выполненные с учетом ползучести скелета грунта и одновременно с возрастанием по глубине модуля общей деф-ии,контактные давления по подошве жесткого фунд. будут распр-ся по более пологой кривой и, кроме того, у края фунд. они не могут быть больше предела несущей спос-ти грунта, что также обусловливает перераспр-е давлений по подошве (рис.1, пунктирная линия).

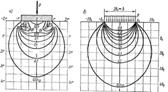
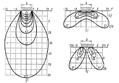
Рис. 2. Изобары в грунте под фундаментами абсолютно жестким (а) и гибким (б)

На рис. 2 изобары для фундаментов абсолютно жесткого и абсолютно гибкого, которые подтверждают сказанное выше. Для подошвы фундаментов эпюра контактных давлений по решениям, излагаемым в курсе сопр-ия материалов, будет прямолинейной — равномерной или трапецеидальной, тогда как по строгому решению теории упругости для абсолютно жестких фундаментов она всегда будет седлообразной; для фундаментов же конечной жесткости эпюра может принимать очертания от седлообразного до параболического (см. рис. 2,б).
Распределение контактных давлений по подошве фундаментов зависит не только от гибкости фунд., но и от глубины их заложения, величины внешней нагрузки, обусловливающей развитие пластических деф-й в грунте, а след-но, и от прочностных св-в гр.

22.Распределение сжимающих напряжений в слое грунта ограниченной толщины на несжимаемом основании вслучае гибкой полосообразной равномерно распределенной нагрузки было получено (на основе задачи Маргера и Шехтер) в Институте оснований, рез-ты выч-ий сведены в таблицу.

По данным этой таблицы на рис. 1 построены эпюры распределения сжимающих напряжений по оси полосообразной нагрузки для случаев залегания несжимаемой скальной породы на глубине, равной полуширине (1), ширине (1’) и 2,5 ширины (1”) ленточной нагрузки. На этом же рисунке показана эпюра 2 максимальных сжимающих напряжений для случаев однородного полупространства (без наличия скального подстилающего слоя) и распределение тех же напряжений 3, 3’, 3” в случае более неодн-го подстилающего слоя с переменным модулем деформ-сти, когда он на нижней границе слоя в несколько раз меньше модуля деформ-сти у подошвы нагрузки.

Рис. 1. Эпюры распр-я макс. сжим-щих напр-й под центром гибкой равномерно нагруженной полосы в слое грунта огранич-й толщины b₁, 2b₁ и 5 b₁: 1- при наличии подстилающей несжим. породы; 2—для однородного полупространства; 3 — для неоднородного слоя с возрастающей по глубине сжим-тью грунта.

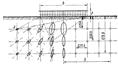
Из рассмотрения эпюр распределения сжимающихся напр-й (давлений) вытекает, что наличие жесткого несжим-го слоя вызыв. концентрацию(возраст) напр-й по оси нагрузки, тогда как увеличение сжимаемости грунта с глубиной уменьшает концентрацию напряжений. Распред. контактных давлений для слоя грунта ограниченнлой толщины, опирающегося на несжим. основание, для жестк. фунд опред-ся по таблицам. Для фунд. гибких – таблица для определения контактных давлений на слой грунта ограниченной толщины под действием полосообразной нагрузки интенсивностью р, при допущении отсутствия трения по контакту упругого слоя с несжимаемым основанием по методу ступенчатого суммирования (рис. 2).
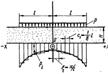Рис. 2 Эпюра реактивных давлений реактивных давлений по подошве гибкого фундамента при слое грунта ограниченной толщины.

В таблице значения даны для пяти различных мощностей слоя грунта ограниченной толщины в зависимости от гибкости фундаментной балки.