Нелинейном преобразовании

Для решения задачи определения погрешно­сти измеряемой величины y, связанной с влияющей величиной x нелиней­ной функцией преобразова­ния

, (Б.1)

необходимо по известной функции рас­пределения 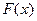и выражению (Б.1) найти функцию распределения .

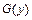По определению интегральной функции распределения

.

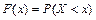Очевидно, что для монотонно возрастающей функции преобразования

.

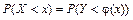Поскольку по определению

,

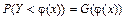то

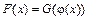. (Б.2)

Производя обратное преобразование выражения (Б.1), получаем

,

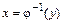тогда

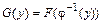. (Б.3)

Дифференцируя выражение (Б.3), получаем дифференциальную функцию распределения частной погрешности y:

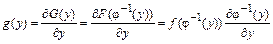. (Б.4)

При нахождении доверительных границ частной погреш­ности y, их можно получить для той же самой доверительной вероятно­сти P_д из границ изменения влияющей величины x a и b:

xÎ[a;b], P_д,

yÎ[j(a); j(b)], P_д,

где P_д=F(b)-F(a)=G [j(b)]-G[ j(a)].

Графическое решение задачи трансформации законов распределе­ния приведено на рисунке Б.1. Этот способ трансформации удобен в том случае, когда аналитическое решение затруднительно или исходное рас­пределение 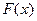получено экспериментальным путем.

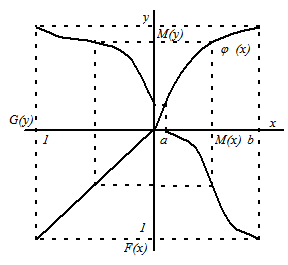Рисунок Б.1 – Графическая интерпретация трансформации

закона распределения

Рассмотрим несколько случаев трансформации законов распреде­лений.

1. Линейная функция преобразования .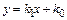

Произведем обратное преобразование 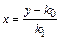, тогда по формуле (Б.3) имеем .

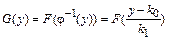Таким образом, при линейном преобразовании функция распределе­ния не изменяется, а лишь сдвигается по оси абсцисс на 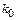и претерпевает ком­прессию (декомпрессию) в 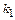раз.

2. Квадратическая функция распределения .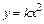

Рассмотрим преобразование величины x, имеющей равномерное рас­преде­ление

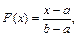
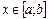. (Б.5)

Обратное преобразование 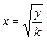. По формуле (Б.3) функция распределения величины y имеет вид

,

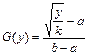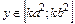
Если влияющая величина x имеет нормальное распределение с функ­цией распределения

,

то при трансформации с квадратичной функцией преобразования функция распределения преобразуется к виду

.

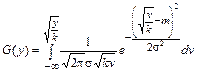Дифференциальная функция распределения при этом

.

3. Функция преобразования вида .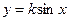

Этот случай встречается при оценивании погрешности рассогласова­ния при измерении мощности на СВЧ. По такому закону изменяется по­грешность рассогласования в зависимости от фазы коэффициента отраже­ния. Величина фазы детерминирована, но неизвестна, поэтому для отыска­ния погрешности рассогласования предполагают, что все значения фазы распределены по равновероятному закону, функция рас­пределения которого имеет вид (Б.5). Необходимо определить, по какому закону распределена погрешность рассогласования.

Выполним обратное преобразование функции преобразования

.

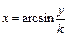Тогда выражение для функция распределения погрешности рассогласования согласно формуле (Б.3) запишется следующим образом

, .

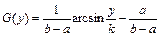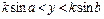Обычно фаза коэффициента отражения изменяется в пределах 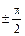, то есть 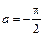, , 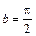тогда выражение (Б.5) преобразу­ется к виду

, .

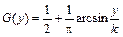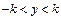Из последнего выражения видно, что погрешность рассогласова­ния распределена по закону арксинуса.

СПИСОК ЛИТЕРАТУРЫ

1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов.- М.: Наука, 1981. - 721 с.

2. Бурдун Г.Д. , Марков Б.Н. Основы метрологии. – М.: Изд-во стандартов, 1985. – 286 с.

3. Грановский В.А., Сирая Т.Н. Методы обработки экспериментальных данных при измерениях. – М.: Энергоатомиздат, 1990.– 288 с.

4. Земельман М.А. Метрологические основы технических измерений. – М.: Изд-во стандартов, 1991.- 228 с.

5. Закон України про метрологію та метрологічну діяльність. – К.: Держстандарт України, 1998. – 20 с.

6. Кузнецов В.А., Ялунина Г.В. Метрология (теоретические, прикладные и законодательные основы): Учеб. пособие. – М: ИПК Издательство стандартов, 1998. – 336 с.

7. Кукуш В.Д. Определение погрешностей результатов и средств измерений. – Харьков: ХПИ, 1979. – 116 с.

8. Кукуш В.Д. Электрорадиоизмерения. – Л.: Энергоатомиздат, 1983. – 367 с.

9. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л.: Энергоатомиздат, 1985. – 248 с.

10. Орнатский П.П. Теоретические основы информационно-измерительной техники. – Киев.: Вища школа, 1983. – 455 с.

11. Рабинович С.Г. Погрешности измерений. – Энергия, 1978.- 262 с.

12. Шишкин И.Ф. Теоретическая метрология. – М.: Изд-во стандартов, 1991. – 492 с.

13. Фильчаков П.Ф. Численные и графические методы прикладной математики: Справочник. – Киев.: Наук. Думка, 1970. – 800 с.