Или пространственному изгибу
Основные определения
 Рис. 5.3. Косой изгиб Рис. 5.3. Косой изгиб |
 Рис. 5.4. Пространственный изгиб Рис. 5.4. Пространственный изгиб |
Косым изгибом называется такой изгиб, при котором вся нагрузка на балку действует в одной плоскости и эта плоскость не совпадает с плоскостями, в которых лежат главные центральные оси инерции сечения (плоскости  и
и  на рис. 5.3). При косом изгибе изогнутая ось представляет собой плоскую кривую и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки. При пространственном изгибе нагрузка приложена в разных плоскостях (рис. 5.4), деформированная ось является пространственной кривой.
на рис. 5.3). При косом изгибе изогнутая ось представляет собой плоскую кривую и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки. При пространственном изгибе нагрузка приложена в разных плоскостях (рис. 5.4), деформированная ось является пространственной кривой.
При косом или пространственном изгибе в сечении стержня возникают четыре усилия: 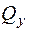 ,
, 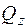 ,
, 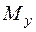 и
и 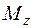 . Нормальные напряжения в произвольной точке сечения определяются по формуле, полученной из (5.1) при
. Нормальные напряжения в произвольной точке сечения определяются по формуле, полученной из (5.1) при  ,
,
 . (5.3)
. (5.3)
Касательные напряжения от поперечных сил, если нельзя воспользоваться формулой Журавского, допустимо не учитывать.
Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе. Для этого необходимо:
· построить эпюры внутренних усилий[2]. Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие. Вертикальная составляющая вызывает изгиб относительно горизонтальной оси 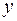 , горизонтальная – относительно оси
, горизонтальная – относительно оси 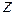 ;
;
· выбрать опасные сечения – сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;
· в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;
· записать условие прочности в этих точках. Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.
Определение положения опасных точек в стержне произвольного поперечного сечения производится по схеме, описанной ранее во вступительной части разд. 5. Поскольку в уравнении нейтральной линии
 (5.4)
(5.4)
отсутствует свободный член, то нейтральная линия проходит через центр тяжести сечения (рис. 5.5). Построив нейтральную линию и эпюру нормальных напряжений, найдем положение опасных точек. Допустим, что напряжение в точке 1 больше, чем в точке 1¢ (это можно определить по масштабу, если построить сечение и эпюру напряжений в масштабе). Условие прочности в опасной точке 1, которая находится в линейном напряженном состоянии, записывается так:
 . (5.5)
. (5.5)
Значение  зависит от материала, из которого сделана балка, и для хрупкого материала необходимо учесть направление (растягивающее или сжимающее)
зависит от материала, из которого сделана балка, и для хрупкого материала необходимо учесть направление (растягивающее или сжимающее)  .
.
Для некоторых форм сечений, а именно прямоугольника, двутавра и других сечений, угловые точки которых находятся в углах прямоугольника, нет необходимости для записи условий прочности находить положение опасных точек. Для таких сечений положение опасных точек не зависит от угла наклона нейтральной линии, и опасные точки – это всегда угловые точки сечения. Условие прочности в этих точках записывается следующим образом:
 , (5.6)
, (5.6)
где  и
и  – моменты сопротивления поперечного сечения относительно главных центральных осей.
– моменты сопротивления поперечного сечения относительно главных центральных осей.
 Рис. 5.5. Эпюра нормальных напряжений и перемещение точки О оси балки Рис. 5.5. Эпюра нормальных напряжений и перемещение точки О оси балки |
Перемещения балки, работающей в условиях косого или пространственного изгиба, можно находить любым способом. Обычно это делают методом Максвелла – Мора, перемножая эпюры с помощью правила Верещагина. От вертикальной составляющей нагрузки точки оси балки перемещаются по вертикали (вдоль оси 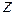 ). Вертикальная составляющая полного прогиба
). Вертикальная составляющая полного прогиба  находится по формуле
находится по формуле
 . (5.7)
. (5.7)
Перемещения  точек оси балки вдоль оси
точек оси балки вдоль оси 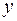 , вызванные горизонтальной составляющей нагрузки, определяются аналогично:
, вызванные горизонтальной составляющей нагрузки, определяются аналогично:
 . (5.8)
. (5.8)
Эти перемещения для точки  оси балки показаны на рис. 5.5. Полное перемещение (отрезок
оси балки показаны на рис. 5.5. Полное перемещение (отрезок  на рис. 5.5) является геометрической суммой составляющих
на рис. 5.5) является геометрической суммой составляющих  и
и  . Отметим такую закономерность: при косом изгибе отрезок
. Отметим такую закономерность: при косом изгибе отрезок  должен быть в точности перпендикулярен нейтральной линии [2], при пространственном изгибе этот угол, как правило, должен быть близок к
должен быть в точности перпендикулярен нейтральной линии [2], при пространственном изгибе этот угол, как правило, должен быть близок к  . При косом изгибе плоскость, в которой лежит изогнутая ось стержня, не совпадает с плоскостью действия нагрузки. Это отличает косой изгиб от прямого, при котором плоскость действия нагрузки совпадает с одной из главных плоскостей осей инерции сечения и изогнутая ось лежит в той же плоскости.
. При косом изгибе плоскость, в которой лежит изогнутая ось стержня, не совпадает с плоскостью действия нагрузки. Это отличает косой изгиб от прямого, при котором плоскость действия нагрузки совпадает с одной из главных плоскостей осей инерции сечения и изогнутая ось лежит в той же плоскости.
Пример расчета балки при пространственном изгибе (задача № 28)
Условие задачи
Балка загружена нагрузкой, показанной на рис. 5.6. Сила  кН действует в вертикальной плоскости,
кН действует в вертикальной плоскости,  кН – в горизонтальной, пара сил
кН – в горизонтальной, пара сил  кН×м – в плоскости, расположенной под углом
кН×м – в плоскости, расположенной под углом  к оси
к оси 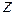 .
.
Требуется:
1) из условия прочности подобрать номер двутавра;
 Рис. 5.6. Схема нагрузки на балку Рис. 5.6. Схема нагрузки на балку |
2) найти полное перемещение точки  оси балки (см. рис. 5.6);
оси балки (см. рис. 5.6);
3) нарисовать сечение балки в масштабе и показать на нем нейтральную линию и полное перемещение точки  . Определить угол между нейтральной линией и полным перемещением[3].
. Определить угол между нейтральной линией и полным перемещением[3].
Решение
Разложим нагрузку на вертикальную (рис. 5.7, а) и горизонтальную (рис. 5.7, в) составляющие и построим эпюры 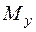 и
и 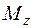 (рис. 5.7, б, г). Чтобы правильно поставить знаки изгибающих моментов, необходимо на рисунках показывать направление осей
(рис. 5.7, б, г). Чтобы правильно поставить знаки изгибающих моментов, необходимо на рисунках показывать направление осей 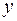 и
и 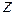 , так как в соответствии с правилом знаков для изгибающего момента в задачах сложного сопротивления знак момента зависит от направления осей. Эпюры моментов строим со стороны растянутых волокон в той плоскости, в которой действует нагрузка. По эпюрам выбираем опасные сечения. В рассматриваемом примере их два: сечение
, так как в соответствии с правилом знаков для изгибающего момента в задачах сложного сопротивления знак момента зависит от направления осей. Эпюры моментов строим со стороны растянутых волокон в той плоскости, в которой действует нагрузка. По эпюрам выбираем опасные сечения. В рассматриваемом примере их два: сечение  , в котором действуют
, в котором действуют  кН×м и
кН×м и  кН×м, и сечение
кН×м, и сечение  с изгибающими моментами
с изгибающими моментами  кН×м и
кН×м и  кН×м.
кН×м.
Условие прочности в опасных точках двутавра имеет вид (5.6). Поскольку отношение моментов сопротивления  зависит от номера двутавра, а он неизвестен, примем это отношение условно[4] равным 10.
зависит от номера двутавра, а он неизвестен, примем это отношение условно[4] равным 10.
 Рис. 5.7. Эпюры изгибающих моментов: а, б – от вертикальной составляющей нагрузки; в, г – от горизонтальной составляющей нагрузки; д, е – от единичной силы Рис. 5.7. Эпюры изгибающих моментов: а, б – от вертикальной составляющей нагрузки; в, г – от горизонтальной составляющей нагрузки; д, е – от единичной силы |
Тогда условие прочности (5.6) в опасных точках сечения  примет вид
примет вид
 ,
,
где допускаемое напряжение для стали принято  = 160 МПа; величины изгибающих моментов переведены из кН×м в кН×см. Из написанного условия прочности найдем необходимый момент сопротивления
= 160 МПа; величины изгибающих моментов переведены из кН×м в кН×см. Из написанного условия прочности найдем необходимый момент сопротивления
 см3.
см3.
По сортаменту прокатной стали подбираем номер двутавра. Для двутавра № 50 с такими характеристиками:  см3 и
см3 и  см3 условие прочности в опасных точках сечения
см3 условие прочности в опасных точках сечения 
 кН/см2
кН/см2
не выполняется, поэтому увеличиваем двутавр. Проверим прочность для двутавра № 55, у которого  см3 и
см3 и  см3:
см3:
 кН/см2.
кН/см2.
Убедимся в том, что условие прочности выполняется и в опасных точках опасного сечения  :
:
 кН/см2.
кН/см2.
Обратите внимание на величину напряжений от изгибающего момента 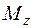 , действующего в горизонтальной плоскости, которую показывает второй член в сумме. Видно, что, несмотря на то, что
, действующего в горизонтальной плоскости, которую показывает второй член в сумме. Видно, что, несмотря на то, что 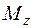 в рассмотренном примере существенно меньше
в рассмотренном примере существенно меньше 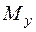 , напряжения от
, напряжения от 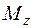 больше, чем напряжения от
больше, чем напряжения от 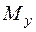 (или они примерно одинаковы). Это говорит об опасности изгиба в горизонтальной плоскости, особенно для двутавров, у которых
(или они примерно одинаковы). Это говорит об опасности изгиба в горизонтальной плоскости, особенно для двутавров, у которых  .
.
Найдем перемещение точки  . Будем искать по формуле (5.7) сначала вертикальную составляющую перемещения, вызванную вертикальной составляющей нагрузки. Формулу Максвелла – Мора (5.7) интегрируем по правилу Верещагина, перемножая эпюры
. Будем искать по формуле (5.7) сначала вертикальную составляющую перемещения, вызванную вертикальной составляющей нагрузки. Формулу Максвелла – Мора (5.7) интегрируем по правилу Верещагина, перемножая эпюры 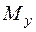 и
и 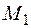 (рис. 5.7, б, е). Если хотя бы одна эпюра на участке имеет форму трапеции, используем для перемножения правило трапеций [6].
(рис. 5.7, б, е). Если хотя бы одна эпюра на участке имеет форму трапеции, используем для перемножения правило трапеций [6].

 кН×м3.
кН×м3.
Аналогично определим по (5.8) горизонтальную составляющую перемещения[5], перемножая эпюры 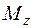 и
и 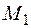 (рис. 5.7, г, е).
(рис. 5.7, г, е).
 кН×м3.
кН×м3.
Положительные знаки перемещений свидетельствуют о том, что перемещения происходят по направлениям единичных сил, т. е. вертикальное перемещение – вниз (по направлению оси 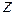 ), горизонтальное – по направлению оси
), горизонтальное – по направлению оси 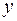 . Сосчитаем найденные составляющие перемещения (в см), разделив их на соответствующие жесткости.
. Сосчитаем найденные составляющие перемещения (в см), разделив их на соответствующие жесткости.
 кН×см2,
кН×см2,
 кН×см2,
кН×см2,
 см,
см,
 см.
см.
Из сравнения величин  и
и  видно, что горизонтальная составляющая перемещения, даже при небольшой горизонтальной нагрузке, много больше (особенно для двутавра) вертикальной составляющей.
видно, что горизонтальная составляющая перемещения, даже при небольшой горизонтальной нагрузке, много больше (особенно для двутавра) вертикальной составляющей.
Выполним последнюю часть задачи. Нарисуем сечение балки в масштабе, покажем на нем нейтральную линию и полное перемещение. Уравнение нейтральной линии (5.4) в опасном сечении С имеет вид[6]

или  . Нейтральная линия, построенная по этому уравнению, и эпюра нормальных напряжений в сечении
. Нейтральная линия, построенная по этому уравнению, и эпюра нормальных напряжений в сечении  показаны на рис. 5.8. Знаки напряжений соответствуют положительным знакам изгибающих моментов. Угловые точки 1, 1¢ – это опасные точки сечения, в которых мы ранее находили напряжения.
показаны на рис. 5.8. Знаки напряжений соответствуют положительным знакам изгибающих моментов. Угловые точки 1, 1¢ – это опасные точки сечения, в которых мы ранее находили напряжения.
 Рис. 5.8. Эпюра напряжений в опасном сечении С и перемещение точки С Рис. 5.8. Эпюра напряжений в опасном сечении С и перемещение точки С |
Найдем угол 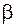 (см. рис. 5.8) между нейтральной линией и осью
(см. рис. 5.8) между нейтральной линией и осью 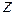 :
:

 .
.
Отложим в масштабе найденные ранее вертикальную  и горизонтальную
и горизонтальную  составляющие перемещения с учетом их направления. Полное перемещение точки
составляющие перемещения с учетом их направления. Полное перемещение точки  – отрезок
– отрезок  на рис. 5.8 равен геометрической сумме
на рис. 5.8 равен геометрической сумме  и
и  . Угол
. Угол 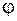 между полным перемещением и осью
между полным перемещением и осью 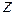

 .
.
Таким образом, угол между полным перемещением  и нейтральной линией
и нейтральной линией  , что близко к
, что близко к  .
.
