Статистическая гипотеза о генеральной средней
Пусть исследуется некоторый признак Х генеральной совокупности. Предположим, что он распределен по нормальному закону. Генеральная средняя 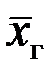 неизвестна, однако есть основания предположить, что она равна некоторому числу а0. Возьмем, например, в качестве генеральной совокупности множество всех студентов и курсантов первого курса высших учебных заведений России, а значение признака Х будет определять количество секунд, необходимых учащемуся для пробега дистанции в 100 метров. В этом случае за величину а0 может быть принят средний норматив бега на 100 метров для лиц соответствующего возраста.
неизвестна, однако есть основания предположить, что она равна некоторому числу а0. Возьмем, например, в качестве генеральной совокупности множество всех студентов и курсантов первого курса высших учебных заведений России, а значение признака Х будет определять количество секунд, необходимых учащемуся для пробега дистанции в 100 метров. В этом случае за величину а0 может быть принят средний норматив бега на 100 метров для лиц соответствующего возраста.
Итак, необходимо проверить гипотезу о том, что генеральная средняя равна некоторому определенному числу. С подобного рода задачами, кроме вышеприведенной о среднем нормативе, встречаются при проверке качества продукции, характеризуемого средним показателем: средней эффективностью, средней продолжительностью работы и т.д.
При проверке гипотезы о генеральной средней необходимо различать два возможных варианта:
I. Стандартное отклонение 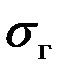 генеральной совокупности известно (найдено теоретически или вычислено по выборке большого объема, полученной при рассмотрении аналогичной задачи, – в этом случае получается достаточно хорошая оценка для дисперсии).
генеральной совокупности известно (найдено теоретически или вычислено по выборке большого объема, полученной при рассмотрении аналогичной задачи, – в этом случае получается достаточно хорошая оценка для дисперсии).
II. Стандартное отклонение 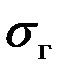 генеральной совокупности неизвестно.
генеральной совокупности неизвестно.
Для каждого из этих вариантов для проверки гипотезы имеется свой критерий, а также свои формулы и правила для определения выборочного значения критерия и критических точек.
I. 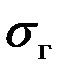 - известно.
- известно.
Обратимся к общей схеме и конкретизируем каждый ее пункт для рассматриваемой гипотезы.
1. Формулируется основная гипотеза 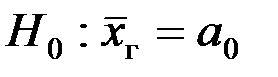 и одна из альтернативных
и одна из альтернативных 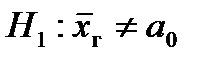 или
или 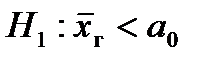 или
или 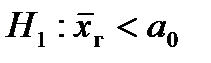 .
.
2. Выбирается уровень значимости α.
3. Выбирается критерий – нормально распределенная случайная величина U.
4. Вычисляется выборочное значение критерия 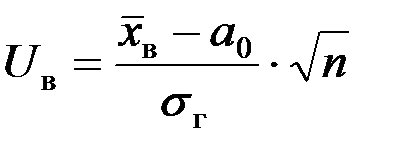 , где n – объем выборки.
, где n – объем выборки.
5. Выбирается критическая область по альтернативной гипотезе Н1, а критические точки uкр. по таблице значений функции Лапласа Ф(х), используя следующую схему
| Альтернативная гипотеза Н1 | |||||||||||
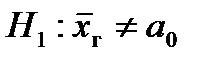 | 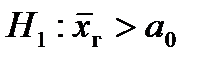 | 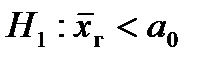 | |||||||||
| V1 – двусторонняя, симметричная. | V1 – правосторонняя | V1 – левосторонняя | |||||||||
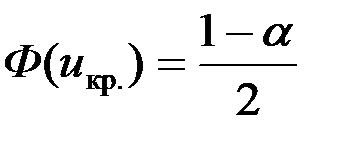 | 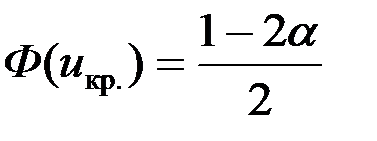 | 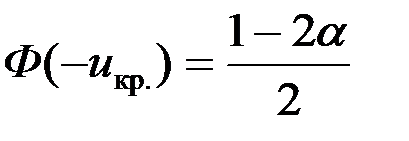 | |||||||||
6. Принимается статистическое решение.
Пример 9.1. Исследуется вопрос о соответствии нормативу по сборке пистолета Макарова результатов, показанных курсантами 3-го курса. Для этого было отобрано 144 человека, которым было предложено на время произвести сборку пистолета Макарова. Среднее время, затраченное на сборку для курсантов этой группы, оказалось равным 9,3 секунд. Исходя из опыта прошлых лет, средний разброс около норматива для всего 3-го курса можно считать равным 1,2 секунды. Норматив равен 9 секундам. При α = 0,01 оценить подготовленность курсантов, при предположении, что признак, характеризующий время, распределен по нормальному закону.
Решение. Примем норматив за возможное значение генеральной средней, т.е. а0 = 9. Из условия задачи ясно, что 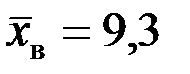 и
и 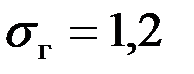 . Проведем проверку гипотезы по предложенной выше схеме.
. Проведем проверку гипотезы по предложенной выше схеме.
1. 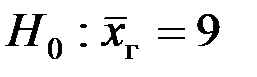 и
и 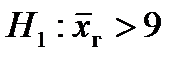 .
.
2. α = 0,01.
3. Критерий – нормально распределенная случайная величина U.
4. Выборочное значение критерия 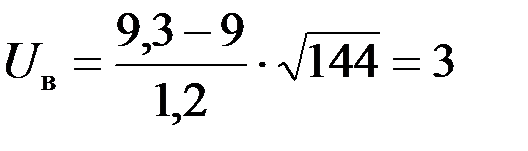 .
.
5. По альтернативной гипотезе 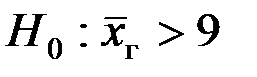 выбираем второй столбец схемы. Отсюда получаем, что V1 – правосторонняя критическая область.
выбираем второй столбец схемы. Отсюда получаем, что V1 – правосторонняя критическая область.
Критические точки uкр. определяем по таблице значений функции Лап ласа Ф(х) : 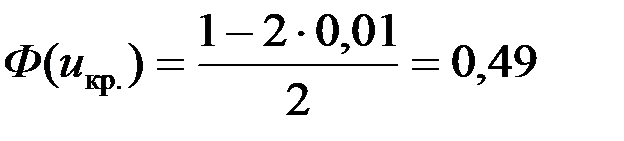 , следовательно, uкр. = 4,5. Строим критическую область и отмечаем на ней выборочное значение
, следовательно, uкр. = 4,5. Строим критическую область и отмечаем на ней выборочное значение
| икр.=4,5 |
| Uв=3 |
6. 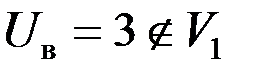 , следовательно, нет оснований отвергать основную гипотезу и считать, что курсанты 3 курса недостаточно хорошо проводят сборку пистолета Макарова. ■
, следовательно, нет оснований отвергать основную гипотезу и считать, что курсанты 3 курса недостаточно хорошо проводят сборку пистолета Макарова. ■
Рассмотрим еще одну задачу без текстового содержания.
Пример 9.2. Пусть из генеральной совокупности, признак которой распределен по нормальному закону, извлечена выборка объема n = 100. По значениям признака выборочных элементов найдена выборочная средняя 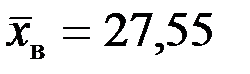 . Требуется при уровне значимости α = 0,05 проверить гипотезу о том, что генеральная средняя равна 28, если известно, что
. Требуется при уровне значимости α = 0,05 проверить гипотезу о том, что генеральная средняя равна 28, если известно, что 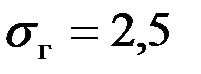 .
.
Решение.Проведем проверку этой гипотезы дважды, меняя альтернативную.
1. случай.
1. 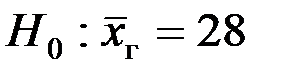 и
и 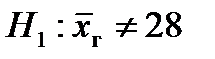 .
.
2. α = 0,05.
3. Критерий – нормально распределенная случайная величина U.
4. Выборочное значение критерия 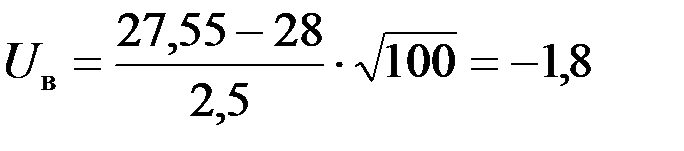 .
.
5. По альтернативной гипотезе 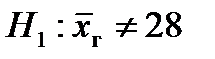 выбираем первый столбец схемы. Отсюда получаем, что V1 – двусторонняя симметричная критическая область. Критические точки uкр. определяем по таблице значений функции Лап ласа Ф(х) :
выбираем первый столбец схемы. Отсюда получаем, что V1 – двусторонняя симметричная критическая область. Критические точки uкр. определяем по таблице значений функции Лап ласа Ф(х) : 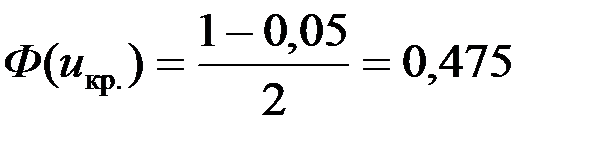 , следовательно, uкр. = 1,96. Строим критическую область и отмечаем на ней выборочное значение
, следовательно, uкр. = 1,96. Строим критическую область и отмечаем на ней выборочное значение
| икр.=1,96 |
| икр.=-1,96 |
| Uв=-1,8 |
6. 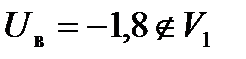 , следовательно, нет оснований отвергать основную гипотезу.
, следовательно, нет оснований отвергать основную гипотезу.
2 случай.
1. 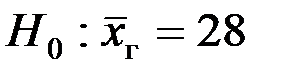 и
и 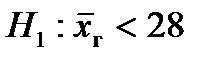 .
.
2. α = 0,05.
3. Критерий – нормально распределенная случайная величина U.
4. Выборочное значение критерия 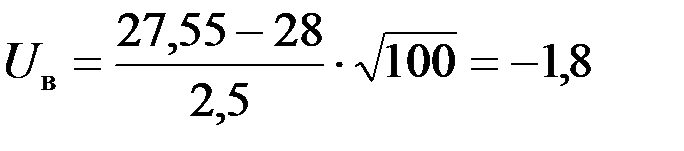 .
.
5. По альтернативной гипотезе 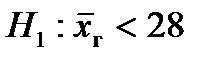 выбираем третий столбец схемы. Отсюда получаем, что V1 – левосторонняя критическая область.
выбираем третий столбец схемы. Отсюда получаем, что V1 – левосторонняя критическая область.
Критические точки uкр. определяем по таблице значений функции Лапласа Ф(х) : 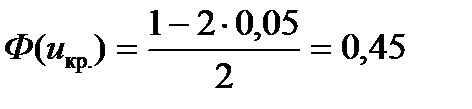 , следовательно, uкр. = -1,65. Строим критическую область и отмечаем на ней выборочное значение
, следовательно, uкр. = -1,65. Строим критическую область и отмечаем на ней выборочное значение
| икр.=-1,65 |
| Uв=-1,8 |
6. 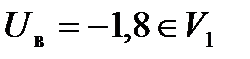 , следовательно, есть основания отвергнуть основную гипотезу. ■
, следовательно, есть основания отвергнуть основную гипотезу. ■
Рассмотрим второй вариант проверки гипотезы о генеральной средней.
I. 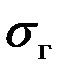 - неизвестно.
- неизвестно.
Как и в предыдущем случае, обратимся к общей схеме и конкретизируем каждый ее пункт для рассматриваемой гипотезы.
1. Формулируется основная гипотеза 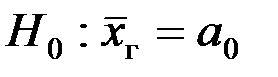 и одна из альтернативных
и одна из альтернативных 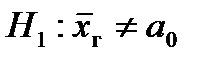 или
или 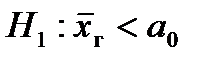 или
или 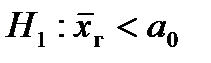 .
.
2. Выбирается уровень значимости α.
3. Выбирается критерий – случайная величина Т, распределенная по закону Стьюдента с числом степеней свободы ν = n – 1.
4. Вычисляется выборочное значение критерия 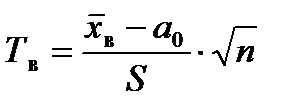 , где n – объем выборки, а S – исправленное среднее квадратическое отклонение.
, где n – объем выборки, а S – исправленное среднее квадратическое отклонение.
5. Выбирается критическая область по альтернативной гипотезе Н1, а критические точки tкр. по таблице критических точек распределения Стьюдента, используя следующую схему:
| Альтернативная гипотеза Н1 | |||||||||||
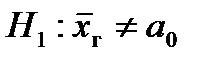 | 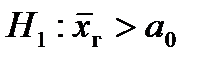 | 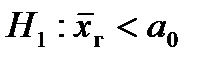 | |||||||||
| V1 – двусторонняя, симметричная. | V1 – правосторонняя | V1 – левосторонняя | |||||||||
| tкр. – в верхней строке, ν = n – 1. | tкр. – в нижней строке, ν = n – 1. | –tкр. – в нижней строке, ν = n – 1. | |||||||||
6. Принимается статистическое решение.
Рассмотрим задачи без текстового содержания.
Пример 9.3. Пусть из генеральной совокупности, признак которой распределен по нормальному закону, извлечена выборка объема n = 36. По значениям признака выборочных элементов найдены выборочная средняя 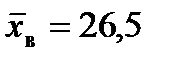 и выборочная дисперсия Dв = 8. Требуется при уровне значимости α = 0,01 проверить гипотезу о том, что генеральная средняя равна 26. В качестве альтернативной рассмотреть гипотезу о том, что генеральная средняя не равна 26.
и выборочная дисперсия Dв = 8. Требуется при уровне значимости α = 0,01 проверить гипотезу о том, что генеральная средняя равна 26. В качестве альтернативной рассмотреть гипотезу о том, что генеральная средняя не равна 26.
Решение. Проверку этой гипотезы проведем также по общей схеме.
1. 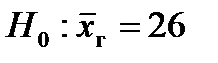 и
и 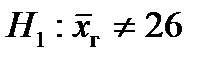 .
.
2. α = 0,01.
3. Критерий – случайная величина Т, распределенная по закону Стьюдента с числом степеней свободы ν = 36 – 1 = 35.
4. Для нахождения выборочного значения критерия найдем сначала величину 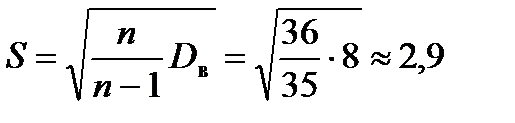 . Отсюда
. Отсюда 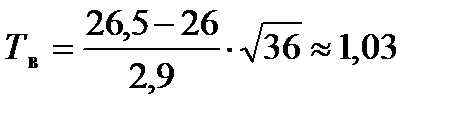 .
.
5. По альтернативной гипотезе 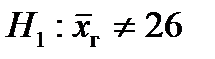 выбираем первый столбец схемы. Отсюда получаем, что V1 – двусторонняя симметричная критическая область.
выбираем первый столбец схемы. Отсюда получаем, что V1 – двусторонняя симметричная критическая область.
Критические точки tкр. определяем по таблице критических точек распределения Стьюдента: tкр.(0,01; 35) = 2,72. Строим критическую область и отмечаем на ней выборочное значение критерия
| 1,03 |
| tкр.=2,72 |
| tкр.=-2,72 |
6. 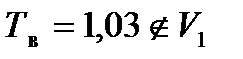 , следовательно, нет оснований для того, чтобы отвергнуть основную гипотезу. ■
, следовательно, нет оснований для того, чтобы отвергнуть основную гипотезу. ■
Пример 9.4. Из генеральной совокупности, признак которой распределен по нормальному закону, извлечена выборка и ее данные представлены в виде следующего статистического ряда:
| Значения признака хi | |||
| Частоты значений ni |
Требуется при уровне значимости α = 0,025 проверить гипотезу о том, что генеральная средняя равна 2,3.
Решение. Найдем вначале выборочную среднюю
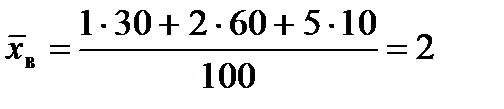 .
.
Нетрудно понять, что в этой ситуации в качестве альтернативной нужно взять гипотезу 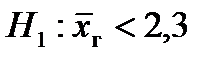 .
.
1. 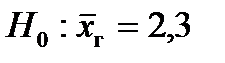 и
и 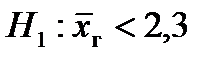 .
.
2. α = 0,025.
3. Критерий – случайная величина Т, распределенная по закону Стьюдента с числом степеней свободы ν = 100 – 1 = 99.
4. Для нахождения выборочного значения критерия найдем сначала величину 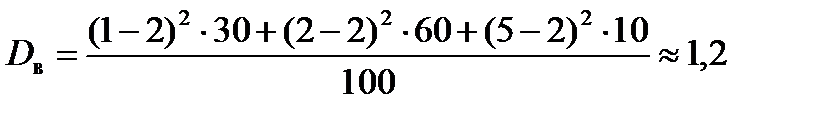 , а затем величину
, а затем величину 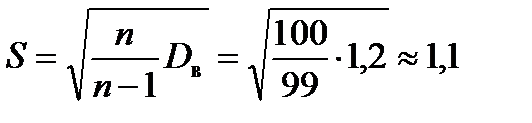 . Отсюда
. Отсюда 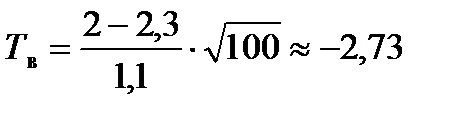 .
.
5. По альтернативной гипотезе 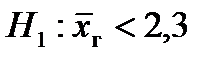 выбираем третий столбец схемы. Отсюда получаем, что V1 – левосторонняя критическая область.
выбираем третий столбец схемы. Отсюда получаем, что V1 – левосторонняя критическая область.
Критические точки tкр. определяем по таблице критических точек распределения Стьюдента : tкр.(0,025; 99) = -1,99. Строим критическую область и отмечаем на ней выборочное значение
| tкр.=-1,99 |
| Тв=-2,73 |
6. 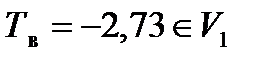 , следовательно, гипотеза Н0 отвергается, т.е. нельзя считать, что генеральная средняя равна 2,3. ■
, следовательно, гипотеза Н0 отвергается, т.е. нельзя считать, что генеральная средняя равна 2,3. ■
