ЕГОРКИНА Надежда Викторовна
А тобы
Өрнекті ықшамдаңыз:
А.01.
а)3a - (a - 1) + (2a - 5); б)6xy - x2 + 3 (x - y)2.
А.02.
а) 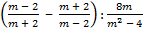 ; б)
; б) 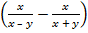 :
: 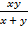 .
.
А.03.
а) 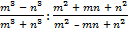 ; б)
; б) 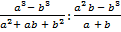 .
.
А.04.
а) 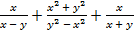 ; б)
; б) 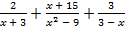 .
.
А.05.
а) 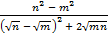 ; б)
; б) 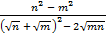 .
.
А.06.
а) 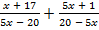 ; б)
; б) 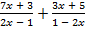 .
.
А.07.
а) 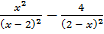 ; б)
; б) 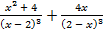 .
.
А.08.
а) 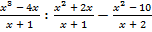 ; б)
; б) 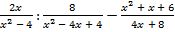 .
.
Көбейткіштерге жіктеңіз:
А.09.
а)у2 (2у – 5) – 8у + 20; б) 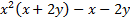 .
.
А.10.
а)4а2 + b – 2а – b2; б)a2 + 6a + 6b − b2.
А.11.
а)x2 – 7x + 7y – y2; б)a2 – 2bc + 2ac – ab.
А.12.
а)a3 – 5a2 – 4a + 20; б) 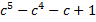 .
.
Бөлшекті қысқартыңыз:
А.13.
а) 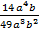 ; б)
; б) 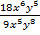 .
.
А.14.
а) 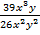 ; б)
; б) 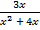 .
.
А.15.
а) 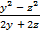 ; б)
; б) 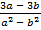 .
.
А.16.
а) 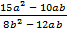 ; б)
; б) 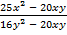 .
.
А.17.
а) 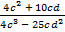 ; б)
; б) 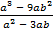 .
.
A.18.
а)  = 4 болғандағы
= 4 болғандағы 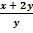 өрнегінің мәнін табыңыз.
өрнегінің мәнін табыңыз.
б)  = 3 болғандағы
= 3 болғандағы 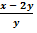 өрнегінің мәнін табыңыз.
өрнегінің мәнін табыңыз.
A.19.
а) 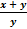 = 3 болғандағы
= 3 болғандағы  өрнегінің мәнін табыңыз.
өрнегінің мәнін табыңыз.
б) 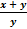 = 4 болғандағы
= 4 болғандағы 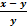 өрнегінің мәнін табыңыз.
өрнегінің мәнін табыңыз.
A.20.
а) Берілгена = 1, b = 3, c = 5, d = 3мәндерінде есептеңіз: 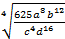 .
.
б) Берілгена=5, b=2, c=3, d=5мәндерінде есептеңіз: 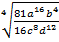 .
.
В тобы
В.21.
а) Түбірден шығарыңыз: 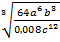 .
.
б) Түбірден шығарыңыз: 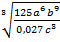 .
.
В.22.
а) Түбірден шығарып, берілген a= 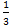 ; b=
; b= 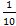 ; c=
; c=  мәндерінде есептеңіз:
мәндерінде есептеңіз: 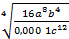 .
.
б) Түбірден шығарып, берілгенa = 3; b = 2; c = 1 мәндерінде есептеңіз: 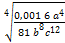 .
.
В.23.
а) Түбірден шығарыңыз: 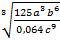 .
.
б) Түбірден шығарыңыз: 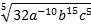 .
.
В.24.
а) Түбірден шығарып, берілгенa = 5; b = 1; c = 2 мәндерінде есептеңіз: 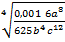 .
.
б) Түбірден шығарып, берілгена = 2, b = 3, c = 2 мәндерінде есептеңіз: 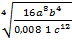 .
.
В.25.
а) Түбірден шығарыңыз: 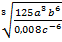 .
.
б) Түбірден шығарыңыз: 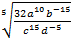 .
.
Өрнекті ықшамдаңыз:
В.26.
а)(0,2m2n3)3×1000m4n7; б)0,2a2b3(-5a3b)2.
В.27.
а)(ху)3(-3х4у2); б)-7с8 (-0,4с3)2.
В.28.
а) 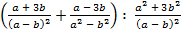 ;
;
б) 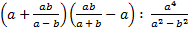 .
.
В.29.
а) 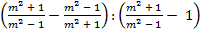 ;
;
б) 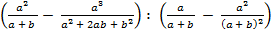 .
.
В.30.
а) 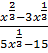 ; б)
; б) 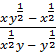 .
.
В.31.
а) 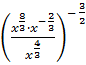 ; б)
; б) 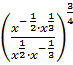 .
.
В.32.
а) 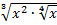 ; б)
; б) 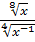 .
.
В.33.
а) 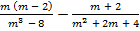 ; б)
; б) 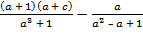 .
.
1 В.34. Бөліміндегі иррационалдықтан құтылыңыз:
а) 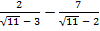 ; б)
; б) 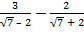 −
− 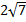 .
.
1 В.35. Өрнекті ықшамдап, оның мәнін табыңыз:
а) 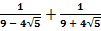 ; б)
; б) 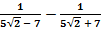 .
.
Өрнекті ықшамдаңыз:
В.36.
а) 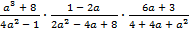 ;
;
б) 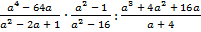 .
.
В.37.
а) 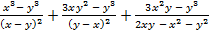 ;
;
б) 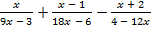 .
.
В.38.
а) 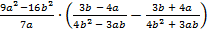 ;
;
б) 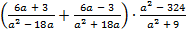 .
.
В.39.
а) 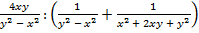 ;
;
б) 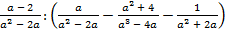 .
.
В.40.
а) 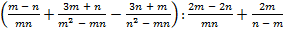 ;
;
б) 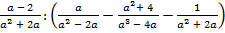 .
.
В.41.
а) 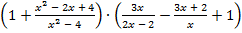 ;
;
б) 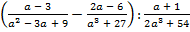 .
.
B.42.
а) 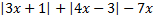 , егер
, егер 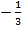
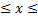
 ;
;
б) 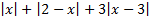 , егер 0 < x < 2.
, егер 0 < x < 2.
1 B.43. Функцияның ең кіші мәнін табыңыз:
а) 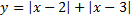 ;
;
б) 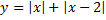 .
.
B.44.
а) Ықшамдаңыз 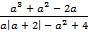 . Мұнда
. Мұнда 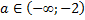 .
.
б) Бөлшекті қысқартыңыз: 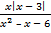 .
.
С тобы
1 C.45. Өрнекті ықшамдаңыз:
а) 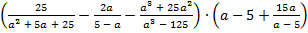 ;
;
б) 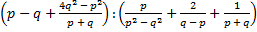 .
.
1 С.46. Көбейткіштерге жіктеңіз:
а) 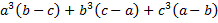 ;
;
б) 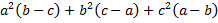 .
.
1 С. 47. Өрнекті ықшамдаңыз:
а) 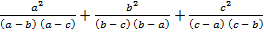 ;
;
б) 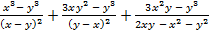 .
.
1 С.48. Өрнекті ықшамдаңыз:
а) 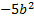
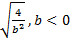 ; б)
; б) 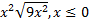 .
.
1 С.49. Өрнекті ықшамдаңыз:
а) 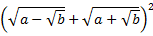 ; б)
; б) 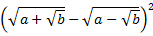 .
.
1 С.50. Бөліміндегі иррационалдықтан құтылыңыз:
а) 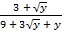 ; б)
; б) 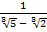 .
.
1 С.51. Бөліміндегі иррационалдықтан құтылыңыз:
а) 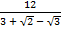 ; б)
; б) 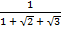 .
.
1 С.52. Бөліміндегі иррационалдықтан құтылыңыз:
а) 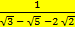 ; б)
; б) 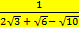 .
.
1 С.53. Бөліміндегі иррационалдықтан құтылыңыз:
а) 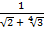 ; б)
; б) 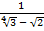 .
.
Өрнекті ықшамдаңыз:
С.54.
а) 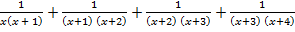 ;
;
б) 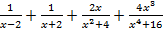 .
.
С.55.
а) 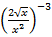
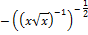 ;
;
б) 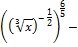
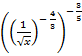 .
.
2-бөлім. Алгебралық теңдеулер және теңдеулер жүйелері
А тобы
2 А.01. Пропорцияның белгісіз мүшесін табыңыз:
а) 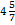 x :
x : 
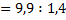 ; б)1
; б)1  : х = 2
: х = 2  :
: 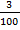 .
.
А.02.
а) 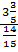 =
= 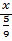 ; б)
; б) 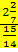 =
=  .
.
Теңдеуді шешіңіз:
А.03.
а) 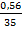 =
= 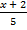 ; б)
; б) 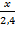 =
= 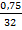 .
.
А.04.
а) 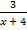 =
= 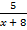 ; б)
; б) 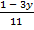 −
− 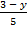 = 0.
= 0.
А.05.
а)6 = 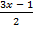 · 2,4; б)0,69 =
· 2,4; б)0,69 = 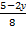 · 13,8.
· 13,8.
А.06.
а)- (7у + 0,6) = 3,6 - у; б)6 (х - 1) = 9,4 - 1,7х.
А.07.
а)5 - 3 (х - 2 (х - 2 (х - 2))) = 2;
б)10 (1,37у - 0,12у) : 5 : 8 = 0.
А.08.
а)2х - 3 + 2 (х - 1) = 4 (х - 1) - 7;
б)2х + 3 - 6 (х - 1) = 4 (1 - х) + 5.
А.09.
а)4х2 + 5х = 9х2 - 15х; б)х2 - 7х + 6 = 0.
А.10.
а)х2 + 2х + 1 = 0; б)х2 + 12х - 64=0.
А.11.
а)2х2 - 7х + 5 = 0; б)х2 + 14х + 24 = 0.
А.12.
а)4х2 + 12х + 9 = 0; б)10х2 - х + 1 = 0.
А.13.
а) 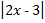 = 1; б)
= 1; б) 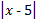 = 3.
= 3.
А.14.
а) 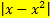 = 6; б)
= 6; б) 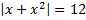 .
.
А.15.
а)ï2х + 1ï = х; б) 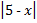 = 2 (2х - 5).
= 2 (2х - 5).
А.16.
а) 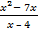 =
= 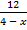 ; б)
; б) 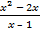 =
= 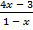 .
.
А.17.
а) 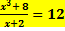 ; б)
; б) 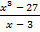 = 27.
= 27.
А.18.
а) 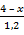 =
= 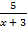 ; б)
; б) 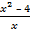 =
= 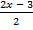 .
.
А.19.
а) а-ның(а ¹ 0) қандай мәндерінде ах2-4х + 2 квадрат үшмүшеліктің әр түрлі екі түбірі болады?
б) c-ның қандай мәнінде 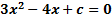 теңдеуінің бірдей екі түбірі болады?
теңдеуінің бірдей екі түбірі болады?
Теңдеулер жүйесін шешіңіз:
А.20.
а) 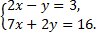 б)
б) 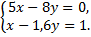
А.21.
а) 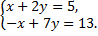 б)
б) 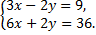
А.22.
а) 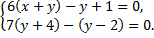
б) Егер 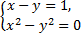 х + у мәні неге тең?
х + у мәні неге тең?
B тобы
Теңдеуді шешіңіз:
B.23.
а) 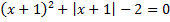 ; б)
; б) 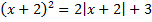 .
.
B.24.
а) 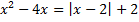 ; б)
; б) 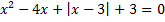 .
.
B.25.
а) 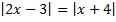 ; б)
; б) 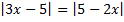 .
.
B.26.
а) 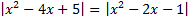 ;
;
б) 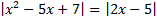 .
.
B.27.
а) 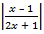 =
= 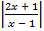 ; б)
; б) 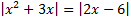 .
.
B.28.
а) 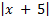 -
- 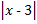 = 8; б)
= 8; б) 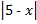 +
+ 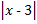 = 2.
= 2.
B.29.
а) 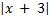 +
+ 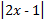 = 8; б)ï5 - 2хï + ïх + 3ï = 2 - 3х.
= 8; б)ï5 - 2хï + ïх + 3ï = 2 - 3х.
B.30.
а) 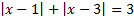 ;
;
б) 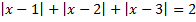 .
.
B.31.
а) 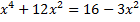 ; б)
; б) 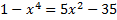 .
.
B.32.
а) 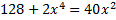 ; б)
; б) 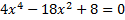 .
.
B.33.
а) 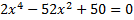 ; б)
; б) 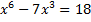 .
.
B.34.
а) Теңдеудің түбірлерінің квадраттарының қосындысын табыңыз: х2 + 3х - 15 = 0.
б) Теңдеудің түбірлерінің кубтарының қосындысын табыңыз: х2 + 3х - 15 = 0.
B.35.
а) Егер 1,732< 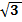 < 1,734 болса, 0,99 санына ең жақын болатын теңдеудің түбірін табыңыз:
< 1,734 болса, 0,99 санына ең жақын болатын теңдеудің түбірін табыңыз:
(x2- 2x - 2) (x2 - 2x - 3)=0.
б) Егер 1,732< 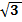 < 1,734 болса, онда
< 1,734 болса, онда
(х2- 7х + 8) (2х2 + 2х - 1) = 0 теңдеуінің неше түбірі
(-1,366; 0,365) аралығында жатады?
B.36.
а) Есептеңіз: 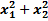 . Бұнда х1, х2 – келесі теңдеудің түбірлері: х2-
. Бұнда х1, х2 – келесі теңдеудің түбірлері: х2- 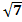 х + 1 =
х + 1 = 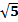 х + 2.
х + 2.
б) Есептеңіз: 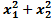 . Бұнда х1, х2 – келесі теңдеудің түбірлері:
. Бұнда х1, х2 – келесі теңдеудің түбірлері:
х2 - 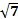 х + 1 = -
х + 1 = - 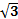 х + 2.
х + 2.
B.37.
а) Есептеңіз: 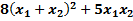 . Бұнда
. Бұнда 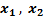 – келесі теңдеудің түбірлері:
– келесі теңдеудің түбірлері: 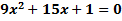 .
.
б) 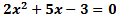 теңдеуінің
теңдеуінің 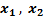 түбірлерін таппай, келесі өрнектің мәнін есептеңіз:
түбірлерін таппай, келесі өрнектің мәнін есептеңіз: 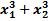 .
.
B.38.
а) Егер 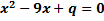 теңдеуінің түбірлері
теңдеуінің түбірлері 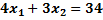 шартын қанағаттандырса, q-дің мәні неге тең?
шартын қанағаттандырса, q-дің мәні неге тең?
б) 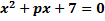 теңдеуінің
теңдеуінің 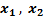 түбірлері оң және
түбірлері оң және 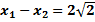 . р-нің мәнін табыңыз.
. р-нің мәнін табыңыз.
B.39.
а) Түбірлері 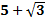 және
және 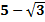 болатын квадрат теңдеуді жазыңыз.
болатын квадрат теңдеуді жазыңыз.
B.40.
а) х-тің алдындағы коэффициенті (–1)-ге тең және бір түбірі екіншісінен 3-ке артық болатын келтірілген квадрат теңдеуді жазыңыз.
б) х-тің алдындағы коэффициенті (–5)-ге тең және бір түбірі екіншісінен 1-ге артық болатын келтірілген квадрат теңдеуді жазыңыз.
Теңдеуді шешіңіз:
B.41.
а) 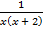 +
+ 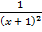 =
= 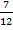 ; б)
; б) 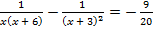 .
.
B.42.
а) 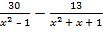 =
= 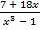 ; б)
; б) 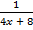 =
= 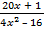 −
− 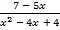 .
.
B.43.
а) 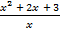 –
– 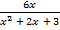 = 5; б)
= 5; б) 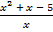 +
+ 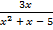 + 4 = 0.
+ 4 = 0.
B.44.
а) 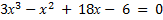 ; б)х3 + х2 = 9х + 9.
; б)х3 + х2 = 9х + 9.
B.45.
а)2х3 + 8х = х2 + 4; б) 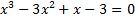 .
.
B.46.
а) 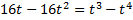 ; б)
; б) 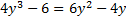 .
.
Теңдеулер жүйесін шешіңіз:
B.47.
а) 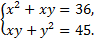 б)
б) 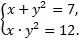
B.48.
а) 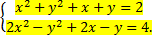 б)
б) 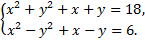
B.49.
а) 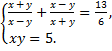 б)
б) 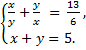
B.50.
а) 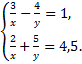 б)
б) 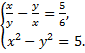
B.51.
а) 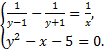 б)
б) 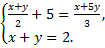
B.52.
а) 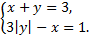 б)
б) 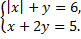
B.53.
а) 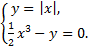 б)
б) 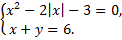
B.54.
а) 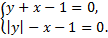 б)
б) 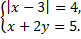
B.55.
а) 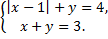 б)
б) 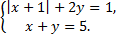
B.56.
а) 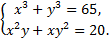 б)
б) 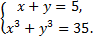
B.57.
а) 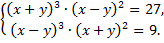 б)
б) 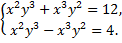
B.58.
а) Есептеңіз: (3х+2)(2у+1)(3у+1)(2х+2).Бұнда х, у – келесі теңдеулер жүйесінің шешімдері: 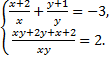
б) Есептеңіз: (3х+1)(2у+1)+(3у+1)(2х+1). Бұнда х, у – келесі теңдеулер жүйесінің шешімдері: 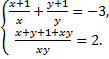
B.59.
а) Есептеңіз: (3х+1)(3у-1)+(2у-1)(2х+1). Бұнда х, у – келесі теңдеулер жүйесінің шешімдері: 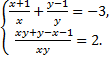
б) Есептеңіз: 12ху+6(х+у). Бұнда х, у – келесі теңдеулер жүйесінің шешімдері:
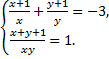
C тобы
Теңдеуді шешіңіз:
C.60.
а) 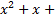
 +
+ 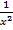 = 4; б)
= 4; б) 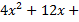
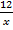 +
+ 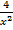 = 47.
= 47.
C.61.
а) 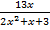 +
+ 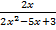 = 6; б)
= 6; б) 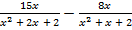 = 1.
= 1.
C.62.
а) 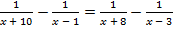 ; б)
; б) 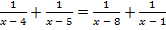 .
.
C.63.
а) 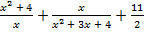
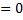 ; б)
; б) 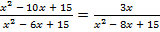 .
.
C.64.
а) Параметра–ның барлық мәндерінде теңдеуді шешіңіз: 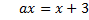 .
.
б) Параметр а–ның барлық мәндерінде теңдеуді шешіңіз: 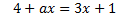 .
.
Теңдеулер жүйесін шешіңіз:
C.65.
а) 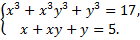 б)
б) 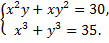
C.66.
а) 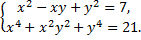
б) 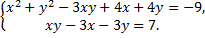
C.67.
а) а-ның қандай мәндерінде 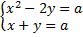 теңдеулер жүйесінің жалғыз шешімі болады?
теңдеулер жүйесінің жалғыз шешімі болады?
б) а-ның қандай мәндерінде 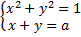 теңдеулер жүйесінің жалғыз шешімі болады?
теңдеулер жүйесінің жалғыз шешімі болады?
C.68.
а) а-ның қандай мәндерінде 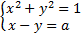 теңдеулер жүйесінің жалғыз шешімі болады?
теңдеулер жүйесінің жалғыз шешімі болады?
б) а-ның қандай мәндерінде 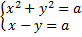 теңдеулер жүйесінің жалғыз шешімі болады?
теңдеулер жүйесінің жалғыз шешімі болады?
C.69.
а) 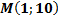 және
және 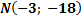 нүктелері арқылы өтетін
нүктелері арқылы өтетін 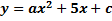 парабола теңдеуінің а және с коэффициенттерін табыңыз.
парабола теңдеуінің а және с коэффициенттерін табыңыз.
б) 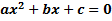 теңдеуінің бір ғана шешімі
теңдеуінің бір ғана шешімі 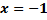 . Қосындылары 1-ге тең болатын a, b, с сандарын табыңыз.
. Қосындылары 1-ге тең болатын a, b, с сандарын табыңыз.
C.70.
а) k-ның қандай мәндерінде 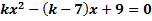 теңдеуінің түбірілері бірдей және теріс мәнді болады?
теңдеуінің түбірілері бірдей және теріс мәнді болады?
б) а-ның қандай мәндерінде 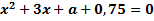 теңдеуінің екі түбірі де теріс мәнді болады?
теңдеуінің екі түбірі де теріс мәнді болады?
3-бөлім. Алгебралық теңсіздіктер және
теңсіздіктер жүйелері
А тобы
А.01.
а) х -тың қандай мәндерінде келесі теңсіздік орындалады:
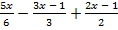 < 1?
< 1?
б) Теңсіздіктің ең үлкен бүтін шешімін табыңыз:
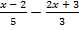 > 1.
> 1.
Теңсіздікті шешіңіз:
А.02.
а) 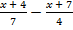 > −3; б)
> −3; б) 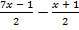 > x.
> x.
А.03.
а) 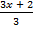 − x − 1 >
− x − 1 > 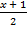 ; б)
; б) 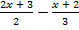 >
> 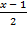 .
.
А.04.
а) 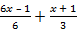 >
> 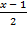 ; б)
; б) 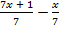 >
> 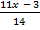 .
.
А.05.
а) 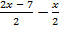 > x + 1; б)x + 2
> x + 1; б)x + 2 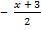 >
>  .
.
А.06.
а) 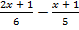 >
> 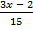 ; б)
; б) 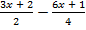 >
> 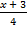 .
.
А.07.
а)–3x > –9; б)–2x > 4.
А.08.
а)–3x ³  ; б)
; б) 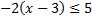 .
.
А.09.
а) 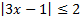 ; б)
; б) 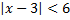 .
.
А.10.
а) 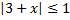 ; б)
; б) 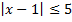 .
.
А.11.
а) 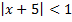 ; б)
; б) 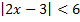 .
.
А.12.
а) 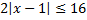 ; б)
; б) 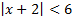 .
.
А.13.
а) 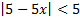 ; б)
; б) 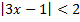 .
.
А.14.
а) 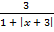 < 1; б)
< 1; б) 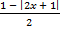 > −3.
> −3.
А.15.
а) 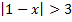 ; б)
; б) 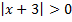 .
.
А.16.
а) 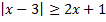 ; б)
; б) 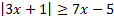 .
.
Теңсіздіктер жүйесін шешіңіз:
А.17.
а) 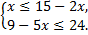 б)
б) 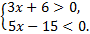
А.18.
а) 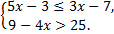 б)
б) 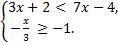
А.19.
а) 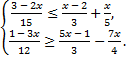 б)
б) 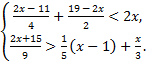
А.20.
а) 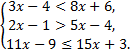 б)
б) 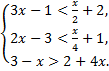
Теңсіздікті шешіңіз:
А.21.
а) 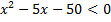 ; б)
; б) 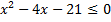 .
.
А.22.
а) 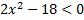 ; б)
; б) 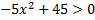 .
.
А.23.
а) 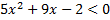 ; б)
; б) 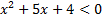 .
.
А.24.
а) 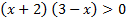 ; б)
; б) 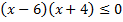 .
.
А.25.
а) 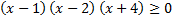 ;
;
б) 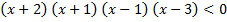 .
.
А.26.
а) 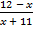 > 0; б)
> 0; б) 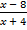 < 0.
< 0.
А.27.
а) 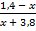 > 0; б)
> 0; б) 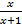 ≥ 0.
≥ 0.
А.28.
а) 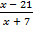 < 0; б)
< 0; б) 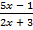 ≥ 0.
≥ 0.
А.29.
а) 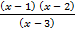 ≥ 0; б)
≥ 0; б) 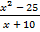 ≥ 0.
≥ 0.
А.30.
а) 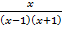 ≤ 0; б)
≤ 0; б) 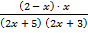 ≥ 0.
≥ 0.
А.31.
а) 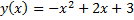 функциясы берілген.
функциясы берілген. 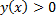 теңсіздігін шешіңіз.
теңсіздігін шешіңіз.
б) 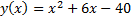 функциясы берілген.
функциясы берілген. 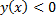 теңсіздігін шешіңіз.
теңсіздігін шешіңіз.
B тобы
B.32.
а) Теңсіздіктің ең үлкен бүтін шешімін табыңыз:
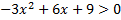 .
.
б) Теңсіздіктің ең кіші бүтін шешімін табыңыз:
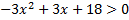 .
.
Теңсіздікті шешіңіз:
B.33.
а) 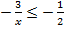 ; б)
; б) 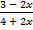 > 1.
> 1.
B.34.
а) 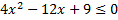 ; б)
; б) 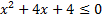 .
.
B.35.
а) 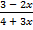 > 1; б)
> 1; б) 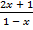 < −3.
< −3.
B.36.
а) 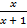 ≤ 2; б)
≤ 2; б) 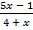 < −2.
< −2.
B.37.
а)–х2 + 3х – 4 > 0; б)3x - x2 - 4 < 0.
B.38.
а) 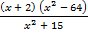 ≤ 0; б)
≤ 0; б) 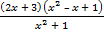 < 0.
< 0.
B.39.
а) 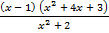 ≥ 0; б)
≥ 0; б) 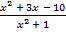 ≤ 0.
≤ 0.
B.40.
а) 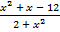 < 0; б)
< 0; б) 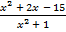 < 0.
< 0.
B.41.
а) 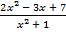 > 3; б)
> 3; б) 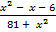 < 0.
< 0.
B.42.
а) 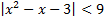 ; б)
; б) 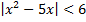 .
.
B.43.
а) 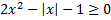 ; б)
; б) 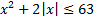 .
.
B.44.
а) 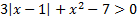 ; б)
; б) 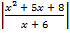 + x > 3.
+ x > 3.
B.45.
а) 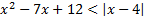 ; б)
; б) 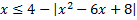 .
.
Теңсіздіктер жүйесін шешіңіз:
B.46.
а) 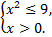 б)
б) 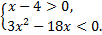
B.47.
а) 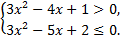 б)
б) 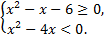
B.48.
а) 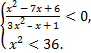 б)
б) 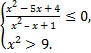
B.49.
а) 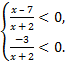 б)
б) 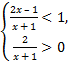
B.50.
а) 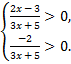 б)
б) 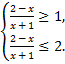
С тобы
C.51.
а) 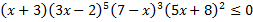 ;
;
б) 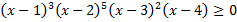 .
.
C.52.
а) 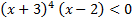 ;
;
б) 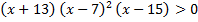 .
.
C
