Орієнтовний перелік питань для підсумкового контролю знань
ЗМІСТ
ВСТУП ............................................................................................................ 4
ОСНОВНІ ПИТАННЯ ПРОГРАМИ ДИСЦИПЛІНИ ЗА ТЕМОЮ
«ЛІНІЙНА ТА ВЕКТОРНА АЛГЕБРА» ....................................................... 5
ОРІЄНТОВНИЙ ПЕРЕЛІК ПИТАНЬ ДЛЯ ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ 6
1. ЛІНІЙНА АЛГЕБРА .................................................................................. 7
1.1. Матриці та дії над ними .......................................................................... 7
1.2. Визначення та основні властивості визначників .................................. 11
1.3. Системи лінійних алгебраїчних рівнянь .............................................. 14
2. ВЕКТОРНА АЛГЕБРА ............................................................................ 20
2.1. Поняття вектора та лінійні операції над векторами ............................ 20
2.2. Вектори у декартовій системі координат ............................................. 22
2.3. Скалярний, векторний та мішаний добутки векторів .......................... 23
МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ВИКОНАННЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ 25
СПИСОК ЛІТЕРАТУРИ .............................................................................. 27
Додаток А
ІНДИВІДУАЛЬНІ ЗАВДАННЯ ЗА ТЕМОЮ «ЛІНІЙНА ТА ВЕКТОРНА АЛГЕБРА» ................................................................................................................... ….28
Вступ
Методичні вказівки відповідають програмі курсу «Вища математика» для студентів технологічних спеціальностей та можуть бути використані при виконанні індивідуальних завдань за темою «Лінійна та векторна алгебра».
Особливістю посібника є наявність завдань для тетраместрових індивідуальних робіт у кількості, достатній для академічних груп.
Дані методичні вказівки є довідковим матеріалом. Вони містять визначення, формули, деякі теоретичні відомості. Мета роботи – надати в невеликому за обсягом довіднику деякі відомості з вищої математики, необхідні при вивченні тем: «Матриці», «Визначники», «Системи лінійних рівнянь», «Векторна алгебра».
Слід мати на увазі, що це – не навчальна книга, не конспект лекцій, а короткий довідковий матеріал, який не може замінити вивчення лекційного матеріалу та навчальної літератури.
Кожен розділ посібника, охоплюючи ту чи іншу тему, містить необхідні теоретичні положення.
Перед розв’язуванням задач необхідно вивчити відповідні розділи теоретичного матеріалу.
Основні питання Програми дисципліни за темою «Лінійна та векторна алгебра»
| 1. Матриці. Дії над матрицями: | |
| Поняття прямокутноїматриці. Види матриць. Дії з матрицями та їх властивості. Поняття рангу матриці. Методи знаходження рангу. Теореми про ранг матриці. | |
| 2. Визначники. Властивості визначників і способи їх обчислення: | |
| Поняття визначника. Мінор та алгебраїчне доповнення. Властивості та методи обчислення визначників другого та третього порядків. Визначники n-го порядку, їх властивості та обчислення. | |
| 3. Системи лінійних алгебраїчних рівнянь (СЛАР): | |
| Основні поняття та визначення. Правило Крамера для розв’язування СЛАР. Матрична форма запису СЛАР. Поняття та знаходження оберненої матриці. Розв’язування СЛАР за допомогою оберненої матриці. Умови існування та одиничності розв’язку. Однорідні СЛАР, умови одиничності розв’язку. | |
| 4. Поняття вектора та скаляра. Основні характеристики та визначення. Лінійні операції над векторами: | |
| Поняття скаляра та вектора. Види векторів. Рівність векторів. Лінійні операції над векторами: додавання, віднімання та множення на скаляр. Одиничний вектор. Колінеарність та компланарність векторів. Лінійна залежність, незалежність векторів. Проекція вектора на вісь, її властивості. | |
| 5. Скалярний добуток векторів: | |
| Визначення, основні властивості, геометричний зміст. Скалярний добуток векторів у координатній формі запису. Застосування скалярного добутку (довжина вектора, кут між векторами, проекція одного вектора на напрямок іншого, умова перпендикулярності векторів). | |
| 6. Векторний добуток векторів: | |
| Визначення, основні властивості, геометричний зміст. Векторний добуток векторів у координатній формі запису. Застосування векторного добутку (площа, висота паралелограма та трикутника, умова колінеарності двох векторів). | |
| 7. Мішаний добуток векторів: | |
| Визначення, основні властивості, геометричний зміст. Мішаний добуток векторів у координатній формі запису. Застосування мішаного добутку (об’єм, висота паралелепіпеда та піраміди, умова компланарності векторів). |
ОРІЄНТОВНИЙ ПЕРЕЛІК ПИТАНЬ ДЛЯ ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ
1. Прямокутні, квадратні матриці (основні визначення). Дії над матрицями.
2. Визначники. Мінори. Алгебраїчні доповнення.
3. Властивості визначників.
4. Визначники 2-го та 3-го порядку, способи їх обчислення.
5. Ранг матриці. Теорема Кронекера-Капеллі.
6. Обернена матриця. Теорема про існування оберненої матриці.
7. Теорема Крамера. Формули Крамера.
8. Матричний метод розв’язування систем лінійних алгебраїчних рівнянь.
9. Метод Гаусса розв’язування систем лінійних алгебраїчних рівнянь.
10. Однорідні системи лінійних алгебраїчних рівнянь. Умова існування нетривіального рішення однорідної системи.
11. Визначення вектора. Координата вектора. Довжина та напрямок вектора.
12. Скалярні та векторні величини. Лінійні дії з векторами.
13. Вектор у просторовій декартовій системі координат. Дії над векторами, які задані своїми координатами.
14. Скалярний добуток векторів, його властивості та застосування.
15. Векторний добуток векторів, його властивості та застосування.
16. Мішаний добуток векторів, його властивості та застосування.
Лінійна алгебра
Матриці та дії над ними
Матрицею розміру 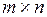 називається множина з елементів
називається множина з елементів 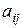 , розміщених у вигляді прямокутної таблиці з
, розміщених у вигляді прямокутної таблиці з 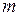 рядків і
рядків і 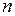 стовпців:
стовпців:
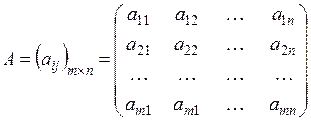 ,
,
де 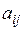 – елемент матриці; числа
– елемент матриці; числа 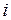 ,
, 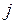 – індекси елемента матриці, що вказують його місцезнаходження:
– індекси елемента матриці, що вказують його місцезнаходження: 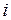 – номер рядка;
– номер рядка; 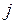 – номер стовпця.
– номер стовпця.
Число елементів матриці 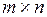 знаходиться як добуток числа рядків
знаходиться як добуток числа рядків 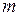 на число стовпців
на число стовпців 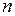 .
.
Матриця називається прямокутною, якщо число її рядків не дорівнює числу її стовпців, тобто 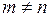 :
:
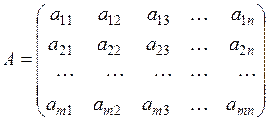 .
.
Квадратною матрицею називається матриця, в якій кількість рядків і стовпців однакова. Їх кількість вказує на розмір (порядок) матриці:
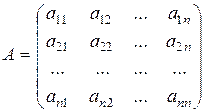 .
.
Головною діагоналлю квадратної матриці називається діагональ, яка проходить через лівий верхній та правий нижній кути матриці (складається із елементів 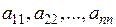 ): ):  | Побічною діагоналлю квадратної матриці називається діагональ, яка проходить через правий верхній та лівий нижній кути матриці (складається із елементів 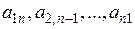 ): ): 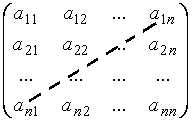 |
Деякі типи матриць
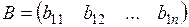 | Матриця-рядок – матриця розмірності 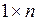 , яка містить всього один рядок , яка містить всього один рядок |
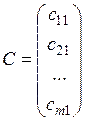 | Матриця-стовпець – матриця розмірності 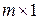 , яка містить всього один стовпець , яка містить всього один стовпець |
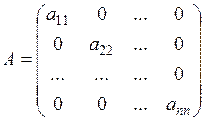 | Діагональна матриця –квадратна матриця, в якій всі елементи, що знаходяться поза головною діагоналлю, дорівнюють нулю |
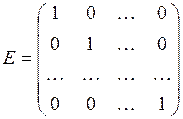 | Одинична матриця – діагональна матриця, в якій всі елементи, що містяться на головній діагоналі, дорівнюють одиниці (позначають літерою Е) |
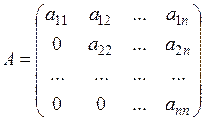 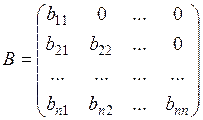 | Трикутна матриця –матриця, всі елементи якої під (над) головною діагоналлю дорівнюють нулю |
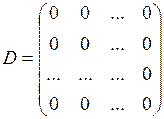 | Нульова матриця – матриця, всі елементи якої дорівнюють нулю |
Дії над матрицями
| 1. Операція порівняння: | |
| Дві матриці нази-ваються рівними, якщо рівні їх відповідні елементи | Якщо 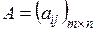 та та 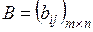 , то , то 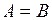 , коли , коли 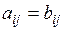 ( ( 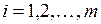 ; ; 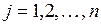 ) ) |
| 2. Множення матриці на число: | |
| Щоб помножити матрицю на дійсне число відмінне від нуля, необхідно кожен елемент матриці помножити на це число | Якщо 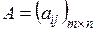 та та 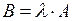 , то , то 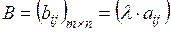 : : 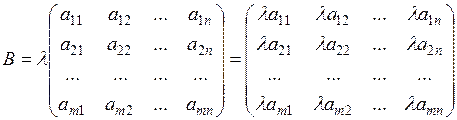 |
| 3. Додавання (віднімання) матриць: | |
| Щоб знайти суму (різницю) двох матриць (однако-вого розміру), необхідно скласти (відняти) елементи з однаковими індек-сами (що розташо-вані на однакових місцях) Зауваження. Додавати (віднімати) можна лише матриці з однаковою кіль-кістю рядків і стовпців | Якщо 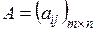 , , 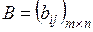 та та 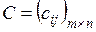 , то , то 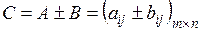 : : 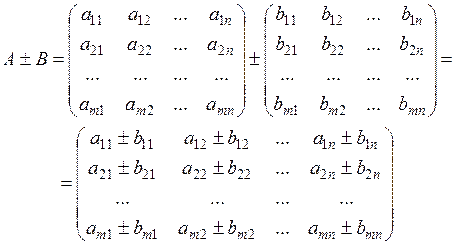 Властивості операції додавання (віднімання) матриць: Властивості операції додавання (віднімання) матриць: 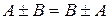 (комутативність); (комутативність); 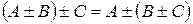 (асоціативність); (асоціативність); 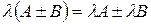 (дистрибутивність); (дистрибутивність); 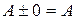 (нейтральність нульової матриці) (нейтральність нульової матриці) |
Продовження
