Оценка параметров уравнения регрессии по МНК

Для оценки параметров функции используется метод наименьших квадратов.

МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений признака y от теоретических минимальна:

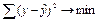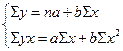Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно и :

Условия применения МНК:

· модель регрессии должна быть линейной по параметрам

· х – не стохастическая переменная (заданная величина)

· значения ошибки – случайные. Их изменение не образует определенной модели

· число наблюдений должно быть больше числа оцениваемых параметров (5-6 раз)

· значения переменной x не должны быть одинаковыми

· изучаемая совокупность должна быть достаточно однородной

· отсутствие взаимосвязи между фактором x и остатком

· модель регрессии должна быть корректно специфицирована

· в модели не должно наблюдаться тесной взаимосвязи между факторами

Доказательство.

На основании необходимого условия существования экстремума функции 2-х переменных S(а,в) - находим её частные производные и приравнивая их к нулю:

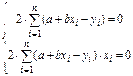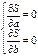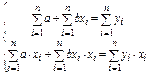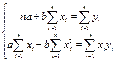(1.5)

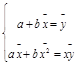Систему (1.5) называется системой нормальных уравнений. Разделив обе части уравнений (1.5) на n и получим систему нормальных уравнений в виде:

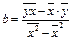Отсюда получаем оценки

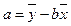a- свободный член уравнения регрессии. Экономически не интерпретируется.

b -наклон линии регрессии или коэффициент регрессии. Он является мерой зависимости переменной от переменной. В линейном уравнении регрессии параметр является абсолютным показателем силы связи.

Понятие корреляции.

Корреляция —это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой Корреляции двух случайных величин служит коэффициент Корреляции.

Ур-е регрессии всегда дополняется показателем тесноты связи. При использовании лин. регрессии, в качестве такого показателя выступает линейный коэффициент корреляции r_xy.

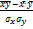r_xy = , где σ_x, σ_y – С.К.О.

В случае, если:

r_xy > 0 – связь прямая;

r_xy < 0 – связь обратная;

r_xy = 0 – связь отсутствует.

r_xy = b 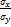, но учитывая

b = 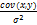, то получаем:

r = .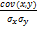

Свойства выборочного коэф-та корреляции:

· Значения коэф-та корреляции лежат в промежутке -1 £ r £ 1;

· Чем ближе |r_xy| к 1, тем теснее связь между Х и У.

· Все точки лежат на прямой, следовательно, функциональная связь.

r_xy = 1; r_xy = -1; r_xy = 0.

В некоторых случаях, например, когда зависимость между х и у не является линейной, коэф-т r_xy нельзя рассматривать как строгую меру связи между х и у.

Регрессия:	Корреляция:
Позволяет изучить форму связи;	Позволяет изучить тесноту связи;
Выраж. моделью (уравн-ем);	Выраж. числом (коэф-ом rxy );
Использует различн. виды ур-ий (линейн, параболы, др.)	-1 £ rxy £ 1 .