Работа по перемещению проводника с током в магнитном поле

В настоящем параграфе на простой модели будет получено полезное соотношение для расчета работы при движении проводника с током в магнитном поле.

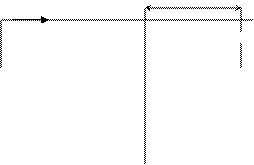
Пусть имеется цепь, по которой течет постоянный ток. Провод длиной L, изображенный на рисунке вертикальным, может скользить по горизонтальным подводящим проводам, сохраняя электрический контакт с ними. Вся схема находится во внешнем однородном магнитном поле, перпендикулярном плоскости рисунка. При этом на подвижный проводник будет действовать сила Ампера, также изображенная на рисунке.

Вычислим работу силы Ампера при перемещении проводника равным .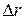

I

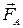
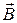L

Рис.8.1

Вычисление работы представим последовательностью формул:

,

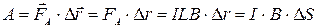где .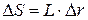

Здесь учтено, во-первых, сила перпендикулярна перемещению; во-вторых, ток в проводнике перпендикулярен магнитному полю. Кроме того, введено обозначение 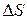для площади, покрытой проводником при движении. Эта величина представляет собой увеличение площади замкнутого контура, по которому течет ток.

Величина 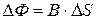представляет собой поток вектора магнитной индукции (или магнитный поток) через площадку 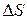, перпендикулярную магнитному полю. В случае произвольной площадки поток вектора магнитной индукции 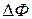равен:

,

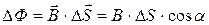где a - угол между направлением вектора 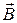и нормалью к площадке.

Нетрудно заметить, что понятие магнитного потока аналогично потоку вектора напряженности электрического поля. В физике рассматриваются потоки и других векторных полей, причем все они определяются аналогично. Например, поток вектора скорости несжимаемой жидкости через площадь поперечного сечения трубы равен объему жидкости, протекающей через сечение трубы за единицу времени.

Таким образом, полученная нами формула для работы может быть записана с использованием понятия магнитного потока:

,

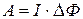что означает, что работа по перемещению проводника с постоянным током в магнитном поле равна величине тока умноженной на изменение магнитного потока через замкнутый контур, в который входит проводник.

Данная формула универсальна, хотя мы получили ее в частном случае. Удобство этой формулы состоит в том, что в ряде случаев при вычислении работы можно избежать интегрирования (например, вычисляя работу при повороте рамки с током в магнитном поле).

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

В предыдущих главах было выяснено, что электрическое поле вызывает протекание электрического тока в проводнике и, вследствие этого, приводит к возникновению магнитного поля. Как будет показано ниже, возможны и обратные процессы, при которых магнитное поле порождает поле электрическое. Таким образом, мы придем выводу о взаимной связи электрических и магнитных полей или к понятию электромагнитного поля.