В электромагнитном поле

На заряженную частицу в электромагнитном поле действует сила Лоренца. Поэтому релятивистское уравнения движения для пространственных компонент имеет вид:

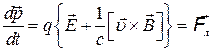(1)

а уравнение для четвертой компоненты дает:

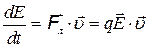
Выразим силу Лоренца 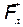через электромагнитный потенциал :

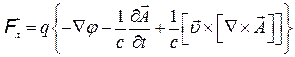(2)

Так как

,

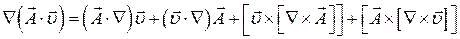а при частном дифференцировании по координате 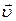надо полагать за постоянную, то

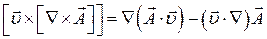
и таким образом

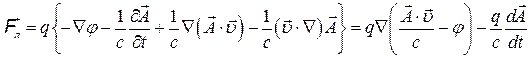
так как

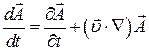
Поэтому (1) примет вид :

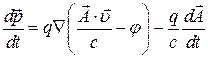(3)

Эти уравнения можно рассматривать, как уравнения Лагранжа если

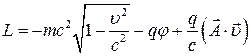(4)

Тогда обобщенный импульс 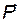и обобщенная сила 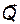по определению равны:

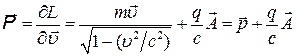(5)

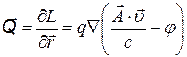(6)

Подставляя (5) и (6) в уравнения Лагранжа:

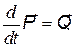(7)

получим (3) . Таким образом, 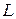(4) – действительно функция Лагранжа.

Внерялитивистском приближении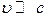

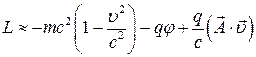, т.е.

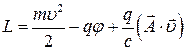(8)

Видно, что даже при 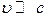функция Логранжа не равняется разности кинетической и поступательной энергии, так как в (8) есть слагаемое зависящее от 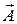и .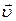

Найдем функцию Гамильтона:

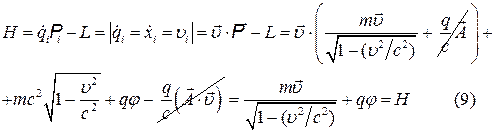
Функция (9) будет функцией Гамильтона, если выразить 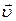через обобщенный импульс .

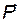Из (9) следует, что :

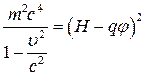(10)

а из (5) находим:

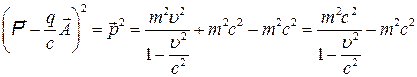
т.е.

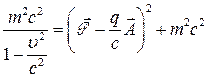(11)

Сравнивая (10) и (11), получим

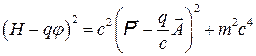
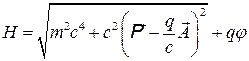(12)

Так как 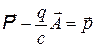, а, с другой стороны в отсутствие магнитного поля (электростатика) 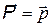и 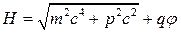(12а), то функция Гамильтона в обоих случаях, по сути дело, совпадают. Это не удивительно: магнитное поле не изменяет энергию частиц.