Вычисление моментов линии ядерного магнитного резонанса

Цель работы:Ознакомление с теорией моментов линий ЯМР. Съемка спектра ЯМР образца твердого тела. Вычисление второго и четвёртого моментов из записанного спектра. Идентификация формы полученного спектра по рассчитанным моментам. Теоретический расчет второго момента и сравнение его со вторым моментом, полученным из обработки экспериментального спектра.

Приборы и принадлежности: Спектрометр ЯМР широких линий, образец твердого полиметилметакрилата (ПММА).

ТЕОРИЯ

При учёте диполь-дипольного взаимодействия в системе с большим количеством ядер теоретический расчёт спектров ЯМР оказывается практически невозможным. Тем не менее, некоторые параметры линии поглощения можно легко вычислить, используя теорию моментов Ван-Флека. Наибольшее значение имеет второй момент, представляющий собою среднеквадратичную ширину линии.

Рассмотрим функцию f(w) – функция формы линии, которая определяется следующим выражением:

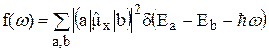. (1)

Определим теперь n-е моменты функции f(w) выражениями

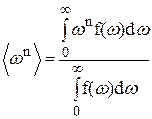(2)

и

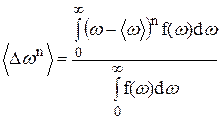. (3)

Выражение (3) для n=2 называется вторым моментом. Очевидно, момент 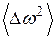по порядку величины равен квадрату ширины линии, так что

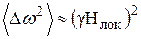. (4)

Определяемые выражениями (2) и (3) моменты тесно связаны друг с другом. Эту связь в случае n=2 можно установить следующим образом. Выписывая 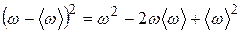и учитывая (2) и (3), получаем

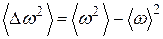. (5)

Очевидно, величину 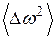можно рассчитывать либо непосредственно, либо выражать её через предварительно вычисленные значения 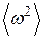и 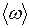. Мы воспользуемся последним способом.

В качестве иллюстрации общего метода расчета вычислим сначала интеграл 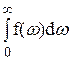, пропорциональный площади, ограниченной кривой поглощения. Затем мы вычислим величины 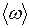и 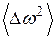. Поскольку функция f(w) является чётной функцией,

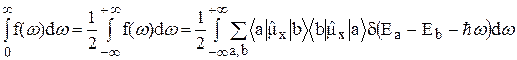. (6)

Вследствие наличия d-функции в подынтегральном выражении этот интеграл отличен от нуля только в том случае, когда 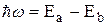. Но для любой пары состояни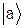й и 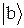имеется некоторое значение w в области между 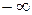и 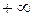, которое удовлетворяет условия 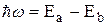. Отметим, что при интегрировании от 0 до 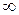в интеграл не давали бы вклада состояния, для которых величина 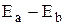отрицательна. По этой причине область интегрирования была распространена на всю область изменения частоты от 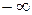до 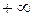. Заменяя переменную интегрирования w на 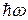, получаем

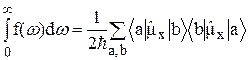. (7а)

Применяя основную теорему квантовой механики

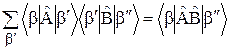, (7б)

справедливую для произвольных операторов 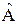и 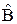и для любого полного набора функций 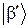, находим

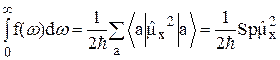. (8)

Другая важная теорема утверждает, что при замене полного набора ортогональных функций 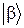другим полным набором функций 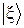(функции 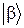могут быть представлены в виде линейных комбинаций функций 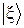) величина следа не меняется. Поэтому для вычисления следа можно пользоваться любым полным набором функций. Выберем в качестве такого набора произведения N собственных функций отдельных спинов, собственные квантовые числа которых равны m₁, m₂,…, m_N. Тогда

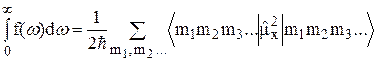. (9)

Отсюда при учёте равенства 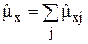находим

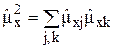. (10)

В этом выражении содержатся члены двух типов 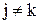с и с 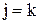. Рассмотрим сначала члены первого типа. Положим j=1, k=2. Фиксируя значения m₂, m₃, m₄, получаем

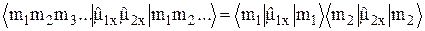, (11)

или после суммирования по m₁

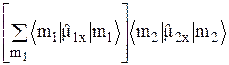. (12)

Но 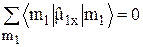. В этом можно убедиться, если заметить, что функции 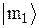являются собственными функциями оператора 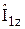, а диагональные матричные элементы операторов 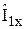и 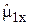, вычисленные с этими волновыми функциями, равны нулю. В противоположность такому выбору в качестве собственных значений m₁ можно было бы выбрать собственные значения операторов 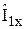. Но тогда каждому значению +m будет соответствовать точно такое же отрицательное значение, что даёт

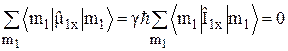. (13)

Таким образом, вклад от членов с 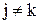будет равен нулю. Для членов с 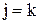, полагая j=1, находим

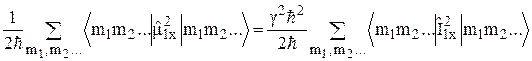. (14)

Входящий в это выражение матричный элемент не зависит от m₂, m₃ и т. д. Поэтому сумма будет состоять из множества одинаковых слагаемых. Так как имеется (2I+1) квантовых чисел m₂, (2I+1) квантовых чисел m₃ и т. д., то матрица, матричные элементы которой зависят от m₁, будет встречаться при суммировании (2I+1)^N-1 раз. С другой стороны, учитывая, что символ Sp₁ обозначает след по квантовым числам спина 1, находим 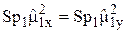. Это равенство легко проверить непосредственным вычислением. С помощью собственных функций оператора 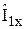находим

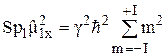. (15а)

Применяя собственные функции оператора 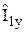, можно найти аналогично

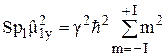. (15б)

Следовательно

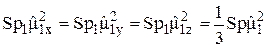. (15в)

Оператор 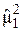имеет (2I+1) диагональный матричный элемент, каждый из которых равен 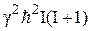. Поэтому

.

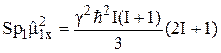Учитывая, что имеется N одинаковых членов с 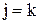, получаем

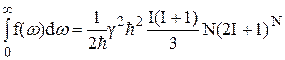. (16)

Вычислим теперь изменение средней частоты линии поглощения 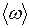, обусловленное дипольным взаимодействием. Существование такого сдвига средней частоты предполагает, что создаваемые соседними магнитными моментами локальные магнитные поля направлены преимущественно параллельно приложенному полю. Этот эффект связан с лоренцевым локальным полем 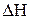, которое должно быть равно по порядку величины 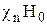, где 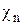– статическая магнитная восприимчивость ядер. Величину 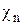можно определить по формуле Ланжевена-Дебая

,

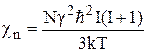где N – число ядер в единице объёма. Если расстояние между ближайшими ядрами равно а, то 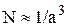. Следовательно,

.

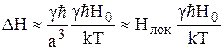Этой величиной в большинстве случаев можно пренебречь, так как она очень мала по сравнению с шириной линии H_лок вследствие того, что зеемановская энергия ядра 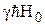во много раз меньше величины kT. Физический смысл полученного выражения для 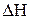состоит в том, что магнитные моменты соседних ядер, хотя и в слабой степени, но всё же ориентируются преимущественно параллельно постоянному полю, входящему в аргумент больцмановского множителя 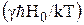. Среднее значение H_лок отличается от нуля на величину 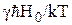. Вычисленные с помощью равенства (1) величины 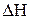и 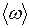должны равняться 0 и w₀ соответственно, поскольку (1) соответствует случаю бесконечно большой температуры.

Строгое вычисление средней частоты, или первого момента

,

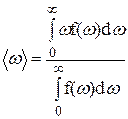представляет собой более сложную задачу, чем вычисление интеграла 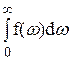. В (6) удобно было перейти к интегрированию от 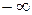до 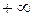. После такого изменения пределов интегрирования каждой паре уровней энергии всегда можно было сопоставить такое значение частоты w, чтобы равенство 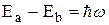выполнялось как для положительных, так и для отрицательных значений 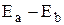. В выражении для величины 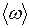такого преобразования сделать нельзя, так как

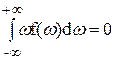(17)

вследствие нечётности подынтегральной функции. Поэтому мы вынуждены вычислять :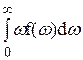

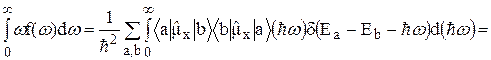
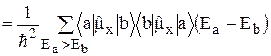. (18)

Как было отмечено выше, энергии E_a и E_b равны суммам зеемановских и дипольных вкладов 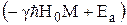. Предположим, что при приводящих к поглощению переходах изменение дипольной энергии всегда много меньше изменения зеемановской энергии, соответствующего поглощению на частоте, равной примерно w₀. Поскольку E_a>E_b , мы можем написать

,

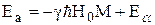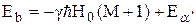(19)

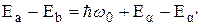
С помощью этих соотношений перепишем равенство (18) в виде

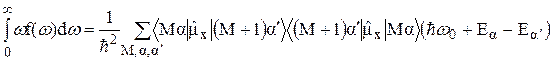. (20)

Рассмотрим сначала в этом выражении член, пропорциональный :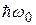

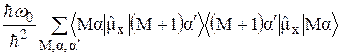. (21)

Это выражение можно было бы записать в виде следа, если бы не была фиксирована величина M+1. От этого ограничения можно избавиться, если воспользоваться свойствами повышающих и понижающих операторов и учесть равенство

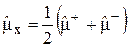. (22)

Тогда

.

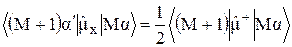Поскольку оператор 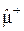, связывающий состояния 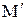и M, имеет отличные от нуля матричные элементы 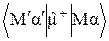только для переходов, при которых выполняется условие 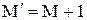, выражение (21) можно записать в форме, где суммирование проводится по всем значениям величины :

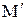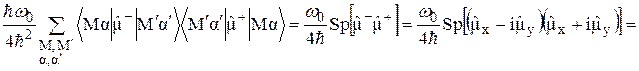
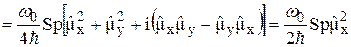. (23)

Здесь мы воспользовались равенствами 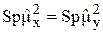и

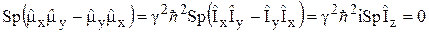(24)

До сих пор рассматривался только член в (20), пропорциональный 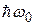. Легко рассмотреть член этого равенства, пропорциональный 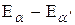. Известно, что 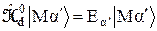. Поэтому для произвольного оператора 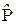справедливо равенство

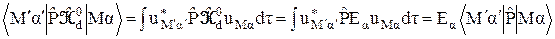. (25)

При учёте эрмитовости оператора 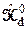далее находим

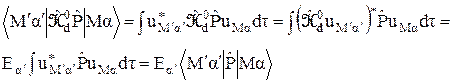(26)

Поэтому

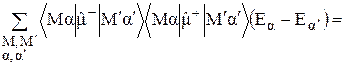
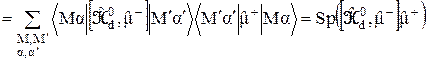. (27)

Детальное вычисление следа в (27) показывает, что он равен нулю. Поэтому из (20), (23) и (27) получаем

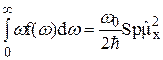. (28)

Но, согласно (8),

,

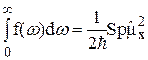поэтому

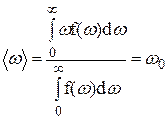(29)

Следовательно, среднее значение частоты не изменяется в присутствии дипольного взаимодействия.

Для вычисления упомянутой выше поправки, обусловленной локальным полем, необходимо было бы вернуться к выражению (1) и включить в него экспоненциальный множитель, опущенный в (1). (Необходимость включения такого множителя вытекает из того, что выражение 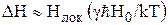зависит от температуры, а в выражение (1) температура входит только через экспоненциальный множитель.)

Второй момент 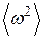можно вычислить аналогичным образом:

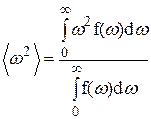. (30)

В выражении (30) необходимо вычислить только числитель, так как знаменатель уже вычислен выше:

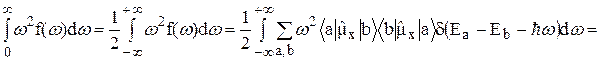
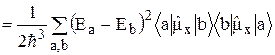. (31)

Так же, как это было сделано при выводе равенств (26) и (27), при учёте уравнения 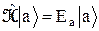находим

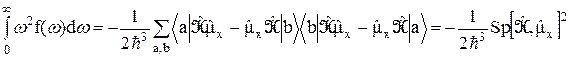. (32)

Учитывая, что 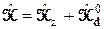, далее получаем

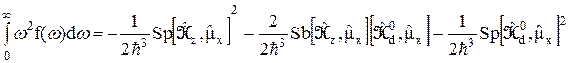. (33)

Здесь при преобразовании перекрёстных членов, включающих операторы 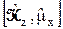и 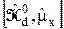, было использовано справедливое для пары любых операторов 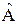и 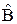равенство

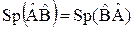, (34)

которое легко проверить при помощи (7б).

Если исключить из рассмотрения дипольное взаимодействия, то в правой части равенства (33) остаётся только первый член и величина 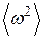будет равна 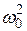. В этом случае форма линии будет описываться 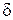-функцией. Точный расчёт подтверждает этот вывод. Второй, или «перекрёстный», член в правой части (33) равен нулю в силу того, что он содержит множитель 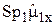. Последний член в правой части (33), делённый на 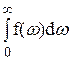, даёт

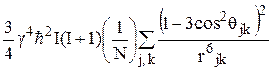. (35)

Отсюда с помощью (5)

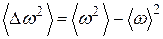
и с учётом равенства 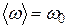получаем

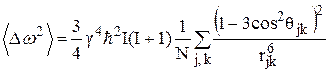. (36)

Для того чтобы вычислить второй момент необходимо выбрать какое-либо ядро и просуммировать относительно него r_ik и θ_ik в соответствии с уравнением. Однако на практике из-за того, что 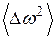~r_ik^-6 суммирование можно ограничить ближайшими соседями, где r_ik – составляет несколько межатомных расстояний, а остальную часть исследуемого вещества представить в виде сплошной среды. Суммирование при этом заменяется интегрированием.

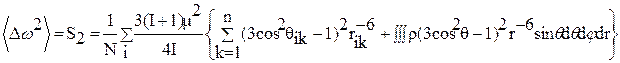, (37)

где n – число ядер k в сфере радиусом r₀, ρ – число ядер в единице объёма.

В поликристаллах и аморфных веществах усреднение по углам θ_ik даёт

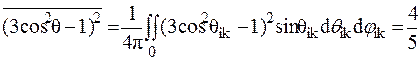, (38)

и, следовательно

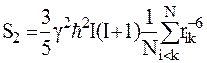(39)

При наблюдении сигналов ЯМР в твёрдых телах, характеризующихся большой шириной и малой амплитудой, используется дифференциальное прохождение сигнала ЯМР, при котором записывается производная линии поглощения (рис. 1).

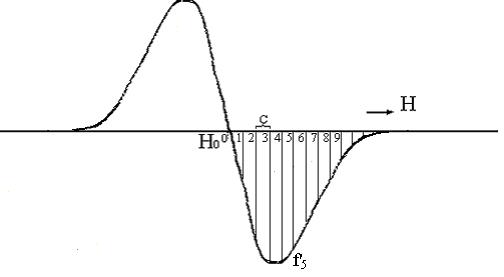
Рис. 1. Производная линии поглощения ЯМР

Преимуществом дифференциального прохождения является то, что при этом значительно сужается полоса пропускания радиоэлектронной аппаратуры до 0,01 Гц, а, следовательно, существенно повышается отношение сигнал/шум – основной показатель чувствительности спектрометров ЯМР. Немаловажно также и то, что производная линии поглощения более чувствительна к изменению формы кривой. Кривые поглощения в твёрдых телах описываются функциями, близкими к гауссовой или лоренцевой, либо занимающими промежуточное значение.

Для производной линии поглощения f^’(H)

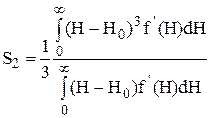(40)

В практических целях интегрирование заменяется суммированием путём разбиения линии или её производной на равностоящие отрезки (рис. 1). Тогда

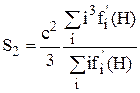, (41)

где с – цена деления (в ).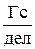

Аналогичные формулы можно записать для площади под кривой и четвёртого момента

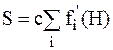(42)

и

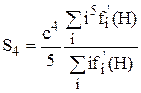(43)

Форма линии ЯМР определяется отношением четвёртого момента к квадрату второго

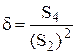(44)

Для гауссовой кривой δ=3, для лоренцевой δ>>3 и зависит от точки обрезания лоренцевой кривой (для необрезанной лоренцевой кривой понятие указанных моментов неприменимо).

Площадь под кривой, определяемая по формуле (42) пропорциональна количеству ядер данного типа в исследуемом веществе.

Истинное значение второго момента линии поглощения ЯМР получается при вполне определённых экспериментальных данных. Наиболее существенное влияние на значение S₂ оказывает амплитуда модуляции R_m, уровень генерации ВЧ-поля (отсутствие насыщения), скорость прохождения резонансных условий v и постоянная синхронного детектора t₀.

Не всегда можно устранить влияние этих факторов, ибо их устранение часто приводит к уменьшению сигнала ЯМР. Поэтому приходится учитывать влияние этих экспериментальных факторов, вычисляя истинное значение вторых моментов.

Так, влияние амплитуды модуляции учитывается в виде:

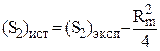, (45)

а скорость прохождения и постоянные синхронного детектора:

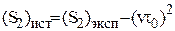(46)

Слишком большие амплитуды модуляции, превышающие полуширину линии, приводят к уменьшению интенсивности линий и увеличению погрешности.нанных. второго момента линии поглощения ЯМР получается при вполне определённых эксперементальных дуемом ния радиоэлектрон

В данной лабораторной работе исследуется форма линии в полимерном образце твердого аморфного полиметилметакрилата (ПММА). Мономерное звено молекулы полиметилметакрилата имеет вид

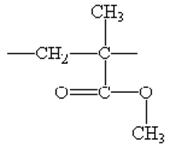
Поскольку исследуемый образец аморфный, к нему применим подход вычисления второго момента для порошковообразного образца (формула (39)). Если учитывать взаимодействия между протонами только внутри CH₂ и CH₃ групп, то выражение для второго момента полиметилметакрилата записывается в виде

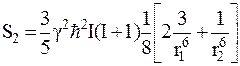, (47)

где I=1/2, 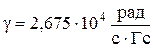, , ,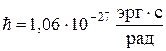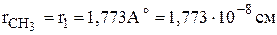