Определение систематической погрешности
Результата измерения
Систематическая погрешность определяется на основе выражений (2.2), (2.4), (2.5) в двух режимах измерения: статическом и динамическом.
Статический режим измерения
Под статическим режимом измерения понимается такой режим измерения, при котором влияние инерционных свойств СИ на погрешность результата измерения пренебрежимо мало. При таком допущении можно принять 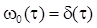 и уравнения (2.2) и (2.5) записать в следующем виде
и уравнения (2.2) и (2.5) записать в следующем виде
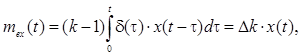 (2.7)
(2.7)
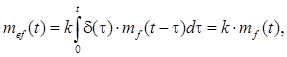 (2.8)
(2.8)
Из выражения (2.7) следует, что мультипликативная погрешность возникает из-за того, что Dk = k – 1 ≠ 0, то есть из-за того, что СИ воспроизводит единицу величины не точно.
Пример 2.1. Пусть 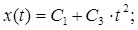 С1 =10 В; С3 =0,1 В×с-2; Dk =0.01;
С1 =10 В; С3 =0,1 В×с-2; Dk =0.01;  В. Тогда на основе уравнений (2.7), (2.8) и (2.4) получим
В. Тогда на основе уравнений (2.7), (2.8) и (2.4) получим
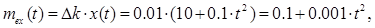
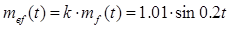 ,
,
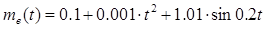 .
.
Графики мультипликативной, аддитивной и суммарной систематических погрешностей представлены на рис. 2.1.
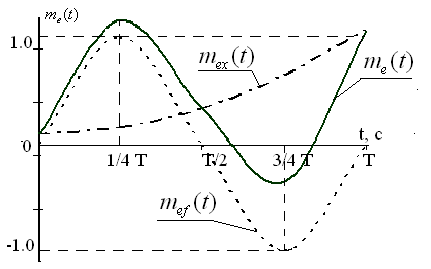
Рис. 2.1. Графики мультипликативной, аддитивной и суммарной систематических погрешностей в статическом режиме
Динамический режим измерения
Под динамическим режимом измерения понимается такой режим измерения, при котором влиянием инерционных свойств СИ на погрешность результата измерения пренебречь нельзя. При таком допущении 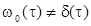 и, следовательно, определение мультипликативной погрешности сводится к интегрированию выражений (2.2) и (2.5).
и, следовательно, определение мультипликативной погрешности сводится к интегрированию выражений (2.2) и (2.5).
Для случая 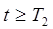 (установившееся состояние СИ) и существования производных
(установившееся состояние СИ) и существования производных 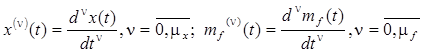 , выражения (2.2) и (2.5) могут быть представлены конечными суммами следующего вида
, выражения (2.2) и (2.5) могут быть представлены конечными суммами следующего вида
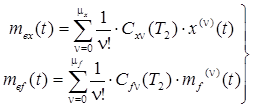 (2.9)
(2.9)
где 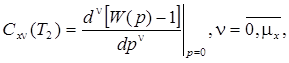

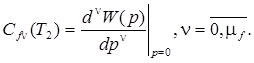
Пример 2.2. Пусть 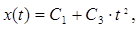 С1=10 В, С3=0,1 В×с-2, Dk = 0,01. Передаточная функция СИ равна
С1=10 В, С3=0,1 В×с-2, Dk = 0,01. Передаточная функция СИ равна
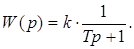
Требуется определить систематическую мультипликативную погрешность.
Решение:
Из выражения (2.9) имеем
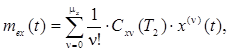
где 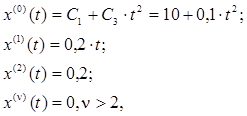
следовательно, mx = 2.
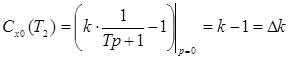 ;
;
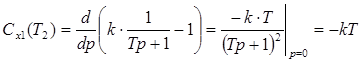 ;
;
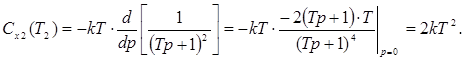
Используя полученные выражения, будем иметь
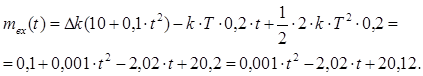
Приравнивая правую часть этого выражения нулю
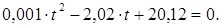
Корни этого уравнения равны
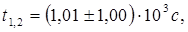
Таким образом, получим
t1=10 c, t2=2010 c.
Графическое изображение функции mex(t) на интервале [t1, t2] представлено на рис. 2.2.
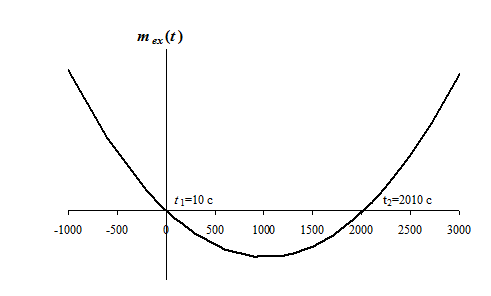
Рис. 2.2. График систематической мультипликативной погрешности в динамическом режиме
Определение дисперсии случайной погрешности
Результата измерения
Согласно структурной схеме формирования погрешн6ости, приведенной на рис. 1.1, центрированная случайная составляющая погрешности Е(t) обусловлена центрированным случайным возмущением F(t), характеризующимся спектральной плотностью Sf(w). Уравнения, связывающие случайные функции Е(t)и F(t), представлены выражением (2.6). Однако, это выражение не приспособлено для практического использования при определении характеристик случайной погрешности. Более предпочтительным является выражение, связывающее непосредственно спектральные плотности погрешности и случайного возмущения, а именно
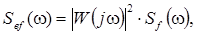 (2.16)
(2.16)
где 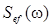 – спектральная плотность аддитивной погрешности Еf(t),
– спектральная плотность аддитивной погрешности Еf(t),
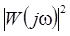 – квадрат модуля частной характеристики СИ.
– квадрат модуля частной характеристики СИ.
В свою очередь, спектральная плотность определяет такую важную числовую характеристику случайной погрешности как дисперсия. Выражение для дисперсии имеет следующий вид
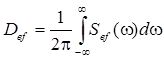 .
.
После подстановки выражения (2.16) получим
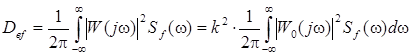 (2.17)
(2.17)
В случае, если спектральная плотность Sf(w) выражается дробно-рациональной четной функцией, то интеграл
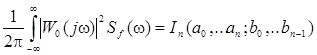 , (2.18)
, (2.18)
где ak, k 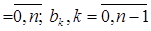 - коэффициенты полиномов по jw соответственно знаменателя и числителя следующего выражения
- коэффициенты полиномов по jw соответственно знаменателя и числителя следующего выражения
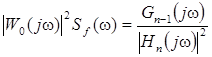 , (2.19)
, (2.19)
где 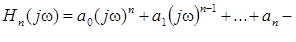 полином степени n,
полином степени n,
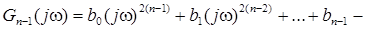 полином степени не выше 2×(n – 1).
полином степени не выше 2×(n – 1).
Выражение для интегралов при n = 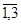 имеют следующий вид
имеют следующий вид
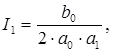
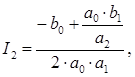

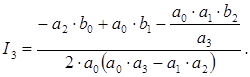
Таким образом, с учетом выражения (2.18) уравнение (2.17) запишется следующим образом
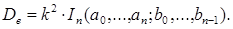 (2.20)
(2.20)
Пример 2.3. Положим k = 1,01
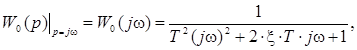
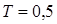 с, x = 0,6,
с, x = 0,6,
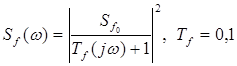 с,
с, 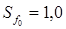 В×с1/2
В×с1/2
На основе уравнения (2.18) получим
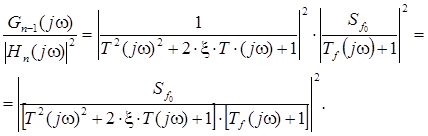
Из этого соотношения следует, что
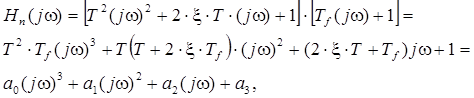
где n = 3, 
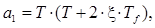
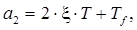 a3 =1,
a3 =1, 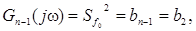
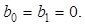
Для n = 3 имеем
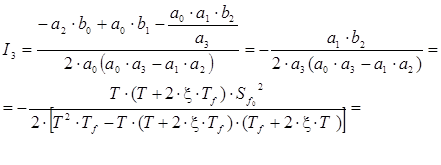
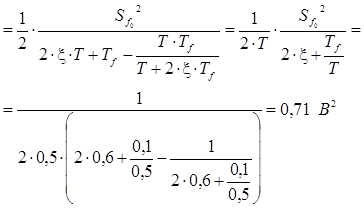
Используя выражение (2.17) получим
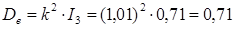 В2.
В2.
Заметим, что найденное значение дисперсии характеризует погрешность результата измерения для условия 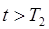 .
.
