Пропорциональное безинерционное (масштабное) звено
Безинерционным звеном называется звено, не обладающее запаздыванием, у которого выходная величина точно следует за входной и пропорциональна ей.
Для безинерционного звена зависимость между входной и выходной величинами выражается формулой
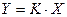 , (3.2)
, (3.2)
где K - коэффициент передачи.
Передаточная функция
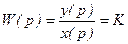 , (3.3)
, (3.3)
Примером простейшего пропорционального звена может служить потенциометр (рисунок 3.1,а). Передаточная функция которого:
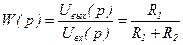 , (3.4)
, (3.4)
Безинерционным пропорциональным звеном можно считать также операционный усилитель (рисунок 3.1,б), у которого на входе и в обратной связи включены активные сопротивления, то есть Z0(p)=R0, Z1(p)=R1. Передаточная функция такого усилителя:
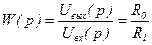 , (3.5)
, (3.5)
Комплексный коэффициент усиления:
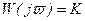 , (3.6)
, (3.6)
Амплитудно-фазовая частотная характеристика (рисунок 3.1,в) представляет собой точку, отстоящую по оси абсцисс на расстоянии K от начала координат.
Амплитудно-частотная характеристика:
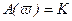 , (3.7)
, (3.7)
Фазовая частотная характеристика
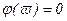 , (3.8)
, (3.8)
АЧХ и ФЧХ показаны соответственно на (рисунок 3.1,г, д), из которых следует, что безинерционное звено пропускает все частоты без сдвига по фазе.
Логарифмическая амплитудно-частотная характеристика
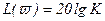 , (3.9)
, (3.9)
Переходная функция
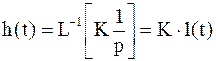 , (3.10)
, (3.10)
Весовая функция
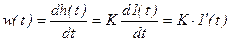 , (3.11)
, (3.11)
ЛАХ, переходная и весовая функции показаны соответственно на рисунке 3.1,е,ж,з.
Интегрирующее звено
Интегрирующим называют звено, у которого выходная величина пропорциональна интегралу от входной величины.
Дифференциальное уравнение интегрирующего звена
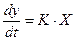 , (3.12)
, (3.12)
Ему равноценно интегральное уравнение
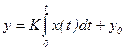 , (3.13)
, (3.13)
где K - коэффициент пропорциональности.
Электрический конденсатор можно рассматривать как интегрирующее звено, если за выходную величину рассматривать напряжение (рисунок 3.2,а).
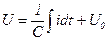 , (3.14)
, (3.14)
Передаточная функция интегрирующего звена имеет вид
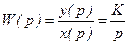 , (3.15)
, (3.15)
Комплексный коэффициент усиления
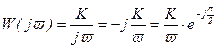 , (3.16)
, (3.16)
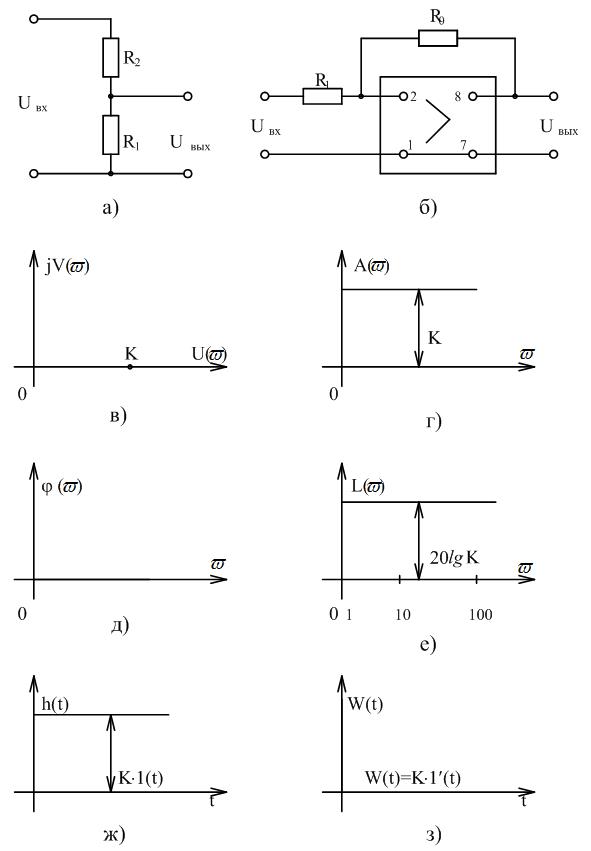
Рисунок 3.1 Характеристики пропорционального звена
Амплитудная частотная характеристика
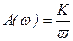 , (3.17)
, (3.17)
Фазовая частотная характеристика
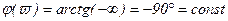 , (3.18)
, (3.18)
АФХ, АЧХ и ФЧХ построены согласно формулам (3.16)-(3.18) и показаны соответственно на (рисунок 3.2,в ,г, д).
Логарифмическая амплитудная характеристика (рисунок. 3.2,е) определяется выражением
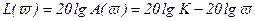 , (3.19)
, (3.19)
Определим наклон ЛАХ интегрирующего звена по отношению к оси абсцисс. Для этого определим ординату ЛАХ при частоте ϖ1=10ϖ.
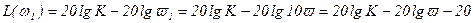 , (3.20)
, (3.20)
Откуда видно, что отношение выходной и входной амплитуд уменьшается на 20 дб при увеличении частоты в 10 раз, то есть ЛАХ имеет наклон - 20 дб на декаду (-20 дб/дек.)
Так при L(ϖ)=0 20lgK=20lgϖ, то ЛАХ пересечет ось абсцисс в точке ϖ =K.
Таким образом, логарифмическая амплитудно-частотная характеристика интегрирующего звена является прямой линией, проходящей с наклоном -20дб/дек через точку на оси абсцисс, соответствующую частоте ϖ =K.
Переходная функция интегрирующего звена
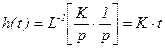 , (3.21)
, (3.21)
Вид этой функции показан на (рисунок 3.2,ж). Отличительная особенность этой функции состоит в том, что она не имеет установившегося (при t®¥) конечного значения. Это свойство обуславливает принципиальное отличие астатических САР, в состав которых входят интегрирующие звенья, от статических, не содержащих эти звенья.
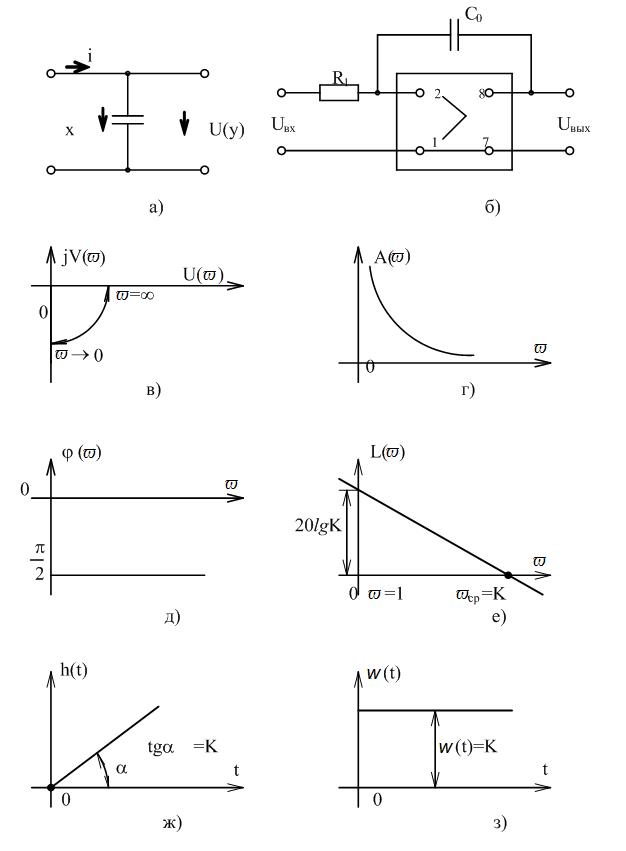
Рисунок 3.2 Характеристики интегрирующего звена
Весовая функция
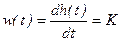 , (3.22)
, (3.22)
Весовая функция интегрирующего звена показана соответственно на рисунке 3.2, з.
Дифференцирующее звено
Дифференцирующим звеном называют такое звено, у которого выходная величина пропорциональна скорости изменения входной величины.
Оно описывается уравнением
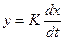 , (3.23)
, (3.23)
Передаточная функция звена
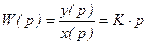 , (3.24)
, (3.24)
Примером такого звена может служить тот же конденсатор, если за выходную величину рассматривать ток в емкости (рисунок 3.3,а).
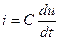 , (3.25)
, (3.25)
Реализовать такое звено на операционном усилителе можно, включив на его входе емкость, а в цепи обратной связи активное сопротивление, то есть 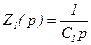 ,
, 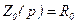 (рисунок 3.3,б). Тогда
(рисунок 3.3,б). Тогда
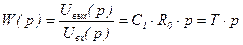 , (3.26)
, (3.26)
Реализовать такую передаточную функцию можно с некоторой погрешностью, так как операционный усилитель при таком включении емкости становится помехоустойчивым.
Комплексный коэффициент усиления
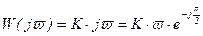 , (3.27)
, (3.27)
Амплитудная и фазовая частотные характеристики:
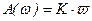 , (3.28)
, (3.28)
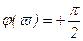 , (3.29)
, (3.29)
Логарифмическая амплитудно-частотная характеристика
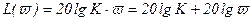 , (3.30)
, (3.30)
Частотные характеристики идеального дифференцирующего звена, построенные в соответствии с формулами (3.23)-(3.30), показаны соответственно на рисунке 3.3, в, г, д, е.
На рисунке 3.3,е видно, что ЛАХ идеального дифференцирующего звена представляет собой прямую с угловым коэффициентом +20дб/дек.
Переходная функция
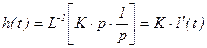 , (3.31)
, (3.31)
представляет собой бесконечно тонкий импульс с площадью K. Переходная функция идеального дифференцирующего звена показана на рисунке 3.3, ж.
Все остальные звенья САУ являются производными от рассмотренных выше простейших звеньев. Рассмотрим это на примере звеньев первого и второго порядка.
