Оцінка областей визначення та множини значень. Монотонність. Опуклість

При доведенні нерівностей в окремих випадках доцільно проаналізувати область визначення та множину значень заданих в умові виразів. Цього іноді може виявитися достатньо для розв’язання задачі.

Задача2.1.1. Довести нерівність

.

Доведення. Нема потреби робити певні перетворення при доведенні даної нерівності. Достатньо, порівнюючи підкореневі вирази, побачити, що при довільних 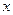та виконується нерівність . Тому ліва частина приймає значення менші, ніж права.

Задача2.1.2. При довести нерівність

.

Доведення. Очевидно, що

, , .

Тому ліва частина виразу приймає значення більші або рівні 1. Отже, нерівність виконується на всій області допустимих значень, тобто при . Знак рівності досягається при .

Задача2.1.3. Довести нерівність

.

Доведення. Проаналізуємо область визначення виразу. Для його лівої частини вона визначається системою нерівностей

з єдиним розв’язком . При знайденому значенні ліва частина нерівності набуває значення 2. Залишається зауважити, що в правій частині нерівності є сума двох обернених чисел, яка не менша 2. Знак рівності досягається при .

Задача 2.1.4. Довести нерівність

.

Доведення. Насамперед зауважимо, що ліва частина нерівності визначена на проміжку і, монотонно зростаючи на цьому проміжку, приймає найменше значення у точці . Це значення дорівнює 2. Записавши праву частину нерівності у виді , бачимо, що значення цього виразу не перевищують 2, причому рівність двом досягається в єдиній точці . Порівнюючи множини значень обох частин заданого виразу, робимо висновок, що рівність можлива тільки при . Для інших значень змінних нерівність буде строгою.

Задача 2.1.5. Довести, що на всій області визначення виразу виконується нерівність

,

де кількість радикалів – довільне число .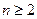

Доведення. Очевидно, що структура виразу дозволяє суттєво спростити його, використовуючи перетворення лівої частини за допомогою співвідношення

.

Ми виберемо інший підхід, який є простішим. Побачивши, що вираз монотонно зростає на всій своїй області визначення , знаходимо його найменше значення. Воно, як легко бачити, при дорівнює . Цим самим нерівність доведена.

При доведенні деяких нерівностей використовуються властивості опуклих функцій. Зокрема, якщо функція 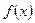на відрізку опукла вгору, то для двох довільних різних точок 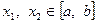виконується нерівність 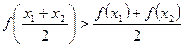. Якщо ж функція 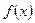на відрізку опукла вниз, то для двох довільних різних точок 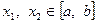виконується нерівність 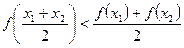. Наведемо приклади.

Задача 2.1.6. Порівняти числа:

а) та ,

б) та .

Розв’язання. У випадку а) розглянемо функцію , яка є опуклою вниз. Тому, використавши нерівність 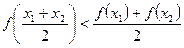, дістаємо, що

.

У випадку б) розглядаємо функцію , яка є опуклою вгору. Використавши нерівність 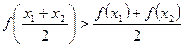, дістаємо .

Задача 2.1.7. Числа 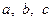задовольняють нерівності

, , .

Довести, що всі вони додатні.

Доведення. Насамперед зауважимо, що числа 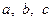є коренями кубічного рівняння

.

Очевидно, що для від’ємних 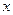ліва частина рівняння приймає від’ємні значення. Отже, корені можуть бути тільки додатними, що завершує доведення.

В окремих випадках у залежності від постановки задачі доцільно досліджувати необхідні умови. Наприклад, необхідною умовою того, щоб рівняння мало два корені, сума яких більша 2, а добуток був більший 3, відповідно до теореми Вієта, є виконання системи нерівностей . У даному випадку система несумісна і поставлена задача розв’язків не має. Але, якщо ми цю ж задачу сформулюємо для рівняння і отримаємо систему із розв’язками , то одержаної нерівності ще не достатньо, щоб вважати задачу розв’язаною. Обов’язково потрібно врахувати умову існування коренів у вигляді нерівності . Звідси, оскільки , отримуємо .

Зауважимо, що відшукання необхідних умов не є обов’язковим етапом розв’язування задач. Наприклад, при розв’язуванні нерівності нема потреби займатися знаходженням її області визначення, оскільки нерівність рівносильна заданій.

Розглянемо подібну до попередньої наступну задачу.

Задача2.1.8. При яких значеннях параметра 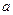рівняння має два корені, які обидва більші від 1?

Помилковий розв’язок, запропонований авторами даної задачі в одному із навчальних посібників, виглядає так. Умова задачі рівносильна системі нерівностей

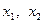( - корені рівняння),

звідки, оскільки перша нерівність системи виконується (сума коренів дорівнює 4), а друга записується у виді , отримуємо розв’язок .

Помилка у наведених міркуваннях полягає у тому, що записана система виражає необхідну, але не достатню умову того, що обидва корені більші від 1. Адже, щоб добуток двох чисел був більший 1, зовсім не обов’язково, щоб кожне з них перевищувало 1. Правильний розв’язок може виглядати наступним чином. Оскільки абсциса вершини параболи дорівнює 2 і розташована правіше точки , то для відшукання розв’язку задачі достатньо вимагати, щоб виконувалися умови та . Розв’язавши систему нерівностей , отримуємо .

Задача 2.1.9.При яких значеннях параметр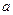а точка є точкою екстремуму функції ?

Розв’язання. Згідно з умовою задачі, похідна у точці повинна перетворюватись у 0. Це дозволяє отримати значення 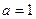. Проте, як легко переконатися, функція у точці екстремуму не має.

Отже, точка при жодному значенні параметра 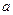не може бути точкою екстремуму заданої функції.

Задача 2.1.10.При яких значеннях параметра 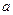сума квадратів коренів рівняння буде найменшою?

Розв’язання. За теоремою Вієта . Тоді

,

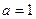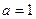але стверджувати, що значення , при якому одержаний вираз приймає мінімальне значення, є шуканим, ще рано. Потрібно додатково дослідити умову існування дійсних коренів. Знаходимо , звідки та . Як бачимо, число одержаним інтервалам не належить. Тому, оскільки на знайдених інтервалах функція монотонна, мінімальне значення виразу буде в одній із точок . Очевидно, що такою точкою є .