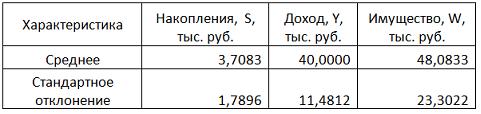
По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице

Построена матрица парных коэффициентов корреляции

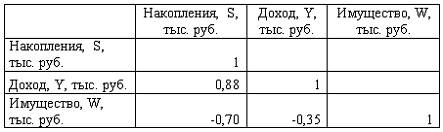
Тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии, характеризует …

частный коэффициент корреляции

коэффициент парной корреляции между фактором и результатом

частный F-критерий Фишера

коэффициент эластичности

Решение:

Частный коэффициент корреляции характеризует тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Коэффициент парной корреляции между фактором и результатом характеризует тесноту связи между фактором и результатом без устранения влияния других факторов, включенных уравнение регрессии.
С помощью частного F-критерия Фишера можно проверить все коэффициенты регрессии в предположении, что соответствующий фактор был введен в уравнение регрессии последним.

В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.

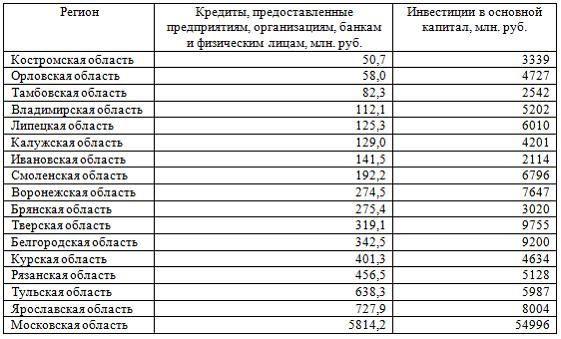
По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R² = 0,9708.

В уравнении, параметры которого являются значимыми, коэффициент ____________ показывает, на сколько единиц измерения изменится зависимая переменная у, если независимая переменная x увеличится на 1 единицу измерения.

регрессии

корреляции

детерминации

эластичности

Решение:

Правильный ответ – коэффициент регрессии, он в уравнении, параметры которого являются значимыми, показывает, на сколько единиц измерения изменится зависимая переменная у, если независимая переменная x увеличится на 1 единицу измерения.

Коэффициент корреляции характеризует тесноту связи между переменными.

Коэффициент детерминации – долю дисперсии, объясненной регрессией в общей дисперсии.

Коэффициент эластичности в уравнении, параметры которого являются значимыми, показывает, на сколько процентов изменится зависимая переменная у, если независимая переменная x увеличится на 1 процент.

Кейс 1 подзадача 2

1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.

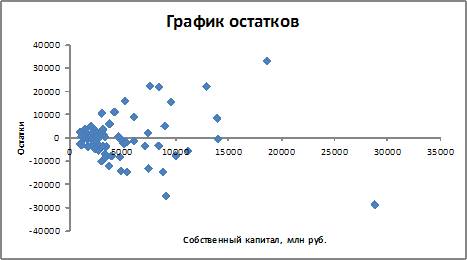
Проанализировав график остатков, можно сделать вывод о том, что выполняются предпосылки метода наименьших квадратов о …

случайном характере остатков

нулевой средней величине остатков

гомоскедастичности остатков

нормальном распределении остатков

Решение:

Исследования остатков e_i предполагают проверку пяти предпосылок метода наименьших квадратов:

1) случайный характер остатков;

2) нулевая средняя величина остатков, не зависящая от x_i;

3) гомоскедастичность остатков – дисперсия каждого отклонения e_i одинакова для всех значений x_i;

4) отсутствие автокорреляции остатков (значения остатков e_i распределены независимо друг от друга);

5) остатки подчиняются нормальному закону распределения.
В данном случае очевидно выполнение предпосылки о случайном характере остатков, на графике в расположении остатков нет направленности, они расположены в форме облака, значит, предпосылка о случайном характере остатков выполняется.

Остатки колеблются около нуля, следовательно, предпосылка о нулевой средней величине остатков также выполняется.

Гомоскедастичность остатков означает, что дисперсия остатков не зависит от независимой переменной. В данном случае, согласно анализу графика остатков, это не так. При небольших значениях x_i величины остатков невелики, при увеличении значений x_i величины остатков также увеличиваются, то есть предпосылка о гомоскедастичности остатков нарушается.

Предпосылки о гетероскедастичности остатков просто не существует.