Спектральное представление колебаний
4.1. Спектры периодических негармонических колебаний
[1, с. 274–279; 2, с. 144–152]
Если колебание описывается периодической функцией f(t),значения которой повторяются через период T и которая удовлетворяет условиям Дирихле, то его можно представить в виде суммы гармонических колебаний с частотами, кратными основной частоте колебания 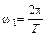 .
.
Такое представление, называемое рядом Фурье, имеет вид
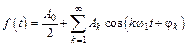 .
.
Комплексные амплитуды гармонических составляющих колебания определяются по формуле
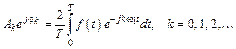
Гармоническое колебание с частотой w1называют первой или основной гармоникой, а колебания с частотами 2 w1, 3 w1, … соответственно второй, третьей и т. д. гармониками. Слагаемое 0,5A0 называется нулевой гармоникой или постоянной составляющей колебания. Оно равно среднему за период значению колебания.
Для периодической последовательности видеоимпульсов прямоугольной формы с параметрами: амплитудой импульсов А, длительностью импульса tи и периодом следования Т ряд Фурье имеет вид
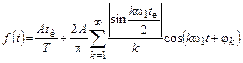 ,
,
если ввести понятие скважности 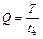 , то
, то
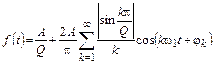 .
.
Закон распределения амплитуд (начальных фаз) составляющих периодического колебания по частоте называют спектром амплитуд (фаз) этого колебания. Периодическое колебание имеет дискретный или линейчатый спектр, так как амплитуды и начальные фазы его гармонических составляющих отличны от нуля лишь при отдельных дискретных значениях частоты, кратных частоте основной гармоники.
4.1.0. Покажите, как изменятся периодическая последовательность видеоимпульсов напряжения и ее спектр амплитуд по сравнению с заданными (рис. 4.1), если период следования T импульсов увеличить в 1,5 раза.
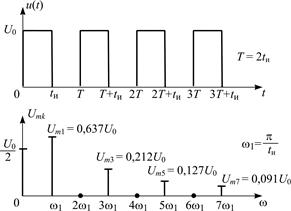
Рис. 4.1
В задачах 4.1.1–4.1.25 покажите, как изменятся периодическая последовательность видеоимпульсов напряжения и ее спектр амплитуд по сравнению с заданными (рис. 4.1), если параметры последовательности видеоимпульсов изменить, как показано в табл. 4.1.
Нарисуйте в одном и том же масштабе заданные последовательность видеоимпульсов и ее спектр амплитуд (рис. 4.1) и рассчитанные для своего варианта.
Таблица 4.1
| Вариант | Изменение параметров последовательности видеоимпульсов |
| 4.1.1 | Длительность импульсов уменьшить в 2 раза, не изменяя периода следования |
| 4.1.2 | Увеличить в 2 раза период следования, длительность и высоту импульсов |
| 4.1.3 | Длительность импульсов уменьшить, а высоту увеличить в 3 раза |
| 4.1.4 | Период следования и высоту импульсов увеличить, а длительность уменьшить в 2 раза |
| 4.1.5 | Период следования и длительность импульсов уменьшить в 2 раза |
| 4.1.6 | Период следования и длительность импульсов увеличить, а высоту уменьшить в 3 раза |
| 4.1.7 | Период следования импульсов увеличить, а длительность уменьшить в 2 раза |
| 4.1.8 | Период следования импульсов увеличить, а высоту уменьшить в 2 раза |
| 4.1.9 | Период следования и высоту импульсов увеличить в 2 раза |
| 4.1.10 | Период следования и длительность импульсов увеличить в 3 раза |
| 4.1.11 | Длительность импульсов уменьшить, а высоту увеличить в 1,5 раза |
| 4.1.12 | Период следования и длительность импульсов уменьшить, а высоту увеличить в 3 раза |
| 4.1.13 | Период следования и высоту импульсов увеличить в 3 раза |
| 4.1.14 | Период следования и высоту импульсов увеличить в 2,5 раза |
| 4.1.15 | Период следования увеличить в 1,5 раза, не изменяя длительности импульсов |
| 4.1.16 | Период следования, длительность и высоту импульсов увеличить в 2,5 раза |
| 4.1.17 | Период следования увеличить в 2 раза, а длительность импульсов уменьшить в 1,5 раза |
| 4.1.18 | Период следования увеличить в 3 раза, а длительность и высоту импульсов увеличить в 2 раза |
| 4.1.19 | Период следования и длительность импульсов уменьшить в 2,5 раза |
| 4.1.20 | Период следования, длительность и высоту импульсов увеличить в 1,5 раза |
| 4.1.21 | Период следования увеличить в 4 раза, а длительность импульсов увеличить в 2 раза |
| 4.1.22 | Период следования увеличить в 3 раза, а длительность и высоту импульсов увеличить в 1,5 раза |
Окончание табл. 4.1
| Вариант | Изменение параметров последовательности видеоимпульсов |
| 4.1.23 | Длительность импульсов уменьшить в 2,5 раза, не изменяя периода следования |
| 4.1.24 | Период следования и высоту импульсов увеличить в 3 раза, а длительность увеличить в 2 раза |
| 4.1.25 | Период следования увеличить в 4 раза, а высоту импульсов увеличить в 2 раза |
4.2. Анализ негармонических периодических колебаний
в электрических цепях
[1, с. 280–282; 2, с. 152–156]
Негармоническое периодическое воздействие можно представить в виде суммы гармонических колебаний, а реакцию на каждое из этих колебаний можно определить, используя символический метод анализа. Амплитуда реакции цепи на k-ю гармонику Akcos(kw1t + jk)воздействия равна произведению амплитуды этой гармоники Ak на значение амплитудно-частотной характеристики цепи на частоте этой гармоники, т. е. равна Ak|H(jkw1)|. Начальная фаза k-й гармоники реакции цепи равна сумме начальной фазы k-й гармоники воздействия jk и значения фазочастотной характеристики цепи на частоте этой гармоники kw1, т. е. [jk + q(kw1)].
Таким образом, реакция цепи на периодическое воздействие есть сумма реакций на гармонические составляющие этого воздействия:
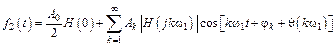 .
.
Как правило, нет надобности определять реакцию цепи на бесконечно большое число гармонических составляющих воздействия, так как амплитуды гармоник убывают с увеличением их номера. В связи с этим в ряде Фурье, которым представляется воздействие, оставляют лишь несколько гармоник, амплитуды которых нельзя считать пренебрежимо малыми по сравнению с амплитудой основной гармоники.
В задачах 4.2.0–4.2.25 найдите реакцию цепи, приведенной в задачах 3.1.0–3.1.25, на периодическое колебание, заданное в виде усеченного ряда Фурье в табл. 4.2. Задающие токи и напряжения источников даны в амперах и вольтах соответственно.
1. Найдите по операторной передаточной функции H(p) задач 3.1.0–3.1.25 комплексную передаточную функцию H(jw) и соответствующие амплитудно-частотную |H(jw)| и фазочастотную Q(w) характеристики цепи.
2. Рассчитайте значения АЧХ и ФЧХ на частотах гармонических составляющих входного колебания.
3. Рассчитайте и запишите реакцию цепи на периодическое воздействие в виде суммы реакций на гармонические составляющие этого воздействия.
4. Постройте графики амплитудно-частотной и фазочастотной характеристик цепи и спектры амплитуд и фаз воздействия и реакции цепи. Оцените влияние цепи на спектры колебания.
Таблица 4.2
| Вариант | Периодическое воздействие, заданное в виде усеченного ряда Фурье |
| 4.2.0 | 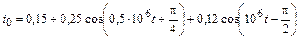 |
| 4.2.1 | 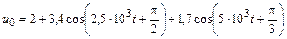 |
| 4.2.2 | 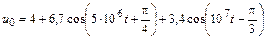 |
| 4.2.3 | 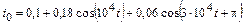 |
| 4.2.4 | 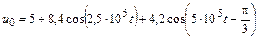 |
| 4.2.5 | 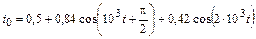 |
| 4.2.6 | 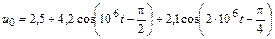 |
| 4.2.7 | 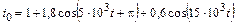 |
| 4.2.8 | 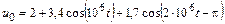 |
Продолжение табл. 4.2
| Вариант | Периодическое воздействие, заданное в виде усеченного ряда Фурье |
| 4.2.9 | 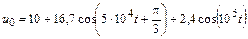 |
| 4.2.10 | 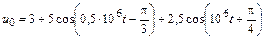 |
| 4.2.11 | 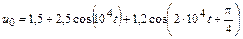 |
| 4.2.12 | 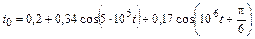 |
| 4.2.13 | 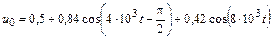 |
| 4.2.14 | 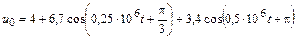 |
| 4.2.15 | 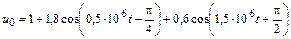 |
| 4.2.16 | 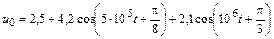 |
| 4.2.17 | 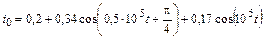 |
| 4.2.18 | 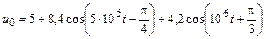 |
| 4.2.19 | 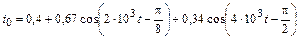 |
| 4.2.20 | 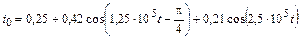 |
| 4.2.21 | 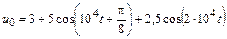 |
| 4.2.22 | 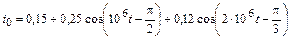 |
Окончание табл. 4.2
| Вариант | Периодическое воздействие, заданное в виде усеченного ряда Фурье |
| 4.2.23 | 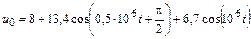 |
| 4.2.24 | 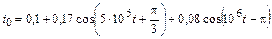 |
| 4.2.25 | 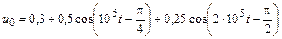 |
4.3. Непериодические колебания. Спектральная плотность.
Влияние амплитудно-частотной характеристики цепи
на спектральную плотность амплитуд воздействия
[1, с. 282–288, 294–299; 2, с. 209–229]
Если непериодическая функция f(t) во всяком конечном промежутке удовлетворяет условиям Дирихле и абсолютно интегрируема в бесконечных пределах, т. е. интеграл 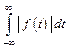 сходится, то такая функция представляется уже не рядом, а интегралом Фурье, который называют обратным преобразованием Фурье
сходится, то такая функция представляется уже не рядом, а интегралом Фурье, который называют обратным преобразованием Фурье
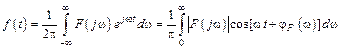 .
.
Таким образом, непериодическое колебание f(t) представляется суммой бесконечно большого числа гармонических колебаний 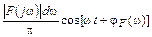 с бесконечно малыми амплитудами
с бесконечно малыми амплитудами 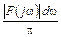 , начальными фазами jF(w) и частотами, изменяющимися от w = 0 до w = ¥. Следовательно, спектр непериодического колебания является непрерывным или сплошным.
, начальными фазами jF(w) и частотами, изменяющимися от w = 0 до w = ¥. Следовательно, спектр непериодического колебания является непрерывным или сплошным.
Прямое преобразование Фурье функции f(t) имеет вид
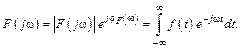
Комплексную величину F(jw) будем называть комплексной спектральной плотностью колебания, ее модуль ½F(jw)½ – спектральной плотностью амплитуд непериодического колебания.
Функция jF(w) = arg F(jw) характеризует спектр фаз непериодического колебания, т. е. частотную зависимость начальных фаз гармонических колебаний бесконечно малых амплитуд, из которых формируется непериодическое колебание.
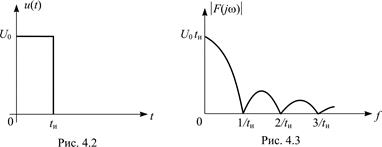
Для прямоугольного видеоимпульса напряжения высотой U0и длительностью tи (рис. 4.2), комплексная спектральная плотность
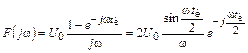 ,
,
где спектральная плотность амплитуд |F(jw)| = 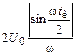 , а ее график представлен на рис. 4.3.
, а ее график представлен на рис. 4.3.
По виду спектральной плотности амплитуд можно судить о том, в какой области частот сосредоточена основная энергия непериодического колебания.
На рис. 4.3 видно, что основная доля энергии прямоугольного видеоимпульса сосредоточена в области нижних частот в пределах главного «лепестка» спектра 0 £ f £ 1/tи. Следует обратить внимание, что чем короче импульс (меньше tи), тем шире его спектр, и наоборот.
Для анализа колебаний в электрических цепях при нулевых начальных условиях и непериодических воздействиях применяется одностороннее преобразование Фурье
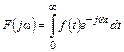 .
.
Тогда по известным комплексной спектральной плотности F1(jw) воздействия и комплексной передаточной функции H(jw) цепи находятся комплексная спектральная плотность искомой реакции
F2(jw) = F1(jw)H(jw)
и ее спектральная плотность амплитуд
|F2(jw)| = |F1(jw)||H(jw)|.
Таким образом, зная АЧХ и ФЧХ цепи, т. е. комплексную передаточную функцию H(jw), можно найти реакцию на любое воздействие, если оно представлено по Фурье. Такой метод анализа переходных колебаний в ЛЭЦ получил название частотного. Метод позволяет оценить частотные искажения в цепях и установить требования к их частотным характеристикам, при выполнении которых электрический сигнал передается цепью без искажений его формы.
4.3.0. Найдите спектральную плотность амплитуд реакции цепи, заданной в задаче 3.1.0, на видеоимпульс тока прямоугольной формы (рис. 3.2, б) для двух значений длительности импульса: tи = 2t и tи = 3t.
Постройте примерные графики АЧХ цепи и спектральных плотностей амплитуд воздействия и реакции для двух значений tи.
Оцените, как длительность импульса влияет на вид спектральной плотности амплитуд воздействия, как амплитудно-частотная характеристика цепи влияет на вид спектральной плотности амплитуд реакции и насколько исказилась форма видеоимпульса при прохождении его через заданную цепь.
В задачах 4.3.1–4.3.25 найдите спектральную плотность амплитуд реакции цепи, заданной в задачах 3.1.1–3.1.25 на видеоимпульс напряжения или тока прямоугольной формы (рис. 3.2) для двух значений длительности импульса tи.
Оцените, как длительность импульса влияет на вид спектральной плотности амплитуд воздействия, как амплитудно-частотная характеристика цепи влияет на вид спектральной плотности амплитуд реакции и насколько исказилась форма видеоимпульса при прохождении его через заданную цепь.
1. Возьмите выражение для амплитудно-частотной характеристики |H(jw)| цепи из задач 4.2.1–4.2.25 и рассчитайте величину граничной частоты wгр полосы пропускания.
2. Запишите выражение спектральной плотности амплитуд воздействия
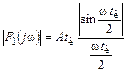 , при w ® 0 |F1(0)| = Atи,
, при w ® 0 |F1(0)| = Atи,
где для видеоимпульса напряжения: A = U0, для видеоимпульса тока: A = I0, и рассчитайте значения двух частот, на которых спектральная плотность амплитуд видеоимпульса с длительностью tи = 2t равна нулю: 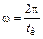 и
и 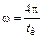 .
.
3. Постройте примерные графики АЧХ цепи и спектральных плотностей амплитуд воздействия и реакции с учетом рассчитанных значений частот в пп. 1 и 2. Возьмите одинаковый масштаб по частоте для всех трех графиков.
4. Оцените, как изменилась спектральная плотность амплитуд воздействия и насколько исказилась форма импульса при прохождении его через цепь (см. задачи 3.2.1–3.2.25).
5. Выполните пп. 2 и 3 при условии, что изменилась длительность импульса:
для нечетных вариантов возьмите 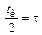 ,
,
для четных вариантов – 2tи = 4t.
6. Проанализируйте, как изменение длительности импульса отразилось на графиках спектральных плотностей амплитуд воздействия и реакции и на форме видеоимпульса при прохождении его через заданную цепь.
Контрольные вопросы
1. Какие колебания имеют дискретный (линейчатый) спектр?
2. Что называют спектром амплитуд и спектром фаз колебания?
3. Как рассчитывается первая (основная) гармоника колебания?
4. Как изменяется спектр колебания при изменении его периода?
5. Каков порядок анализа периодических негармонических колебаний в цепи?
6. Чем определяется изменение амплитуд и начальных фаз гармонических составляющих колебания при прохождении его через линейную цепь?
7. Что означает понятие «сплошной» спектр?
8. Что такое спектральная плотность амплитуд?
9. Что понимают под шириной спектра? От чего она зависит?
10. Какими должны быть частотные характеристики цепи, чтобы колебание не исказилось при прохождении через цепь?
5. Длинные линии
с пренебрежимо малыми потерями
[1, c. 362–364; 2, с. 343–344]
В линиях сравнительно малых длин, которые используются в области высоких частот, можно пренебречь рассеянием энергии, т. е. считать R0 = 0 и G0 = 0. Такая линия имеет чисто резистивное волновое сопротивление 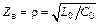 и чисто мнимый коэффициент распространения
и чисто мнимый коэффициент распространения 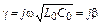 . Коэффициент ослабления a= 0, поэтому амплитуды падающей и отраженной волн не меняются вдоль линии.
. Коэффициент ослабления a= 0, поэтому амплитуды падающей и отраженной волн не меняются вдоль линии.
Комплексные напряжение и ток в любом сечении линии в этом случае определяются по формулам:
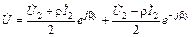 ,
,
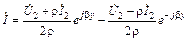 ;
;
или
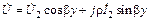 ,
,
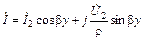 ;
;
или
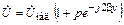 ,
,
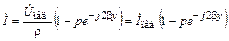 .
.
Коэффициент отражения
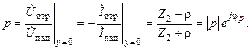
При согласованной нагрузке Z2 =rв линии отсутствует отраженная волна p = 0 иустанавливается режим бегущих волн.
При несогласованной нагрузке Z2 ¹r в линии появляется отраженная волна и устанавливается режим стоячих волн, если ½p½ = 1, либо режим смешанных волн, если ½p½ < 1.
5.1. Режим бегущих волн в линии без потерь
[1, c. 364–365; 2, с. 344–345]
При согласованной нагрузке линии, когда Z2=r и p = 0, отраженная волна в линии отсутствует, т. е. 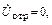 İотр=0.
İотр=0.
Напряжение и ток в любом сечении линии в этом режиме равны напряжению и току падающей волны:
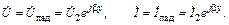
Действующие значения напряжения и тока вдоль всей линии одинаковы: 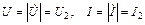 , входное сопротивление в любом сечении равно волновому сопротивлению
, входное сопротивление в любом сечении равно волновому сопротивлению 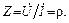
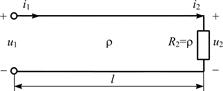 |
| Рис. 5.1 |
5.1.0. Запишите мгновенное значение напряжения u1(t) (рис. 5.1.) на входе согласованно нагруженной линии без потерь длиной l = 10,5 м, если 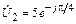 В, l = 20 м. Постройте график распределения действующего значения напряжения U(y) по длине линии.
В, l = 20 м. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.1.1. Рассчитайте входное сопротивление Zвх согласованно нагруженной линии с первичными параметрами L0 = 0,6 мГн/км; С0 = 15 нФ/км; R0 » 0; G0 » 0. Постройте график распределения действующего значения напряжения U(y) по длине линии l = 1,2l, если известен ток в нагрузке I2 = 50 мА.
5.1.2. Запишите мгновенное значение тока i1(t) на входе согласованно нагруженной линии, если u2(t) = 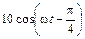 В, и r = 200 Ом. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по длине линии, если l = 1,5 l.
В, и r = 200 Ом. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по длине линии, если l = 1,5 l.
5.1.3. Запишите мгновенное значение тока i2(t) в согласованной нагрузке линии R2 = 100 Ом, если напряжение на ее входе 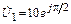 В, l = 15 м, l = 20 м. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по длине линии.
В, l = 15 м, l = 20 м. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по длине линии.
5.1.4. Рассчитайте входное сопротивление Zвх и значение комплексной передаточной функции 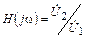 согласованно нагруженной линии длиной l = 500 м, имеющей на частоте w = 8×103 с–1 первичные параметры L0 = 0,4 мкГн/км; С0 = 10 пФ/км; R0 » 0; G0 » 0. Чему равны значения АЧХ и ФЧХ линии на этой частоте?
согласованно нагруженной линии длиной l = 500 м, имеющей на частоте w = 8×103 с–1 первичные параметры L0 = 0,4 мкГн/км; С0 = 10 пФ/км; R0 » 0; G0 » 0. Чему равны значения АЧХ и ФЧХ линии на этой частоте?
5.1.5. Запишите мгновенное значение напряжения u2(t) и рассчитайте средние мощности P1 на входе и P2 в согласованной нагрузке линии длиной l = 1,4l, имеющей первичные параметры L0 = 0,4 мкГн/км; С0 = 10 пФ/км; R0 » 0; G0 » 0, если известно комплексное напряжение на входе линии 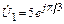 В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.1.6. Запишите мгновенное значение напряжения u2(t) на согласованной нагрузке линии длиной l = 2 м, если известны напряжение на входе линии u1(t) = 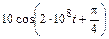 В и фазовая скорость vф = 2×108 м/с. Постройте график распределения действующего значения напряжения U(y) по длине линии.
В и фазовая скорость vф = 2×108 м/с. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.1.7. Запишите мгновенное значение тока i1(t) на входе линии длиной l = 15 м, если напряжение на согласованной нагрузке линии R2 = 400 Ом равно u2(t) = 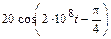 В и фазовая скорость vф = 108 м/с. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
В и фазовая скорость vф = 108 м/с. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
5.1.8. Рассчитайте, на какое сопротивление R2 следует нагрузить линию с первичными параметрами L0 = 0,6 мГн/км; С0 = 15 нФ/км; R0 » 0; G0 » 0, чтобы в ней установился режим бегущих волн? Запишите мгновенное значение тока i1(t) на входе линии длиной l = 1,2 l, если известно напряжение на нагрузке 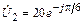 . Постройте график распределения действующего значения тока I(y) по длине линии.
. Постройте график распределения действующего значения тока I(y) по длине линии.
5.1.9. Рассчитайте действующие значения напряжений падающей и отраженной волн в согласованно нагруженной линии с волновым сопротивлением r = 300 Ом и комплексный ток 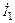 на входе линии, если комплексный ток на нагрузке
на входе линии, если комплексный ток на нагрузке 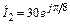 мА. Постройте график распределения действующего значения тока I(y) по длине линии l = 1,25 l.
мА. Постройте график распределения действующего значения тока I(y) по длине линии l = 1,25 l.
5.1.10. Запишите мгновенное значение тока i1(t) на входе согласованно нагруженной линии длиной l = 1,25 м, если ток в нагрузке меняется по закону i2(t) = 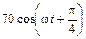 мА и длина волны в линии l = 10 м. Постройте график распределения действующего значения тока I(y) по длине линии.
мА и длина волны в линии l = 10 м. Постройте график распределения действующего значения тока I(y) по длине линии.
5.1.11. Запишите мгновенное значение напряжения u2(t) на согласованной нагрузке линии R2 = r = 500 Ом, если ток на входе линии меняется по закону i0(t) = 40 cos wt мА и длина линии l = 2,1l. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
5.1.12. Запишите мгновенное значение напряжения u1(t) на входе согласованно нагруженной линии, если ток в нагрузке меняется по закону i2(t) = 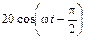 мА, r = 150 Ом, l = 1,25l. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии
мА, r = 150 Ом, l = 1,25l. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии
5.1.13. Рассчитайте действующие значения токов падающей Iпад и отраженной Iотр волн в согласованно нагруженной линии с волновым сопротивлением r = 500 Ом и запишите мгновенное значение тока i1(t) на входе, если комплексное напряжение на нагрузке 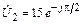 В. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,3 l.
В. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,3 l.
5.1.14. Запишите мгновенное значение тока i1(t) на входе согласованно нагруженной линии с первичными параметрами L0 = 0,5 мГн/км; С0 = 50 нФ/км; R0 » 0; G0 » 0, если ко входу линии приложено напряжение u1(t) = 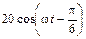 В. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,5 l.
В. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,5 l.
5.1.15. Запишите мгновенное значение напряжения u2(t) и рассчитайте мощность P2 в согласованной нагрузке линии R2 = 500 Ом, если ток на ее входе меняется по закону i1(t) = 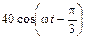 мА. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по длине линии l = 1,75l.
мА. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по длине линии l = 1,75l.
5.1.16. Рассчитайте действующие значения напряжений падающей Uпад и отраженной Uотр волн в линии, нагруженной на сопротивление R2 = r = 300 Ом, если известны комплексный ток на входе линии 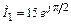 мА, l = 50 м, l = 40 м. Запишите мгновенное значение напряжения u2(t) на нагрузке линии, и постройте график распределения действующего значения тока I(y) по длине линии
мА, l = 50 м, l = 40 м. Запишите мгновенное значение напряжения u2(t) на нагрузке линии, и постройте график распределения действующего значения тока I(y) по длине линии
5.1.17. Запишите мгновенное значение тока i1(t) на входе согласованно нагруженной линии, если на нагрузке R2 = 200 Ом известно напряжение u2(t) = 20 cos wt В. Рассчитайте входное сопротивление линии, и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,5 l.
5.1.18. Запишите мгновенное значение напряжения u2(t) на согласованной нагрузке линии длиной l = 30 м с первичными параметрами L0 = 0,5 мкГн/км; С0 = 50 пФ/км; R0 » 0; G0 » 0, если ток на входе линии равен i1(t) = 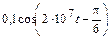 А и длина волны в линии l = 24 м. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
А и длина волны в линии l = 24 м. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
5.1.19. Запишите мгновенные значения тока i1(t) и напряжения u1(t) на входе линии, нагруженной на R2 = r = 500 Ом, если комплексный ток в нагрузке 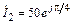 мА. Постройте график распределения действующего значения напряжения U(y) по длине линии l = 1,75 l.
мА. Постройте график распределения действующего значения напряжения U(y) по длине линии l = 1,75 l.
5.1.20. Запишите мгновенное значение тока i1(t) на входе согласованно нагруженной линии, если ток в нагрузке меняется по закону 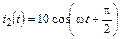 мА, r = 250 Ом, l = 2,4l. Рассчитайте входное сопротивление Zвх и среднюю мощность P1 на входе этой линии. Постройте график распределения действующего значения тока I(y) по длине линии.
мА, r = 250 Ом, l = 2,4l. Рассчитайте входное сопротивление Zвх и среднюю мощность P1 на входе этой линии. Постройте график распределения действующего значения тока I(y) по длине линии.
5.1.21. Запишите мгновенное значение напряжения u1(t) на входе согласованно нагруженной линии с первичными параметрами L0 = 0,9 мГн/км; С0 = 10 нФ/км; R0 » 0; G0 » 0, если комплексный ток в нагрузке линии равен 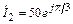 мА. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,5 l.
мА. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,5 l.
5.1.22. Запишите мгновенное значение тока i1(t) на входе линии, нагруженной на R2 = r = 500 Ом, если комплексное напряжение на нагрузке 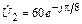 В. Рассчитайте входное сопротивление Zвх и среднюю мощность P1 на входе этой линии. Постройте график распределения действующего значения тока I(y) по длине линии l = 1,25 l.
В. Рассчитайте входное сопротивление Zвх и среднюю мощность P1 на входе этой линии. Постройте график распределения действующего значения тока I(y) по длине линии l = 1,25 l.
5.1.23. Запишите мгновенные значения тока i2(t) и напряжения u2(t) на согласованной нагрузке линии длиной l = 2,3l, если комплексное напряжение на входе линии 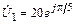 В и волновое сопротивление r = 250 Ом. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
В и волновое сопротивление r = 250 Ом. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
5.1.24. Рассчитайте входное сопротивление Zвх согласованно нагруженной линии с первичными параметрами L0 = 0,8 мкГн/км; С0 = 20 пФ/км; R0 » 0; G0 » 0. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,5 l, если известен ток на входе линии I1 = 30 мА.
5.1.25. Запишите мгновенные значения тока i2(t) и напряжения u2(t) на согласованной нагрузке линии R2 = 10 Ом, если ко входу линии приложено напряжение u1(t) = 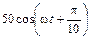 В. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,4l.
В. Постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии l = 1,4l.
5.2. Режим стоячих волн в линии без потерь
[1, c. 365–367; 2, с. 345–350]
В том случае, когда концы линии разомкнуты (режим холостого хода при Z2=¥) или замкнуты накоротко (режим короткого замыкания при Z2 = 0), или когда нагрузка чисто реактивная (Z2 = ± jx2), энергия нагрузкой не рассеивается и амплитуда отраженной волны равна амплитуде падающей волны, т. е. ½p½ = 1. При этом в линии устанавливаются так называемые «стоячие волны».
Режим стоячих волн характерен тем, что в тех сечениях лини, где фазы напряжения (тока) падающей и отраженной волн одинаковы, амплитуда суммарного напряжения (тока) максимальна и равна удвоенной амплитуде напряжения (тока) падающей волны. В тех сечениях, где фазы напряжения (тока) падающей и отраженной волн отличаются на p,амплитуда суммарного напряжения (тока) равна нулю. Первые точки называются пучностями напряжения (тока), вторые – узлами. Узлы и пучности отстоят друг от друга на l/4,причем узлы напряжения совпадают с пучностями тока и наоборот.
Входное сопротивление в любом сечении такой линии чисто реактивно, равно нулю в узлах напряжения и обращается в бесконечность в пучностях напряжения.
Входное сопротивление линии рассчитывается по формулам:
для режима короткого замыкания – Zвх = jr tg bl;
для режима холостого хода – Zвх = –jr ctg bl;
для нагрузки Z2 = jwL – Zвх = jr tg b(l + 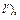 где
где 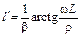 ;
;
для нагрузки 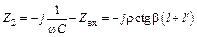 , где
, где 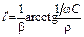 .
.
5.2.0. Найдите ближайшее к концу линии сечение (y0) (рис. 5.2), где напряжение имеет максимальную амплитуду. Постройте график распределения действующего значения напряжения U(y) по длине линии l = 1,5l, если линия нагружена на индуктивность с сопротивлением Z2 = jr и амплитуда падающей волны в линии Um пад = 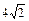 В.
В.
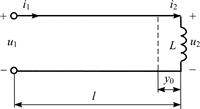 | 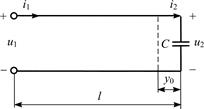 |
| Рис. 5.2 | Рис. 5.3 |
5.2.1. Найдите ближайшее к концу линии сечение (y0) (рис. 5.3), где
ток имеет максимальную амплитуду. Постройте график распределения действующих значений напряжения U(y) и тока I(y) по длине линии l = 1,5l, если линия нагружена на емкость с сопротивлением Z2 = –jr, r = 100 Ом и амплитуда падающей волны в линии Um пад = 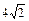 В.
В.
5.2.2. Найдите мгновенные значения тока i1(t) и напряжения u1(t) на входе короткозамкнутой линии (рис. 5.4), если 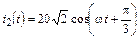 мА и r = 200 Ом. Рассчитайте входное сопротивление линии и постройте график распределения действующего значения тока I(y) по длине линии l = 1,125l.
мА и r = 200 Ом. Рассчитайте входное сопротивление линии и постройте график распределения действующего значения тока I(y) по длине линии l = 1,125l.
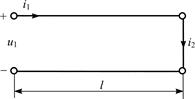 |  |
| Рис. 5.4 | Рис. 5.5 |
5.2.3. Найдите комплексные ток 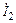 и напряжение
и напряжение 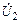 в конце разомкнутой линии (рис. 5.5) длиной l = 1,625l, если известно напряжение в начале линии
в конце разомкнутой линии (рис. 5.5) длиной l = 1,625l, если известно напряжение в начале линии 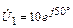 В и r = 100 Ом. Рассчитайте входное сопротивление Zвх линии, найдите комплексный ток в начале линии
В и r = 100 Ом. Рассчитайте входное сопротивление Zвх линии, найдите комплексный ток в начале линии 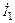 и постройте график распределения действующего значения напряжения U(y) по длине линии.
и постройте график распределения действующего значения напряжения U(y) по длине линии.
5.2.4. Рассчитайте входное сопротивление Zвх короткозамкнутой линии (рис. 5.4) длиной l = 1,625l с волновым сопротивлением r = 150 Ом. Найдите комплексное напряжение 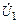 на входе и комплексный ток
на входе и комплексный ток 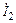 в конце линии, если известен ток в начале линии
в конце линии, если известен ток в начале линии 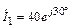 мА. Постройте графики изменения сопротивления Z(y)/j и действующего значения напряжения U(y) по длине линии.
мА. Постройте графики изменения сопротивления Z(y)/j и действующего значения напряжения U(y) по длине линии.
5.2.5. Рассчитайте входное сопротивление Zвх разомкнутой на конце линии (рис. 5.5) длиной l = 1,125l с волновым сопротивлением r = 200 Ом. Найдите мгновенные значения тока i1(t) и напряжения u1(t) на входе линии, если известно напряжение в конце линии 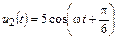 В. Постройте графики изменения сопротивления Z(y)/j и действующего значения тока I(y) по длине линии.
В. Постройте графики изменения сопротивления Z(y)/j и действующего значения тока I(y) по длине линии.
5.2.6. Найдите комплексные ток 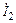 и напряжение
и напряжение 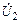 в конце короткозамкнутой линии (рис. 5.4) длиной l = 2,125l, если известно напряжение в начале линии
в конце короткозамкнутой линии (рис. 5.4) длиной l = 2,125l, если известно напряжение в начале линии 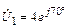 и r = 500 Ом. Рассчитайте входное сопротивление Zвх линии, найдите комплексный ток в начале линии
и r = 500 Ом. Рассчитайте входное сопротивление Zвх линии, найдите комплексный ток в начале линии 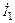 и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
5.2.7. Найдите мгновенные значения напряжений на входе u1(t) и в конце u2(t) разомкнутой линии (рис. 5.5), если 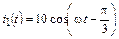 мА и r = 500 Ом. Рассчитайте входное сопротивление линии Zвх и постройте графики изменения сопротивления Z(y)/j и действующего значения напряжения U(y) по линии длиной l = 2,125l.
мА и r = 500 Ом. Рассчитайте входное сопротивление линии Zвх и постройте графики изменения сопротивления Z(y)/j и действующего значения напряжения U(y) по линии длиной l = 2,125l.
5.2.8. Запишите мгновенные значения токов падающей iпад2(t) и отраженной iотр2(t) волн в конце короткозамкнутой линии (рис. 5.4), если 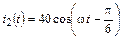 мА. Рассчитайте входное сопротивление Zвх линии и найдите мгновенные значения тока i1(t) и напряжения u1(t) в начале линии длиной l = 3,125l с волновым сопротивлением r = 100 Ом. Постройте график распределения действующего значения тока I(y) по длине линии.
мА. Рассчитайте входное сопротивление Zвх линии и найдите мгновенные значения тока i1(t) и напряжения u1(t) в начале линии длиной l = 3,125l с волновым сопротивлением r = 100 Ом. Постройте график распределения действующего значения тока I(y) по длине линии.
5.2.9. Запишите мгновенные значения напряжений падающей uпад2(t) и отраженной uотр2(t) волн в конце разомкнутой линии (рис. 5.5), если 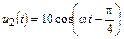 В. Рассчитайте входное сопротивление Zвх линии и найдите мгновенные значения тока i1(t) и напряжения u1(t) в начале линии длиной l = 3,125l с волновым сопротивлением r = 200 Ом. Постройте график распределения действующего значения напряжения U(y) по длине линии.
В. Рассчитайте входное сопротивление Zвх линии и найдите мгновенные значения тока i1(t) и напряжения u1(t) в начале линии длиной l = 3,125l с волновым сопротивлением r = 200 Ом. Постройте график распределения действующего значения напряжения U(y) по длине линии.
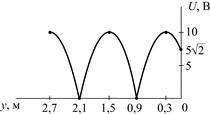 |
| Рис. 5.6 |
5.2.10. Рассчитайте сопротивление Z2, на которое нагружена линия с волновым сопротивлением r = 100 Ом, если известно распределение напряжения по линии (рис. 5.6). Рассчитайте действующие значения тока I2 в нагрузке и тока Imax в пучностях и постройте график распределения действующего значения тока I(y) по длине линии.
5.2.11. Рассчитайте значение коэффициента отражения p в конце линии с волновым сопротивлением r = 150 Ом, если известно распределение напряжения по линии (рис. 5.6). Запишите мгновенные значения напряжений падающей uпад2(t) и отраженной uотр2(t) волн в конце линии, если начальная фаза напряжения u2(t) составляет j = 70°.
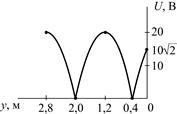 |
| Рис. 5.7 |
5.2.12. Рассчитайте сопротивление Z2, на которое нагружена линия с волновым сопротивлением r = 200 Ом, если известно распределение напряжения по линии (рис. 5.7). Рассчитайте действующие значения тока I2 в нагрузке и тока Imax в пучностях и постройте график распределения действующего значения тока I(y) по длине линии.
5.2.13. Рассчитайте значение коэффициента отражения p в конце линии с волновым сопротивлением r = 250 Ом, если известно распределение напряжения по линии (рис. 5.7). Запишите мгновенные значения напряжений падающей uпад2(t) и отраженной uотр2(t) волн в конце линии, если начальная фаза напряжения u2(t) составляет j = 15°.
5.2.14. Рассчитайте сопротивление Z2, на которое нагружена линия длиной l = 1,25l с волновым сопротивлением r = 300 Ом, и найдите комплексные напряжения отраженной 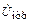 волны,
волны, 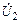 в конце и
в конце и 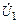 в начале линии, если известны комплексное напряжение
в начале линии, если известны комплексное напряжение 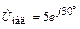 В и коэффициент отражения p = j. Постройте график распределения действующего значения напряжения U(y) по длине линии.
В и коэффициент отражения p = j. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.2.15. Рассчитайте сопротивление Z2, на которое нагружена линия длиной l = 1,5l с волновым сопротивлением r = 400 Ом, и найдите комплексные токи отраженной 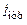 волны,
волны, 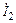 в конце и
в конце и 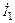 в начале линии, если известны комплексный ток
в начале линии, если известны комплексный ток 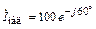 мА и коэффициент отражения p = –j. Постройте график распределения действующего значения тока I(y) по длине линии.
мА и коэффициент отражения p = –j. Постройте график распределения действующего значения тока I(y) по длине линии.
 |
| Рис. 5.8 |
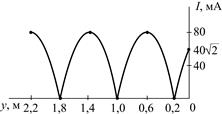
5.2.16. Рассчитайте сопротивление Z2, на которое нагружена линия с волновым сопротивлением r = 125 Ом, если известно распределение тока по линии (рис. 5.8). Рассчитайте действующие значения напряжения U2 на нагрузке и напряжения Umax в пучностях и постройте график изменения действующего значения напряжения U(y) по длине линии.
5.2.17. Рассчитайте значение коэффициента отражения p в конце линии с волновым сопротивлением r = 350 Ом, если известно распределение тока по линии (рис. 5.8). Запишите мгновенные значения токов падающей iпад2(t) и отраженной iотр2(t) волн в конце линии, если начальная фаза тока i2(t) составляет j = –60°.
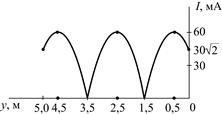 |
| Рис. 5.9 |
5.2.18. Рассчитайте сопротивление Z2, на которое нагружена линия с волновым сопротивлением r = 300 Ом, если известно распределение тока по линии (рис. 5.9). Рассчитайте действующие значения напряжения U2 на нагрузке и напряжения Umax в пучностях и постройте график распределения действующего значения напряжения U(y) по длине линии.
5.2.19. Рассчитайте значение коэффициента отражения p в конце линии с волновым сопротивлением r = 400 Ом, если известно распределение тока по линии (рис. 5.9). Запишите мгновенные значения токов падающей iпад2(t) и отраженной iотр2(t) волн в конце линии, если начальная фаза тока i2(t) составляет j = 55°.
5.2.20. Найдите мгновенные значения напряжения u1(t) на входе и тока i2(t) на выходе короткозамкнутой линии (рис. 5.4), если 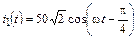 мА и r = 250 Ом. Рассчитайте входное сопротивление Zвх линии и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по линии длиной l = 1,375l.
мА и r = 250 Ом. Рассчитайте входное сопротивление Zвх линии и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по линии длиной l = 1,375l.
5.2.21. Рассчитайте входное сопротивление Zвх короткозамкнутой линии (рис. 5.4) длиной l = 1,125l с волновым сопротивлением r = 100 Ом. Найдите мгновенные значения токов i1(t) на входе и i2(t) на выходе линии и запишите мгновенные значения токов падающей iпад2(t) и отраженной iотр2(t) волн в конце линии, если 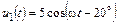 В. Постройте график распределения действующего значения тока I(y) по длине линии.
В. Постройте график распределения действующего значения тока I(y) по длине линии.
5.2.22. Рассчитайте входное сопротивление Zвх разомкнутой на конце линии (рис. 5.5) длиной l = 1,625l с волновым сопротивлением r = 400 Ом. Найдите мгновенные значения тока i1(t) на входе и напряжения u2(t) на выходе линии и запишите мгновенные значения напряжений падающей uпад2(t) и отраженной uотр2(t) волн в конце линии, если 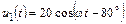 В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.2.23. Найдите комплексные ток 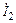 и напряжение
и напряжение 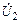 в конце разомкнутой линии (рис. 5.5) длиной l = 1,375l, если известен комплексный ток в начале линии
в конце разомкнутой линии (рис. 5.5) длиной l = 1,375l, если известен комплексный ток в начале линии 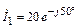 и r = 150 Ом. Рассчитайте входное сопротивление Zвх линии, найдите комплексное напряжение в начале линии
и r = 150 Ом. Рассчитайте входное сопротивление Zвх линии, найдите комплексное напряжение в начале линии 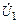 и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
и постройте графики распределения действующих значений тока I(y) и напряжения U(y) по длине линии.
5.2.24. Рассчитайте входное сопротивление Zвх линии длиной l = 1,25l с волновым сопротивлением r = 200 Ом, если линия нагружена на емкость с сопротивлением Z2 = –j200 Ом (рис. 5.3). Найдите комплексный ток 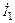 на входе и комплексные напряжения
на входе и комплексные напряжения 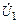 на входе и
на входе и 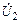 на выходе линии, если комплексный ток на выходе линии
на выходе линии, если комплексный ток на выходе линии 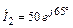 мА. Постройте график распределения действующего значения напряжения U(y) по длине линии.
мА. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.2.25. Рассчитайте входное сопротивление Zвх линии длиной l = 1,5l с волновым сопротивлением r = 500 Ом, если линия нагружена на индуктивность с сопротивлением Z2 = j500 Ом (рис. 5.2). Найдите комплексное напряжение 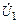 на входе и комплексные токи
на входе и комплексные токи 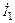 на входе и
на входе и 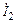 на выходе линии, если комплексное напряжение на выходе линии
на выходе линии, если комплексное напряжение на выходе линии 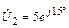 В. Постройте график распределения действующего значения тока I(y) по длине линии.
В. Постройте график распределения действующего значения тока I(y) по длине линии.
5.3. Режим смешанных волн в линии без потерь
[1, с. 368–369; 2, с. 350–352]
В том случае, когда нагрузка линии резистивная, не равная волновому сопротивлению (Z2 = R2 ¹ r), или комплексная (Z2 = R2 ± jx2),часть энергии падающей волны рассеивается нагрузкой, а остальная часть отражается. Амплитуда отраженной волны в этом случае меньше амплитуды падающей волны, т. е. |р| < 1. B линии устанавливается режим смешанных волн, характерный тем, что напряжение (ток) можно представить как сумму напряжений (токов) бегущей и стоячей волн, что приводит к появлению сечений в которых напряжение (ток) принимают максимальные либо минимальные значения.
В сечениях, где амплитуда напряжения (тока) равна разности амплитуд падающей и отраженной волн, ее значение минимально, а в сечении, где она равна сумме амплитуд падающей и отраженной волн – максимально:
Umin = Uпад – Uотр = Uпад(1 – ïpï),
Umax = Uпад + Uотр = Uпад(1 + ïpï).
Входное сопротивление линии в режиме смешанных волн в общем случае комплексно и только в точках экстремумов напряжения (тока) имеет резистивный характер (Z = Rpeз). Такие сечения называются резонансными. Сопротивление в резонансном сечении ypeз максимально (Rpeз = Rmax), если амплитуда напряжения в нем максимальна (U = Umax), а амплитуда тока минимальна (I = Imin) и минимально (Rpeз = Rmin),если U = Umin, а I = Imax.
Резонансные сопротивления и соответствующие сечения могут быть определены по формулам:
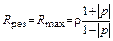 при
при 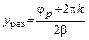 ; k = 0, 1, …,
; k = 0, 1, …,
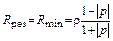 при
при 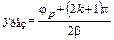 ; k = 0, 1, … ,
; k = 0, 1, … ,
здесь ½p½ – модуль коэффициента отражения; jр – его аргумент.
Отношение минимальной и максимальной амплитуд напряжения (тока) называют коэффициентом бегущей волны:
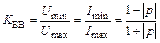 ,
,
величина KБВ изменяется в пределах 0 £ KБВ £ 1.
В режиме бегущих волн KБВ = 1, стоячих волн KБВ = 0, а смешанных – рассчитывается по одной из формул
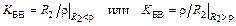 ,
,
так как по определению KБВ < 1.
Входное сопротивление линии
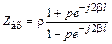 .
.
 |
| Рис. 5.10 |
5.3.0. Рассчитайте действующее значение напряжения U2 в конце линии, нагруженной на комплексное сопротивление Z2 = R2 – 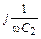 (рис. 5.10), если известны напряжение падающей волны Uпад = 5 В и коэффициент отражения
(рис. 5.10), если известны напряжение падающей волны Uпад = 5 В и коэффициент отражения 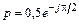 . Постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,5l.
. Постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,5l.
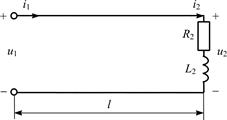 |
| Рис. 5.11 |
5.3.1. Рассчитайте действующее значение напряжения U2 в конце линии, нагруженной на комплексное сопротивление Z2 = R2 + jwL2 (рис. 5.11), если известны напряжение отраженной волны Uотр = 5 В и коэффициент отражения 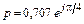 . Постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,5l.
. Постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,5l.
5.3.2. Рассчитайте действующее значение напряжения U1 в начале линии, нагруженной на резистивное сопротивление R2 (рис. 5.12), если R2 = 300 Ом, r = 200 Ом, U2 = 6 В. Рассчитайте входное сопротивление Zвх, значения коэффициента отражения p и коэффициента бегущей волны KБВ, и постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,25l.
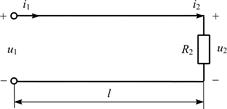 |
| Рис. 5.12 |
5.3.3. Рассчитайте, при каком R2 < r (рис. 5.12) в линии с волновым сопротивлением r = 200 Ом, коэффициент бегущей волны составит KБВ = 0,5. Рассчитайте действующие значения напряжений U1 в начале и U2 в конце линии, если напряжение падающей волны Uпад = 9 В, и постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,75l.
5.3.4. Рассчитайте действующие значения напряжения U1 в начале и U2 в конце линии (рис. 5.12), если R2 = 200 Ом, r = 300 Ом, Uотр = 5 В. Рассчитайте входное сопротивление Zвх, значения коэффициента отражения p и коэффициента бегущей волны KБВ, и постройте график распределения действующего значения напряжения U(y) по линии длиной l =0,75l.
5.3.5. Рассчитайте входное сопротивление Zвх, линии (рис. 5.12) и действующие значения напряжения U1 в начале и токов I1 в начале и I2 в конце линии, если R2 = 300 Ом, r = 100 Ом, U2 = 12 В. Постройте графики распределения действующих значений напряжения U(y) и тока I(y) по линии длиной l =1,75l.
5.3.6. Рассчитайте, при каком R2 > r (рис. 5.12) в линии с волновым сопротивлением r = 400 Ом, коэффициент бегущей волны составит KБВ = 0,4. Рассчитайте действующие значения напряжений U1 в начале и U2 в конце линии, если напряжение отраженной волны Uотр = 12 В, и постройте график распределения действующего значения напряжения U(y) по линии длиной l =1,25l.
5.3.7. Постройте график распределения действующего значения напряжения U(y) по длине линии l =1,25l, если известны коэффициент отражения p = –0,5, ток отраженной волны Iотр = 20 мА и r = 150 Ом.
5.3.8. Постройте график распределения действующего значения тока I(y) по длине линии l =1,25l, если R2 = 200 Ом (рис. 5.12), r = 500 Ом, U2 = 10 В. Рассчитайте токи падающей Iпад и отраженной Iотр волн.
5.3.9. Рассчитайте действующее значение напряжения U1 на входе линии длиной l =1,125l, если известны коэффициент отражения 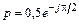 и максимальное напряжение в линии Umax = 15 В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
и максимальное напряжение в линии Umax = 15 В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.3.10. Рассчитайте действующее значение напряжения U1 на входе линии длиной l =0,875l, если известны коэффициент отражения 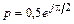 и напряжение отраженной волны Uотр = 8 В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
и напряжение отраженной волны Uотр = 8 В. Постройте график распределения действующего значения напряжения U(y) по длине линии.
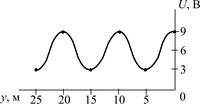 |
| Рис. 5.13 |
5.3.11. Найдите входное сопротивление Zвх, сопротивление нагрузки Z2 и действующие значения напряжений падающей Uпад и отраженной Uотр волн в линии с волновым сопротивлением r = 150 Ом, если известно распределение напряжения U(y) по длине линии (рис. 5.13). Постройте график распределения действующего значения тока I(y) по длине линии.
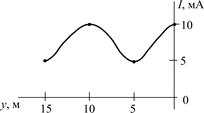 |
| Рис. 5.14 |
5.3.12. Найдите входное сопротивление Zвх, волновое сопротивление r и действующие значения токов падающей Iпад и отраженной Iотр волн в линии, нагруженной на сопротивление R2 = 200 Ом, если известно распределение тока I(y) по длине линии (рис. 5.14). Постройте график распределения действующего значения напряжения U(y) по длине линии.
5.3.13. Рассчитайте действующие значения напряжения U1 в начале и U2 в конце линии с волновым сопротивлением r = 200 Ом, нагруженной на сопротивление Z2 = 200 – j400 Ом (рис. 5.10), если известно напряжение падающей волны Uпад = 10 В. Постройте график распределения действующего значения напряжения U(y) по линии длиной l =l.
5.3.14. Рассчитайте действующие значения напряжения U1 в начале и U2 в конце линии с волновым сопротивлением r = 300
