Тригонометрические функции
МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ
Действия над многочленами
 – (a + b – c)x=–ax – bx + cx; (a + b – c)(x + y)=ax + ay + bx + by – cx – cy
– (a + b – c)x=–ax – bx + cx; (a + b – c)(x + y)=ax + ay + bx + by – cx – cy
Дроби
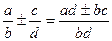 ;
; 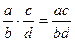 ;
; 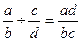 ;
; 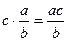 ;
; 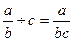 ;
; 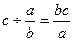
Формулы сокращённого умножения
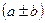 2= a2 ± 2ab + b2 (a ± b)3 = a3 ± 3ab2 + 3a2b ± b3 a2 – b2 = (a–b)(a+b)
2= a2 ± 2ab + b2 (a ± b)3 = a3 ± 3ab2 + 3a2b ± b3 a2 – b2 = (a–b)(a+b)
a3 ± b3 = (a ± b)(a2 ± ab + b2)
Степени
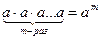
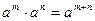
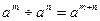
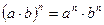
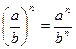
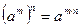
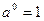
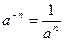
Корни
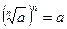
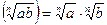
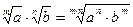
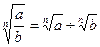
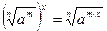
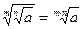
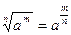
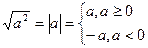
Квадратное уравнение
Общего вида: с чётным 2–м коэффициентом
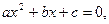
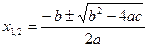
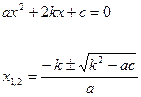
Приведённое разложение трёхчлена на множители
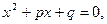
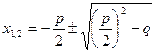
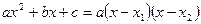
Теорема Виета для приведённого уравнения
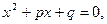
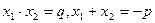
Неравенства второй степени
| D=b2–4ac | a>0 | график | |
| ax2 + bx + c>0 | ax2 + bx + c<0 | ||
| D>0 x1<x2 | x<x1 x>x2 | x1<x<x2 | |
| D=0 x1=x2 | x<x1 x>x1 | нет решений | |
| D<0 корней нет | x  R R | нет решений |
Неравенства с переменной в знаменателе дроби
1. неравенство 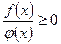 сводиться к системам: 2.неравенство
сводиться к системам: 2.неравенство 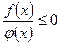 сводится к системам:
сводится к системам:
1) 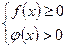 2)
2) 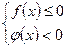 1)
1) 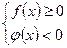 2)
2) 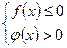
ПРОГРЕССИИ
Арифметическая прогрессия
Общий член 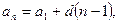 d – разность прогрессии, т.е.
d – разность прогрессии, т.е. 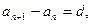 или
или 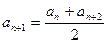
Сумма n – первых членов 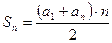 или
или 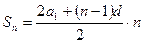
Геометрическая прогрессия
Общий член 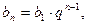 где q – знаменатель прогрессии сумма членов бесконечно
где q – знаменатель прогрессии сумма членов бесконечно
Свойства геометрической прогрессии: 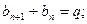
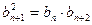 убывающей прогрессии:
убывающей прогрессии:
Сумма n – первых членов 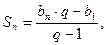 или
или 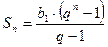
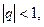
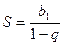
ЛОГАРИФМЫ
Логарифмом числа b по основанию a называется показатель степени c, в которую нужно возвести основание a, чтобы получилось число b. 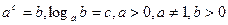
Основное логарифмическое тождество: 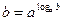
Свойства логарифмов: 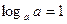 ;
; 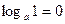 ;
; 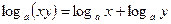 ;
; 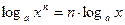 ;
;
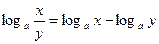 ;
; 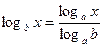 ;
; 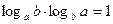 ;
; 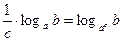 ;
; 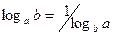
ЗАМЕЧАНИЕ: все числа a,b,x,y– принимают положительные значения, а если они стоят в основании логарифма, то не равны единице.
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
1. уравнения вида: 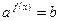 1) при b<0, уравнение решения не имеет
1) при b<0, уравнение решения не имеет
2) при 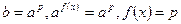
3) при 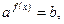 уравнение можно решить логарифмируя по основанию а, получим
уравнение можно решить логарифмируя по основанию а, получим 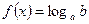
2. уравнения вида: 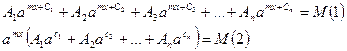 выражение, находящиеся в скобках уравнения (2), является величиной постоянной; обозначим эту величину буквой N, тогда уравнение (2) примет вид
выражение, находящиеся в скобках уравнения (2), является величиной постоянной; обозначим эту величину буквой N, тогда уравнение (2) примет вид 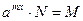 , при N ≠ 0 имеем:
, при N ≠ 0 имеем: 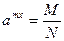
3. уравнение вида: 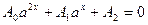 (1) с помощью подстановки
(1) с помощью подстановки 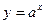 обращается в обычное квадратное уравнение
обращается в обычное квадратное уравнение 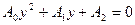 , где y1 и y2 – корни. Далее решение уравнения (1) сводится к решению двух уравнений: 1)
, где y1 и y2 – корни. Далее решение уравнения (1) сводится к решению двух уравнений: 1) 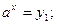 2)
2) 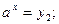
4. уравнение вида: 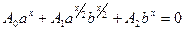 легко привести к виду уравнения (1) из 3.
легко привести к виду уравнения (1) из 3.
разделив это уравнение на 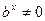 :
: 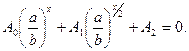 С помощью подстановки
С помощью подстановки 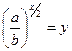 , уравнение принимает вид:
, уравнение принимает вид: 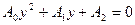 и сводится к решению двух уравнений: 1)
и сводится к решению двух уравнений: 1) 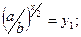 2)
2) 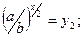
ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
1. 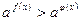 1) при
1) при 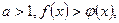
2) при 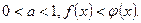
аналогично для неравенства  .
.
2. для неравенства вида 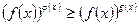 решение сводится к решению систем:
решение сводится к решению систем:
1) 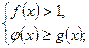 2)
2) 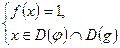 3)
3) 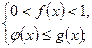 4)
4) 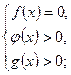
аналогично для неравенства: 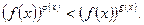
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
1. неравенство вида 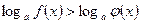 сводится к решению одной из систем:
сводится к решению одной из систем:
1) при a>1 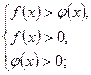 2) при 0<a<1
2) при 0<a<1 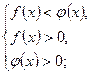 аналогично для неравенства:
аналогично для неравенства: 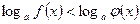
2. неравенство вида 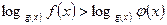 сводиться к решению двух систем:
сводиться к решению двух систем:
1) 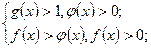 2)
2) 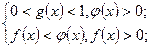 аналогично для неравенства
аналогично для неравенства 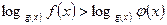
ПРОИЗВОДНАЯ
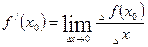 значение производной функции в точке
значение производной функции в точке 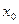 равно угловому коэффициенту касательной к графику функции в этой точке.
равно угловому коэффициенту касательной к графику функции в этой точке. 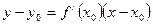 – уравнение касательной к графику функции
– уравнение касательной к графику функции 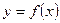 в точке
в точке 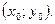
ФОРМУЛЫ ПРОИЗВОДНЫХ ОСНОВНЫХ ФУНКЦИЙ
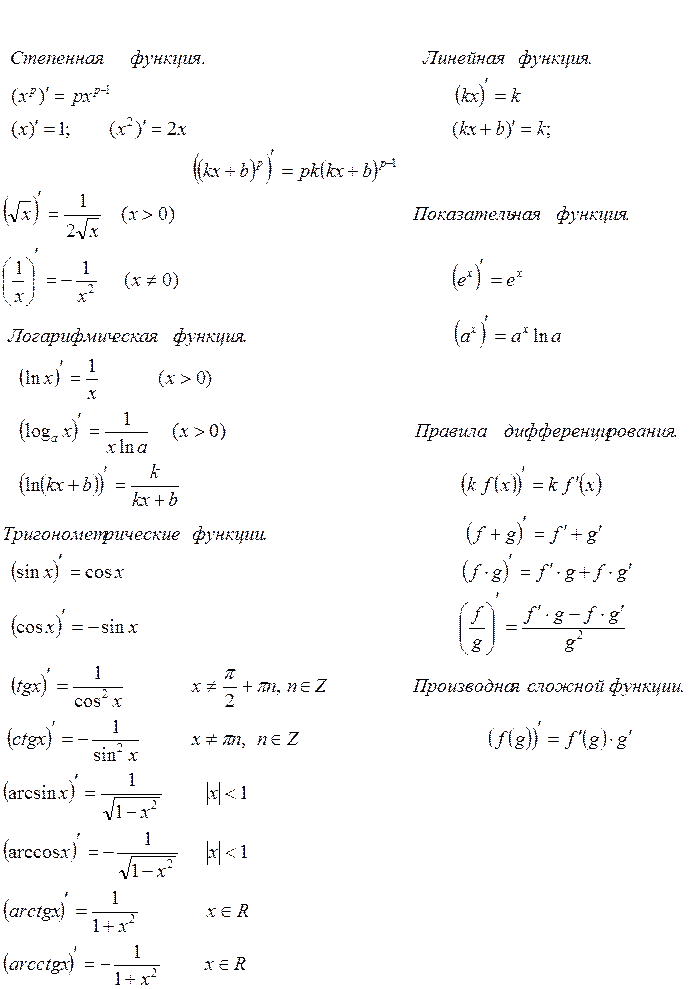
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Определение 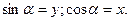 Радианная мера углов 1радиан = 1800/π ≈57,295779520;
Радианная мера углов 1радиан = 1800/π ≈57,295779520;
10 = π/1800 радиан ≈ 0,001745 рад.
