Декартово произведение множеств

Цели занятия: на базе полученных знаний изучить операции над множествами; научиться абстрагировать множества диаграммами Венна и осуществлять операции над ними; изучить понятие «декартово произведение».

Роль и место лекции

В этой лекции мы рассмотрим некоторые способы получения новых множеств из уже имеющихся. Эти способы обычно называются операциями над множествами. Основные свойства этих операций и связи между ними принято называть алгеброй множеств.

Понимание операций над множествами позволит шире взглянуть на уже известные математические операции и обобщить их, т. е. непосредственно подойти к таким понятиям высшей математики как «оператор», «функционал» и др.

Обратите внимание на последний и такое, казалось бы, глобальное известное математическое понятие, как «декартова плоскость», окажется частным случаем. А понимание универсального множества будет важно при изучении бесконечно малых и бесконечно больших величин. Поэтому отмечаем особую важность первых лекций.

Операции над множествами. Диаграммы Венна

Объединение и пересечение

Определение 1.

Объединением (суммой) двух множеств A и B называется множество (его принято обозначать 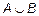), состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств - либо A, либо B

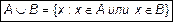. (1)

ПРИМЕР 1.

Рассмотрим множества A = {1, 2, 3, 4}, B = {1,3,5}, C = {5,6}. Тогда согласно введенному определению получаем:

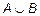= {1, 2, 3, 4, 5}; 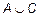= {1, 2, 3, 4, 5, 6}.

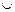Объединение множеств в биологии может определить множество {Род}. Например {Дикая кошка} {Камышовая кошка} 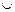… = {Род кошек}.

Аналогично определяется объединение (сумма) n 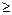2 множеств A₁,A₂, ..., A_n. Объединением этих множеств называется множество, обозначаемое A₁ 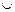A₂ 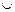... 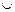A_n, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств.

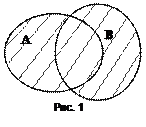Достаточно часто для наглядного изображения этих операций над множествами используют так называемые круги Эйлера (диаграммы Венна). Множества при таком подходе изображают кругами, а результат операции закрашивают или заштриховывают. Результат операции объединения двух множеств представлен на рис. 1.

Определение 2.

Пересечением (произведением) двух множеств A и B называется множество (его принято обозначать 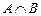), состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств A и B

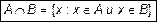. (2)

ПРИМЕР 2.

В рамках введенных в предыдущем примере определений множеств A, B, C мы получаем:

, , .

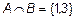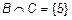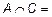
В биологии пересечение множеств может определять среду обитания или произрастания. Например {Редкие растения} 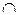{Растения края} = {Заповедник}.

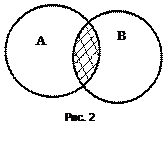
Так же как мы делали раньше, можно определить пересечение (произведение) конечного числа множеств. На кругах Эйлера пересечение множеств представлено на рис. 2.

1. 2. Свойства объединения и пересечения множеств

1. Коммутативности:

; .

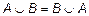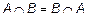2. Ассоциативности:

; .

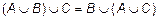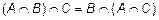Справедливость этих свойств следует из самих определений операций пересечения и объединения множеств, поэтому обычно скобки в таких групповых операциях опускают.

3. Закон взаимной дистрибутивности:

; .

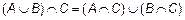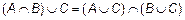Разность множеств

Определение 3.

Разностью двух множеств A и B называется множество (его обычно обозначают A\B или A-B), состоящее из тех и только тех элементов, которые принадлежат множеству A и не принадлежат множеству B .

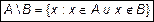. (3)

На кругах Эйлера выражение (3) представлено на рис. 3.

ПРИМЕР 3.

В рамках введенных в примере 1 определений множеств A, B, C справедливы следующие результаты A \ B = {2,4}; B \ C = {1,3}; A \ C = A.

Определение 4.

Симметрической разностью множеств A и B называется множество, обозначаемое через A 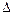B и определяемое следующим образом:

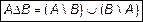. (4)

На кругах Эйлера выражение (4) представлено на рис. 4.

ПРИМЕР 4.

В рамках введенных в примере 1 определений множеств A, B, C справедливы следующие результаты:

;

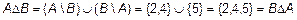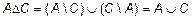, поскольку = .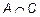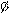