Надежность последовательной системы
К числу важнейших общих зависимостей надежности относятся зависимости надежности систем от надежности элементов.
Рассмотрим надежность наиболее характерной для машиностроения простейшей расчетной модели системы из последовательно соединенных элементов (рисунок 1.6). В этом случае отказ каждого элемента вызывает отказ системы, а отказы элементов принимаются независимыми.
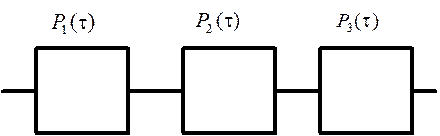
Рисунок 1.6 – Последовательная система
Используем известную теорему умножения вероятностей, согласно которой вероятность произведения, т. е. совместного проявления независимых событий, равна произведению вероятностей этих событий. Следовательно, вероятность безотказной работы системы равна произведению вероятностей безотказной работы отдельных элементов  . Если
. Если 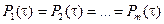 , то
, то 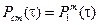 .
.
Поэтому надежность сложных систем получается низкой. Например, если система состоит из 10 элементов с вероятностью безотказной работы 0,9 (как в подшипниках качения), то общая вероятность получается 0,910»0,35.
Обычно вероятность безотказной работы элементов достаточно высокая, поэтому, выразив 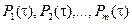 через вероятности отказов и пользуясь теорией приближенных вычислений, получаем
через вероятности отказов и пользуясь теорией приближенных вычислений, получаем


так как произведениями двух малых величин можно пренебречь. При 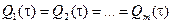 получаем
получаем 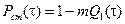 .
.
Пусть в системе из шести последовательных одинаковых элементов 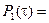 0,99. Тогда
0,99. Тогда 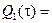 0,01 и
0,01 и  0,94.
0,94.
