Основи кореляційного аналізу

Математичні методи та моделі, які використовуються при проведенні наукових досліджень

При проведенні наукових досліджень проблем, що виникають у різноманітних господарствах залізничного транспорту викликають необхідність застосування кількісних методів, які базуються на прийомах елементарної і вищої математики, а також різних методах теорії ймовірностей і статистики, кореляції та регресії, систем і мереж масового обслуговування, лінійного та динамічного програмування, імітаційного моделювання, сіткових графіків і багато інших.

Використання стохастичних моделей для розв’язання інженерних завдань

Основи кореляційного аналізу

Для розв’язування інженерних завдань і завдань управління часто використовують статистичні звітні данні, або данні спостережень. При цьому убачається, що такі данні є значеннями випадкової величини.

Випадковою величиною є така змінна величина, яка у залежності від випадку приймає різні значення з деякою ймовірністю. Закон розподілу випадкової величини показує частоту її значень у загальній сукупності.

При дослідженні взаємозв’язків між показниками на основі статистичних даних часто між ними спостерігається стохастична залежність. Вона виявляється в тому, що зміна закону розподілу однієї випадкової величини здійснюється під впливом зміни іншої. Взаємозв’язок між величинами може бути повним (функціональним) і неповним (спотвореним іншими факторами).

Розділ математичної статистики, який присвячений вивченню взаємозв’язків між випадковими величинами називається кореляційним аналізом. Основне завдання кореляційного аналізу у встановленні характеру й тісноти зв’язку між результативними (залежними) і факторними (незалежними) показниками (ознаками) у даному явищі або процесі. Кореляційний взаємозв’язок можна виявити лише при масовому зіставлянні фактів.

Характер зв’язку між показниками визначається по кореляційному полю. Якщо у є залежним показником, а х – незалежний, то для кожного випадку з координатами х_і, у_і отримуємо кореляційне поле. За розміщенням точок можна судити про характер зв’язку (рис. 1.1.).

а)

б)

в)

г)

Рис. 4.1.1. Приклади кореляційних полів

а) некорельовані дані; б) пряма кореляція; в) зворотня кореляція; г) фіктивна кореляція (неоднородні дані).

Щільність зв’язку двох змінних може визначається за допомогою лінійного коефіцієнта кореляції (r), який вимірює ступінь лінійної залежності між двома змінними, одна з яких – результативний показник (у), а інша – факторний (х).

У статистиці щільність зв’язку може бути визначена за допомогою різних коефіцієнтів (Фехнера, Пірсона, коефіцієнта асоціації, тощо), частіше використовується лінійний коефіцієнт кореляції, який визначається за формулою:

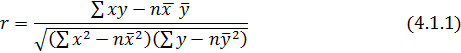
де: 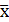- середня арифметична факторного показника;

- середня арифметична результативного показника;

n - число даних у виборці.

Величина коефіцієнта кореляції знаходиться у межах від -1 до +1. Значення r = -1 свідчить про наявність жорсткого детермінованого зворотного пропорційного зв’язку між факторами, r = +1 відповідає жорстко де термі-нованому зв’язку з прямо пропорційною залежністю факторів. Якщо лінійного зв’язку між факторами не спостерігається, то r = 0. Інші значення коефіцієнта кореляції свідчать про наявність стохастичного зв’язку, причому чим ближче до 1, тим щільнішим вважається зв'язок.

Для якісної оцінки міцності зв’язку можна скористатися таблицею Чеддока (табл. 4.1.1).

Табл. 4.1.1

Оцінка міцності зв’язку між результативним і факторним показниками

Значення коефіцієнта	Міцність зв’язку
0,1 – 0,3	Слабка
0,31 – 0,5	Помірна
0,51 – 0,7	Помітна
0,71 – 0,9	Висока
0,91 – 0,99	Дуже висока

Розглянемо приклад визначення міцності зв’язку між результативним та факторним показниками.

Приклад 1. Дослідимо залежність між прибутком від реалізації послуг залізничного підприємства і витратами на рекламу (без обліку інфляції) та оцінимо характер співвідношення між обома змінними за допомогою коефіцієнта кореляції. Результативним показником є отриманий прибуток за послуги (у), а факторним – витрати на рекламу (х). Вихідна інформація із січня по вересень подана у табл. 4.1.2.

Табл. 4.1.2.

Вихідна інформація

Показники	Місяць
Отриманий прибуток (у)
Витрати на рекламу (х)	28,2	26,3	21,2	18,9	18,5	16,2	16,8	25,9	28,9

Визначимо необхідність для подальших розрахунків параметри необхідних похідних величин для розрахунку коефіцієнта кореляції r та зведемо їх у таблицю.

Табл. 4.1.3.

Похідні величини для визначення r

Місяць	n	x	y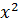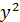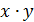
Січень		28,2		795,24		720114,2
Лютий		26,3		691,69		634513,8
Березень		21,2		449,44		435914,4
Квітень		18,9		357,21		352522,7
Травень		18,5		342,25
Червень		16,2		262,44
Липень		16,8		282,24		296066,4
Серпень		25,9		670,81
Вересень		28,9		835,21		748249,9
Всього		200,9		4686,53		439411,5

Знайдемо середньомісячні величини прибутку від надання послуг та витрат на рекламу в період, що аналізується, а також квадрати цих величин:

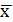= 22,32; =21183,78; 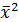= 498,18; 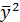= 44875235,09.

Розрахуємо r :

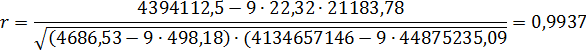
Порівняємо отриману величину з даними таблиці Чеддока.

Отримане значення коефіцієнта кореляції показує, що для підприємства залізничного транспорту зв'язок між витратами на рекламу та прибутком від надання послуг дуже тісний.

При вимірюванні щільності зв’язку при криволінійній формі залежності коефіцієнт кореляції не використовується, а використовується кореляційне відношення.

Нехай є кореляційне поле зв’язку між двома змінними (рис.4.1.2).

Рис.4.1.2 Кореляційне поле зв’язку між двома змінними

Виходячи з рис. 4.1.2. видно, що у результаті спостереження над двомірною випадковою величиною отримано n = 26 пар значень х та у. Отриману вибірку зручно задавати у вигляді кореляційної таблиці (табл. 4.1.4.).

Табл.4.1.4.

Кореляційна таблиця

	х	nyj
0-х1	х1 – х2	х2 – х3	х3 – х4	х4 – х5	х5 – х6	х6 – х7
у	0-у1
у1-у2
у2-у3
у3-у4
у4-у5
у5-у6
nxi

Перед побудовою кореляційної таблиці вибирають розміри розрядів ( 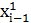, 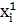), ( , 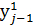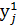) на які розподіляють область емпіричного розподілу кожного показника. Число розрядів для кожного показника належить брати не більше 10, бо при збільшені числа розрядів точність оцінок змінюється не суттєво, а об’єм розрахунків швидко зростає.

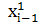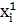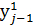У кожну клітинку кореляційної таблиці заноситься частота n_ij – число пар, які задовольняють умовам <x< , <y< .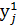

Цим вимірам приписують значення: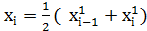

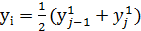(4.1.2.)

У нижню строку таблиці заносять частоти n_xi, а у крайній правий стовбець – частоти n_yj, які визначаються рівністю:

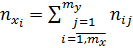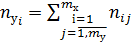, (4.1.3)

де: m_x – число розрядів для показника х;

m_у – число розрядів для показника у.

За даними кореляційної таблиці можуть бути визначені такі статистичні оцінки:

- умовні вибіркові середні

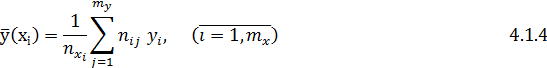
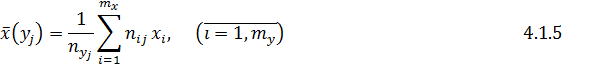
- умовні емпіричні дисперсії

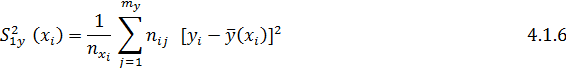
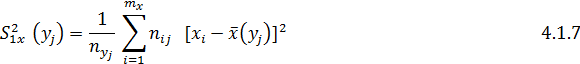
- вибіркові середні

- емпіричні дисперсії

- емпіричні кореляційні відношення

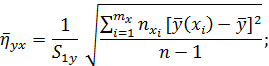
4.1.13

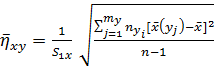
Якщо генеральна сукупність підпорядковується хоча б приблизно двомірному нормальному розподілу й число іспитів не менше 30-40, то середнє квадратичне відхилення емпіричного коефіцієнта кореляції визначається за приближеною формулою

При n > 70-80 величина 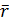приблизно підпорядковується нормальному розподілу, що дозволяє оцінювати коефіцієнт кореляції за допомогою довірчої ймовірності.

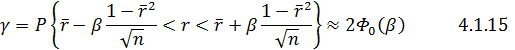
При невеликому об’ємі вибірки застосовується рівність

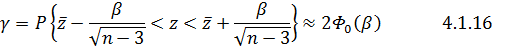
Де 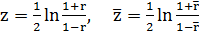. 4.1.17

Значення z у залежності від r наведені у довідниковій таблиці значень функції .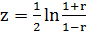

Приклад 2. У результаті обробки n = 200 незалежних іспитів отримана кореляційна таблиця для межі текучості u (кг/мм²) і межі міцності υ сталі (табл. (4.1.5). Випадкові коливання значень цих величин та похибка їх вимірювання підпорядковується нормальному закону. Необхідно визначити коефіцієнт кореляції між u та υ, кореляційні відношення υ на u та τ на v і довірчій інтервал для коефіцієнта кореляції при довірчій ймовірності γ = 0,95.

Табл.4.1.5

Результати обробки n = 200 незалежних іспитів

υ u

Для спрощення обчислювання проводимо лінійну заміну.

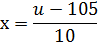
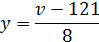
Яка приводить до кореляційній табл. 4.1.6. число розрядів у таблиці: m_x=4, m_y =5.

Табл. 4.1.6.

Кореляційна таблиця

Обчислюємо частоти і умовні середні за формулами (4.1.3) – (4.1.5). Результати наведені у табл. 4.1.6. Потім обчислюємо вибіркові вибіркові середні за формулою(4.1.8) і (4.1.9) та вибіркові середніх коефіцієнтів відхилень, використовуючи формули (4.1.10) і (4.1.11). У результаті отримуємо 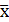= 0,560, = - 0,105; S_ix = 0,692; S_iy = 0,779.

Для обчислення розрахунків записуємо у верхньому правому куті табл. 4.1.7. добуток х_іу_j й обчислюємо:

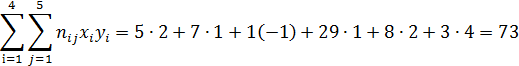
Підставимо отримані значення у формулу (4.1.12), отримуємо 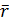= 0,791. Обчислення кореляційних відношень за формулами (4.1.13) призводить до 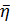_ух= 0,791;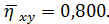

Об’єм виборки є достатнім для можливості використання формули (4.1.15), з якої слідують 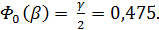З таблиці довідника щодо значень функції 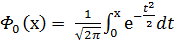знаходимо β= 1,96. Тобто з ймовірністю 0,95 виконується нерівність у фігурних дужках формули (4.1.15), яке після обчислення призводить до

0,739< r < 0,843 (4.1.18)

Для порівняння проведемо оцінювання за формулою (4.1.16). Використовуючи таблицю значень функції 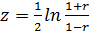по r = 0,791 знаходимо z =1,074. При β = 1,96 з (4.1.16) знаходимо з табл. для z відповідне значення r й останню нерівність записуємо у вигляді

0,732 < r < 0,838 (4.1.19)

Близькість оцінок (4.1.18) та (4.1.19) пояснюється тим, що n є невеликим.

При малих n точність визначення r різко падає й може виникнути сумнів у корельованості випадкових величин х і у, незважаючи на те, що емпіричний коефіцієнт кореляції достатньо великий. Для перевірки гіпотези про відсутність кореляційного зв’язку (r = 0) служить вираз

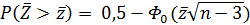(4.1.20)

Де 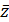- величина, що визначається за формулою (4.1.17).

Якщо ймовірність Р менша за прийнятий рівень значущості Р_δ, то гіпотеза про відсутність кореляційного зв’язку відкидається.

Необхідно відмітити, що для застосування виразів (4.1.15), (4.1.16), (4.1.20) достатньо, щоб розподіл, яке відповідає генеральній сукупності, що досліджується, був близький кожного із складових х і у до нормального не є доказом близькості самого двомірного розподілу до нормального.

Контрольні запитання та завдання

1. Що виявляє кореляційний аналіз та які його головні завдання?

2. Властивості коефіцієнта кореляції.

3. Як побудувати й для чого використовується графік «кореляційне поле»?

4. Оцінити щільність зв’язку між змінними

4.1

х	1,8	1,6	2,8	2,9	3,0
у	18,2	17,2	27,8	25,9	27,2

4.2

х	2,6	1,8	1,6	1,9	2,9
у	24,1	18,6	17,2	22,8	25,9

4.3

х	1,6	1,7	2,1	2,8	2,9
у	17,4	18,3	20,5	25,5	30,6

5. Поле кореляції Y та Х приведено у таблицях а), б), в).

5.1. Оцінити щільність та напрямок зв’язку між змінними за допомогою коефіцієнта кореляції, перевірити значущість коефіцієнта кореляції та побудувати для нього 95% - й довірчий інтервал.

5.2. Обчислити емпіричні кореляційні відношення та оцінити їх значущість на 5% - му рівні.

5.3. На рівні значущості 0,05 перевірити гіпотезу про лінійну кореляційну залежність.

а) б)

у х	0-5	5-10	10-15	15-20
0-1
1-6
6-10
10-14

у х	6-10	10-14	16-20	20-24
0-5
5-10
10-15
15-20

в)