Косвенный метод наименьших квадратов (КМНК) и его использование для определения параметров СЛОУ

Данный метод рассматривается на примере определения параметров функции потребления простой кейнсианской модели

C_t=α+β*y_t + U_t (1)

{

y_t=C_t+I_t (2)

C_t=α/(1-β) + β*I_t/(1-β) + U_t/(1-β)

α׳= α/(1-β) (3)

β׳=β/(1-β) (4) C_t=α׳+β׳*I_t+U׳_t (5)

в уравнении (5) слева имеем только экзогенные переменные и к нему может быть применён стандартный МНК и найдены оценки α׳ и β׳

Используя эти оценки из уравнения (3) и (4) можно найти оценки

α= α׳/(1+ β׳) β= β׳/(1+ β׳) Это и есть КМНК

1. исходная структурная система уравнений преобразуется в систему приведённых уравнений. Используя ее МНК находим несмещённые оценки коэффициентов приведённой системы уравнений.

2. используя соотношение ((3), (4)) между коэффициентами приведённой системы уравнений и структурной системы уравнений находим коэффициенты структурной системы уравнений.

Если число коэффициентов приведённой системы уравнений равно числу коэффициентов исходной структурной системы уравнений, то система уравнений считается идентифицируемой.

Если число коэффициентов уравнений будет < числа коэффициентов структурной системы уравнений, то система уравнений является не идентифицируемой.

Если число коэффициентов приведённой системы уравнений > числа коэффициентов структурной системы уравнений, то в этом случае имеем сверх идентифицируемую систему уравнений. И эта система может быть несовместной.

14.4 Метод инструментальных переменных (МИП) и его применение для параметров уравнения регрессия (общий случай)

При наличии ошибок измерения, если их причина заключается в том, что измеряемая переменная принципиально отличается от истинной объясняющей переменной в уравнении, то можно попытаться заменить её более подходящей переменой.

Для этой цели используем МИП, который заключается в частичной замене непригодной объясняющей переменной такой переменной, которая существенным образом отражала воздействие на Y исходной объясняющей переменной, но не коррелированна со случайной составляющей.

Таким образом в практике возникают 2 случая необходимости использования МИП: 1)когда используемая объясняющая переменная может быть измерена с большими ошибками или вообще неизмерима и она заменяется другой объясняющей переменной. 2)если объясняющая переменная но коррелирует существенным образом со случайной составляющей.

В обоих случаях необходимо найти замену исходной объясняющей переменной и новая переменная должна:

а) коррелировать существенным образом с заменяемой объяснительной переменной

б) не коррелировать со случайной составляющей

y=α+β*x+U В качестве исходной переменной – x, заменяемой z.

В этом случае величина β инструментальных переменных определяется

βип= cov(y;z) / cov(x;z)

При больших выборках βип=cov(y;z) / cov(x;z) = сov[(α+β*x+u);z] / cov(x;z) =

=( cov(α;z) + cov(β-x;z) + cov(u;z) )/ cov(x;z) = β + (cov(u;z) / cov(x;z))

Для достаточно больших выборок cov(u;z) =>0 а cov (x;z), при условии, что x и z достаточно сильно коррелируют между собой, стремится к истинному значению.

Поэтому, чем выше корреляция между x и z тем выше будет совпадение оценок инструментальной переменой и обычного МНК.

Однако, если корреляция между x и z будет приближаться к 1 функциональной зависимости то есть опасность, что z начнёт коррелировать со случайной составляющей.

Метод инструментальной переменной (МИП) и его применение для СЛОУ.

МИП в частности может быть использован как

С_t=α+β*y_t+U_t

{

y_t=C_t+I_t

В данном случае определению параметров из уравнения потребления мешает то, что величина Yt коррелирует со случа2ной составляющей и необходимо найти такую переменную которая коррелировала бы с Yt существенным образом, но не корелировала бы со случайной составляющей.

В качестве такой величины можно использовать инвестиции.

C_t=α+β*I_t+U_t

В этом случае b_ип=cov(C_t,I_t) / cov(y_t,I_t)

b_кмнк=b׳/(1+b׳)= ( cov(C_t;I_t)/var(I_t))/ (cov(C_t;I_t)/var(I_t)) =cov(C_t;I_t) / (var(I_t)+cov(C_t;I_t))

y_t=C_t+I_t => cov(y;I)=cov[(C+I);I]=cov(C_t;I_t)+var(I) => b_ип=b_кмнк

Идентифицируемость СЛОУ.

Рассмотрим проблему идентификации на примере линейных уравнений.

y₁=α+β₁*x₁+β₂*x₂+β₃*y₂+U₁

{

y₂=j+β₄*x₄+β₅*y₁+U₂

y₁=α+β₁*x₁+β₂*x₂+β₃*j+β₃*β₄*x₄+β₃β₅*y₁

y₁=(α+β₃*j)/(1-β₃*β₅) + β₁*x₁/(1-β₃*β₅) + β₂*x₂/(1-β₃*β₅) + β₃*β₄*x₄/(1-β₃*β₅)

y₂=j+β₄*x₄+β₅*α+β₅*β₁*x₁+β₅*β₂*x₂+β₅*β₃*y₂

y₂=(j+β₅*α)/(1-β₅*β₃) + β₄*x₄/(1-β₅*β₃) + β₅*β₁*x₁/(1-β₅*β₃) +β₅*β₂*x₂/(1-β₅*β₃)

y₁=α׳+β׳₁*x₁+β׳₂*x₂+β׳₃*x₄+U׳₄

{ (2)

y₂=j׳+β׳₄*x₄+β׳₅*x₁+β׳₆*x₂+U׳₂

К системе уравнений (2) можно применить МНК и получить несмещенные, состоятельные и эффективные оценки.

Однако определить коэффициенты исходной структурной системы уравнений не представляется возможности.

В системе ур. (1) имеет 7 неизвестных коэффициентов, а с помощью МНК из приведённой системы уравнений получим 8 коэффициентов.

Следовательно для 7 неизвестных получим 8 уравнений т.е. система будет сверхидентифиуированна.

В этом случае один коэффициент может быть получен двумя способами и получены различные её значения. В связи с этим необходимо выработать правило проверки идентифицируемости исходной структурной системы уравнений.

Для того, чтобы система уравнений была полностью идентифицируема, неоюходимо чтобы количество коэффициентов приведённой системы уравнений равнялось числу коэффициентов структурной системы уравнений.

Если исходная структурная система уравнений состоит из неидентифицируемых уравнений состоит из неидентифицируемых уравнений то вся система будет неидентифицируема.

Если система уравнений содержит одно не идентифицируемое, 2 сверх идентифицируемое, то система Ур-ий в целом будет идентифицируема.

Необходимым условием идентификации уравнения является выполнение следующего простого счетного правила:

D+1=H - уравнение идентифицируемое

{ D+1<H - уравнение неидентифицируемое

D+1>H - уравнение сверхидентифицируемое

где Н – число эндогенных переменных в уравнении, D – число экзогенных переменных в системе ур-ий не входящих в данное уравнение.

14.7 Двухшаговый метод наименьших квадратов.

Имеется система линейных одновременных уравнений.

1 шаг) Исходную систему линейных уравнений приводим к приведенной форме уравнения и, применяя метод наименьших квадратов получаем оценки коэффициентов приведенной системы уравнений.

2 шаг) Используя найденные коэффициенты приведенной системы уравнений и значения экзогенных переменных, находим теоретические значения эндогенных переменных. Эти значения переменных подставляем в исходную систему одновременных уравнений вместо фактических значений эндогенных переменных в правой части уравнения.

Т.к. теоретические значения эндогенных переменных не зависят от случайной составляющей. К исходной системе одновременных уравнений можно применить МНК и найти оценки параметров исходной системы уравнений.

Трехшаговый МНК.

В тех случаях, когда:

А) коэффициенты системы одновременных уравнений связаны между собой дополнительными связями или имеется три уравнения, связывающие эндогенные переменные между собой. В этих случаях используют ТМНК. Это вызвано тем, что параметры уравнения из систем уравнения находятся отдельно, сначала для первого, затем для второго без учета взаимосвязи между уравнениями.

Б) в этом случае может создаваться ситуация, когда доп. Связи между коэф. будут нарушаться, хотя оценки параметров будут несмещенными, состоятельными и эффективными. Чтобы учесть эти дополнительные ограничения и используется трехшаговая процедура нахождения параметров

Первые два шага аналогичны ДМНК, затем делается третий шаг: после определения параметров системы одновременных уравнений производится увязка систем уравнений между собой. В качестве меры связи обычно выступает ковариация ошибок

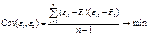
Минимум ковариации ошибок достигается путем пересчета коэффициентов уравнения регрессии.