Скалярное поле. Производная скалярного поля по направлению

Определение. Полем называется часть пространства, каждой точке которого поставлено в соответствие определенное значение некоторой физической величины.

Если физическая величина скалярная, то поле называется скалярным, а если векторная, то векторным.

Примерами скалярных полей могут служить поле распределения температуры, поле распределения потенциала в электрическом поле и т.д.

Примерами векторных полей служат: силовое поле, поле скоростей текучей жидкости, магнитное поле и т.д.

Скалярное поле считается заданным, если в каждой точке P определена скалярная функция u (P) , называемая функцией поля.

Иногда пишут u (x, y, z).

Определение Поверхностью уровня скалярного поля называют геометрическое место точек, в которых функция u принимает постоянное значение, т.е.

u (x, y, z) = C

Если в частном случае скалярное поле плоское, т.е. мы изучаем распределение значений физической величины в какой-то плоской области, то функция поля u зависит от двух переменных, например х и у. Линиями уровня этого поля будут линии уровня функции u (x, y)

u (x, y) = C

Важной характеристикой скалярного поля является скорость изменения функции поля в заданном направлении.

Пусть нам задана функция поля u (x, y, z).

Возьмем т. Р(x, y, z) и какой-нибудь луч , из нее выходящий. Направление этого луча зададим углами α, β, γ, которые он образует с направлением осей ox, oy, oz.

Если - единичный вектор, направленный по лучу λ, то его проекциями будут направляющие косинусы

Пусть т. Р₁(x₁, y₁, z₁) лежит на луче λ , Расстояние РР₁ обозначим через ρ. Проекции вектора на оси координат будут, с одной стороны, равны

ρ cos α, ρ cos β, ρ cos γ,

а с другой стороны – разностям x₁ – x, y₁ – y, z₁ – z.

Следовательно,

Рассмотрим теперь приращение функции u при переходе из т. Р в т. Р₁

Если т. Р будет изменять свое положение на луче λ, то в выражении для разности u(P₁) – u(P) будет меняться только величина ρ.

Составим отношение и перейдем к пределу при , предполагая, что этот предел существует.

Определение.Предел

(1)

называется производной от функции u(x, y, z) по направлению λ в т. Р.

Этот предел будем обозначать символом 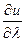или

Величина его зависит от выбранной т. Р(x, y, z) и от направления луча λ,

т.е. от α, β, γ.

Если т. Р фиксирована, то величина производной 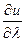будет зависеть только от направления луча λ.

Из определения производной по направлению следует, что если направление λ совпадает с положительным направлением оси ох,

т.е. , , то lim (1) будет просто равен частной производной от функции u(x, y, z) по х:

Аналогично получаем частные производные ,

Подобно тому как частные производные , , характеризуют скорость изменения функции u в направлении осей координат, так и производная по направлению 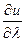будет являться скоростью изменения функции поля u(x, y, z) в т. Р по направлению луча λ. Абсолютная величина производной 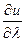по направлению λ определяет величину скорости, а знак производной характер изменения функции u (возрастание или убывание).

Вычисление производной по направлению производится при помощи следующей теоремы:

Теорема: Для всякой дифференцируемой функции u(x, y, z) существует производная по любому направлению λ, причем

,

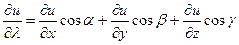где cos α, cos β, cos γ – направляющие косинусы луча λ.

Доказательство. Полное приращение для функции u (x, y, z) будет

,

где Е – бесконечно малая величина более высокого порядка, чем ρ. Полагая , , , получим

причем при .

Разделим обе части последнего равенства на ρ

Переходя к пределу при , получим:

ч.т.д.

Пример: Дана функция u = xyz. Найти ее производную в т. Р(5, 1, 2) в направлении, идущем от этой точки к точке Q(7, -1, 3).

Находим частные производные функции u = xyz

, , и вычислим их значения в т. Р

, , , то

, ,

Следовательно

Знак минус указывает, что в данном направлении функция убывает.

Если поле плоское, то направление луча λ вполне определяется углом α его наклона к оси абсцисс. Формулу для производной по направлению можно получить из общей формулы, положив ,

Тогда

Если α = 0, то ,

если , то