Ударное нагружение элементов машин, представляемых в виде систем

С распределенными массами

Продольный удар

Призматические или цилиндрические элементы машин (трубы, колонны, стойки, канаты и т.п.) могут быть приближенно представлены в виде стержня постоянного сечения, жестко закрепленного одним концом (рис. 38).

Пусть груз массой m движется со скоростью u₀ в направлении оси стержня. После соударения груза со стержнем в месте соударения возникает деформация, которая распространяется волнообразно вдоль стержня, отражается от закрепленного конца и движется к свободному концу, затем снова распространяется в сторону закрепленного конца и т.д.

Движение сечений стержня описывается уравнением волнового типа (289). Решение этого уравнения может быть получено с помощью разрывных функций. Обычно перемещение сечений стержня U находят в виде

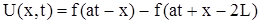, (314)

где 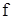– произвольная функция, выражающая характер движения деформации.

Первый член правой части (314) соответствует движению волны деформации в направлении оси x (от 0 до l на рис. 38), а второй – в обратном направлении.

Полагая, что после соударения груз движется вместе со свободным концом стержня, для сечения, соответствующего 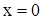, имеем

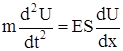. (315)

Если выразить 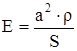, где 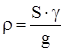- погонная масса стержня, и обозначить 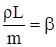, то

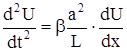. (316)

Подставляя значение U из выражения (314)

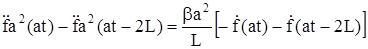, (317)

преобразуя и сокращая, получим

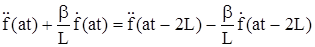. (318)

До соударения груза и стержня для всех сечений последнего 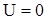. Следовательно, при 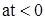имеем .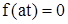

Для интервала 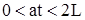правая часть уравнения (318) равна нулю. Тогда

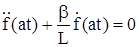. (319)

Проинтегрировав (319) в пределах 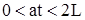, получим

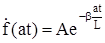. (320)

При 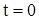свободный конец стержня 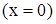имеет скорость 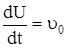. Введем это условие в уравнение (314):

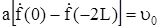, (321)

поскольку 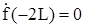, то .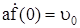

Подставляя 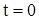, находим 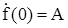или .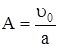

Теперь

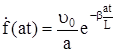. (322)

В соответствии с граничными (концевыми) условиями для интервала 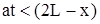функцию 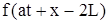следует принять равной нулю.

Тогда выражение (314) будет иметь вид

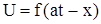, (323)

а относительная деформация стержня

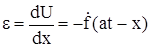. (324)

Подставляя выражение (322), получим

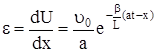(325)

и скорость деформации

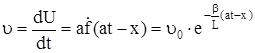. (326)

Относительная деформация стержня и скорость этой деформации в любом сечении связаны при первом прохождении волны деформации зависимостью 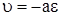. Следовательно, деформация стержня в момент удара полностью определяется скоростью ударяющего груза u₀ и не зависит от его массы m. Если 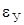– относительная деформация, соответствующая пределу упругости, то максимально допустимая скорость удара равна

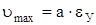. (327)

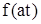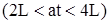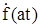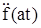Для определения функции в следующем интервале воспользуемся уравнением (318), в первую часть которого подставим значения и при .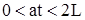

Тогда

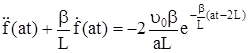. (328)

При неразрывном (совместном) движении груза и свободного конца стержня скорость не может изменяться скачкообразно. Следовательно, при 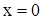выражение

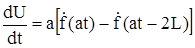(329)

должно быть непрерывной функцией.

Условие непрерывности удовлетворяется, если разрывы функции 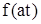повторяются при каждом изменении at на величину 2L. При 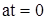функция 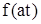скачкообразно увеличивается на величину 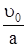. Такие же скачки повторяются при 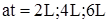и т.д.

При 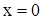конец первого интервала определяется равенством 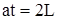. При этом, согласно (322),

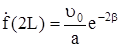. (330)

В то же время происходит скачкообразное изменение функции 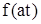, после чего 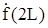увеличивается на :

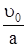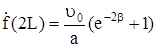. (331)

Выражение (331) является начальным условием для интегрирования уравнения (328). Используя (331) для определения постоянной интегрирования при 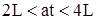, получим

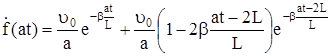. (332)

Аналогично для интервала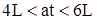

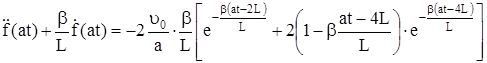, (333)

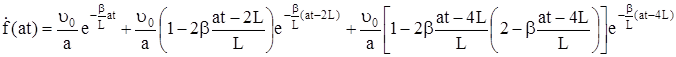(334)

Так же можно определить значение для последующих интервалов.

Из выражения (314) относительная деформация стержня

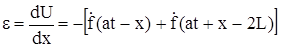. (335)

Подставляя соответствующие очередным интервалам и определяемые формулами (322), (332) и (334), получим значение e для тех же интервалов и любых сечений стержня (любых x).

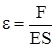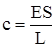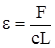Так как и линейная жесткость , то или

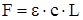, (336)

где F – усилие, действующее в рассматриваемом сечении.

На основе изложенных решений получены упрощенные формулы для определения максимальных ударных нагрузок стержня:

при 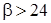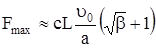; (337)

при 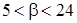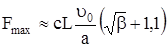; (338)

при 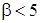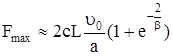. (339)

Если стержень расположен вертикально и ударная нагрузка вызывается свободно падающим грузом, то к значениям F, определяемым перечисленными формулами, следует прибавить вес груза.

Поперечный удар

Несущие части машин (крановые мосты, фермы и т.п.) приближенно можно представить в виде балки постоянного сечения (рис. 39).

В большинстве случаев достаточно точно можно рассмотреть процесс ударного нагружения и определить максимальные нагрузки такой системы путем предварительного приведения распределенных систем к системам с сосредоточенными массами (п. 12.1). Однако иногда требуется большая точность.

В этом случае задача сводится к рассмотрению волнового уравнения вида (289). Общее решение уравнения указанного типа относительно деформации балки U при воздействии на ее середину возмущающей силы P может быть получено аналогично показанному выше. Это решение имеет вид

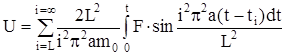, (340)

где 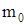– масса балки;

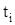– время, для которого определяется U;

.

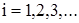В случае ударного нагружения сила F – величина, переменная во времени.

Если 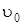– скорость соударения груза с балкой в начальный момент,

m – масса груза,

то скорость груза после соударения в любой момент 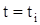равна

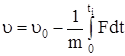. (341)

Перемещение груза в направлении удара

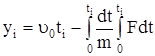. (342)

Деформации (изгиб) балки могут быть соизмеримы с контактными деформациями (сжатие) в месте соударения груза и балки, поэтому последние следует учитывать.

Известно, что контактная деформация

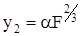, (343)

где 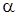– коэффициент, зависящий от кривизны поверхностей тел в месте контакта и механических свойств материала.

Например, для сферических поверхностей с радиусами кривизны R₁ и R₂

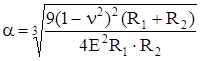, (344)

где 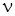– коэффициент Пуассона.

Если груз имеет сферическую поверхность с радиусом R, а балка в месте соударения – плоскость, то

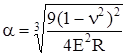. (345)

Если после удара груз не отделяется от балки до момента, когда последняя получит максимальную деформацию, то можно записать 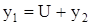, т.е.

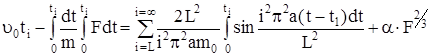. (346)

Решение уравнения (346) осуществляется численным методом путем итерации. Время от 0 до t нужно разделить на малые промежутки, подставляя которые можно получить соответствующие значения F и характер изменения этой величины во времени.