Кромки которых свободно оперты
Рассмотрим пластину, у которой две противоположные кромки свободно оперты, а две другие устроены как угодно. Пусть кромки х = 0 и х = а свободно оперты.
Будем искать решение дифференциального уравнения изгиба (176) в виде ряда
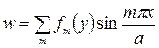 (206)
(206)
удовлетворяющего граничным условиям при х =0 и х = а.
Неизвестные функции fm(у), входящие в выражение упругой поверхности пластины, определим, подставляя выражение (206) в дифференциальное уравнение (176).
Сделав указанную подстановку, запишем
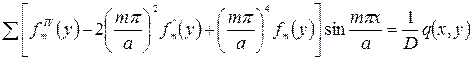 (207)
(207)
Для того чтобы получить дифференциальное уравнение, определяющее функции (у), разложим нагрузку q(х,у) в тригонометрический ряд по синусам аргумента а
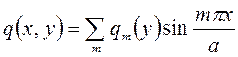 (208)
(208)
где
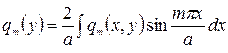 (209)
(209)
Подставляя разложение (208) в равенство (207), нетрудно получить дифференциальное уравнение
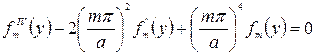 (210)
(210)
Уравнение (210) есть обыкновенное линейное дифференциальное уравнение четвертого порядка с постоянными коэффициентами. Общий интеграл этого уравнения можно записать, если будет найден общий интеграл соответствующего однородного уравнения и частное решение.
Интеграл однородного уравнения
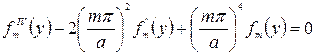 (211)
(211)
может быть получен при помощи подстановки
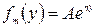 (212)
(212)
Подставляя выражение (212) в уравнение (211) и сокращая на неравный нулю множитель 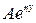 получим, что неизвестная величина
получим, что неизвестная величина 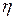 должна удовлетворять следующему характеристическому уравнению:
должна удовлетворять следующему характеристическому уравнению:
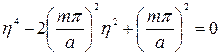
Так как корни этого уравнения кратны и попарно равны
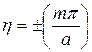 ,
,
то решение однородного уравнения (211) можно записать следующим образом:
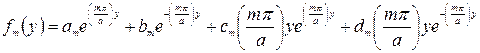 (213)
(213)
или, переходя к гиперболическим функциям, -
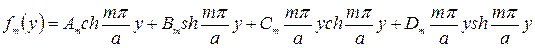 (214)
(214)
Общий интеграл дифференциального уравнения (210) запишется в виде
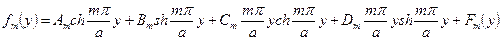 (215)
(215)
где 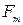 (у) — частное решение дифференциального уравнения (210).
(у) — частное решение дифференциального уравнения (210).
Входящие в выражение (215) постоянные интегрирования должны быть определены из условий закрепления опорных кромок пластины у=0 и у=b. Для каждой из этих кромок, как было указано выше, всегда может быть выписано по два граничных условия и, следовательно, всегда можно записать достаточное число уравнений для определения этих постоянных.
Применим изложенное решение для различных частных случаев изгиба пластины.
П р и м е р 1. Рассчитать пластину, свободно опертую по всем четырем кромкам и загруженную равномерно распределенным давлением .
В рассматриваемом случае q(х,у)=q=const, и, следовательно, коэффициенты разложения этой нагрузки в ряд по синусам кратного аргумента на основании формулы (209) будут
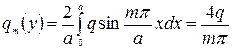 (216)
(216)
При m=1,3,5….
Так как правая часть дифференциального уравнения, определяющего функции fm(у), в этом случае равна постоянной величине и среди корней характеристического уравнения нет нулей, то частное решение можно отыскать также в виде постоянной величины. Подставляя это частное решение в дифференциальное уравнение (210) и принимая во внимание формулу (216), получим
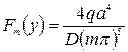 (217)
(217)
При m=1,3,5…
Подстановка формулы (217) в общий интеграл (215) дает
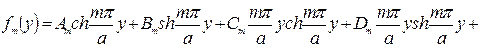
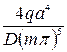 (218)
(218)
Примем начало координат по середине кромки х=0 (рис. 31). Тогда, учитывая, что прогиб пластины будет симметричным относительно оси ох, следует в выражении (218) коэффициенты при нечетных функциях положить равными нулю.
Принимая Вm, = Сm, =0, получим
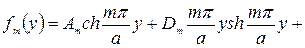
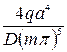 (219)
(219)
m=1,3,5...
Постоянные Аm и Dm, должны быть определены из граничных условий для функций fm(у) при у = 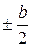 . Найдем эти граничные условия.
. Найдем эти граничные условия.
Так как для свободно опертой кромки у = 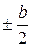 прогиб пластины w должен удовлетворять условиям
прогиб пластины w должен удовлетворять условиям
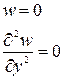
то, подставляя сюда выражение (206), получим
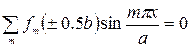
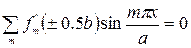
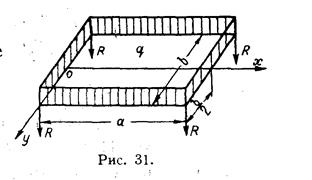
Последние два равенства могут быть выполнены лишь при условии
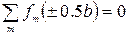
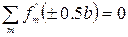
Используя эти граничные условия, запишем следующую систему алгебраических уравнений1 определяющую постоянные Аm и Dm
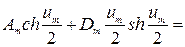
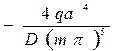
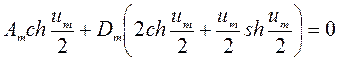
где введено обозначение
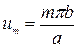
Решая полученную систему уравнений, найдем
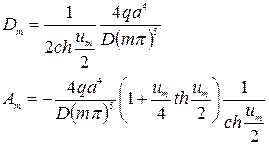
Следовательно,
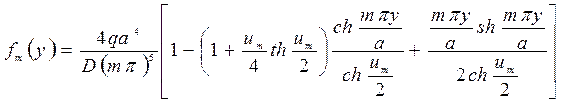
и прогиб пластины будет
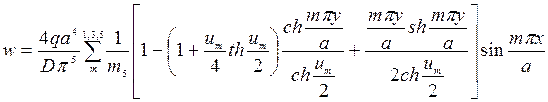 (220)
(220)
Ряд (220) сходится довольно быстро, но его сходимость можно еще более усилить. Действительно, рассмотрим пластину, у которой отношение сторон 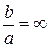 . Изгиб ее можно характеризовать изгибом балки-полоски, длина которой равна а. Дифференциальное уравнение изгиба балки-полоски будет
. Изгиб ее можно характеризовать изгибом балки-полоски, длина которой равна а. Дифференциальное уравнение изгиба балки-полоски будет
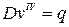
Так как на опорах балка свободно оперта, то решение этого дифференциального уравнения можно искать в виде
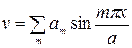
Представляя нагрузку в виде ряда
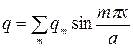
и внося разложение v и q в дифференциальное уравнение, найдем
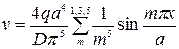
С другой стороны, нетрудно получить следующее выражение упругой линии в замкнутом виде (см. [41]):
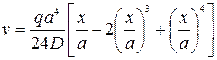
Сравнивая два последних выражения для упругой линии балки, запишем
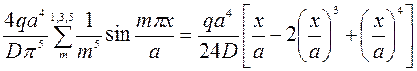 (221)
(221)
Полученное выражение позволяет переписать формулу (220) в виде
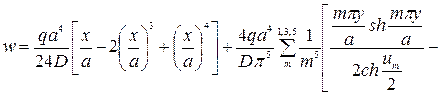
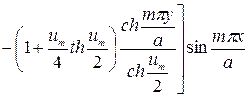 (222)
(222)
На основании сказанного можно сделать заключение, что второй член в правой части выражения (222) учитывает влияние на изгиб пластины ограниченности ее размеров в направлении оси оу.
Зная выражение для прогиба пластины, нетрудно определить и другие элементы ее изгиба.
Изгибающие и крутящие моменты можно вычислить по формулам (137), а интенсивность поперечных усилий (г1 и r2)— по формулам (164).
Для определения углов поворота сечений пластины следует продифференцировать выражение (222) по соответствующей координате. В частности, углы поворота кромок пластины у = 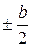 будут определяться формулой
будут определяться формулой
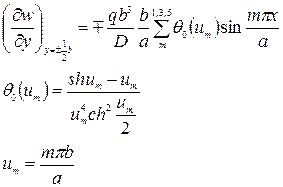 (223)
(223)
Углы поворота кромок х=0 и у=0, разложенные в ряд по синусам аргумента 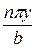 , можно получить, если в формуле (223)
, можно получить, если в формуле (223) 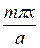 заменить на
заменить на 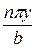 , а размер а размером b, т. е.
, а размер а размером b, т. е.
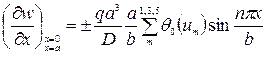 (224)
(224)
где
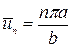
Для практических расчетов необходимо знать наибольшие значения прогиба, изгибающих моментов, реакций опорного контура и т. д.
Напряжения изгиба вычисляются по формуле
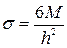 (225)
(225)
где 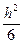
 — момент сопротивление балки-полоски единичной ширины. Указанные величины могут быть определены по следующим формулам.
— момент сопротивление балки-полоски единичной ширины. Указанные величины могут быть определены по следующим формулам.
Наибольшая стрелка прогиба будет в центре пластины
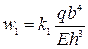 (226)
(226)
Изгибающие моменты М1 в центре пластины в сечениях, перпендикулярных оси ох, и М2— в сечении, перпендикулярном оси оу—
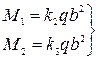 (227)
(227)
Наибольшие значения перерезывающих сил будут по середине опорных кромок пластины, т. е. N1 на кромках х=0; х=а и N2 на кромках у = 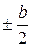 ;
;
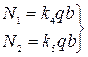 (228)
(228)
Наибольшие значения реакций опорных кромок будут по середине этих кромок, г1—на кромках х = 0 и х= а; r2 на кромках у = 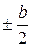 ;
;
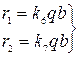 (229)
(229)
Сосредоточенные реакции в углах пластины (направление этих реакций для рассматриваемой задачи показано на рис.31)
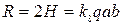 (230)
(230)
Входящие в формулы (226) — (230) коэффициенты k1 определяются по табл.6 в зависимости от отношения длинной стороны пластины а к короткой стороне b. Табл.6 вычислена при μ= 0,3 и заимствована из книги акад. Б. Г. Галеркина ,,Упругие тонкие плиты”.
Таблица 6
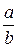 | 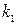 | 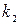 | 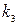 | 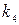 | 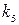 | 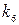 | 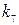 | 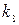 |
1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 3,0 4,0 5,0 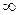 | 0,0433 0,0530 0,0616 0,0697 0,0770 0,0843 0,0906 0,0964 0,1017 0,1064 0,1116 0,1336 0,1400 0,1416 0, 1422 | 0,0479 0,0494 0,0501 0,0504 0,0506 0,0499 0,0493 0,0486 0,0479 0,0471 0,0464 0,0404 0,0384 0,0375 0,0375 | 0,0479 0,0553 0,0626 0,0693 0,0753 0,0812 0,0862 0,0908 0,0948 0,0985 0,1017 0,1189 0,1235 0,1246 0, 1250 | 0,338 0,315 0,294 0,275 0,258 0,242 0,228 0,216 0,205 0,194 0,185 0,124 0,093 0,077 — | 0,338 0,360 0,380 0,397 0,411 0,424 0;435 0,444 0,452 0,459 0,465 0,493 0,498 0,500 0,500 | 0,420 0,399 0,377 0,357 0,337 0,320 0,303 0,287 0,273 0,260 0,248 0,166 0,125 0,100 — | 0,420 0,440 0,455 0,468 0,478 0,486 0,491 0,496 0,499 0,502 0,503 0,505 0,502 0,501 0,500 | 0,065 0,064 0,063 0,062 0,059 0,057 0,055 0,053 0,050 Ю,048 0,046 0,032 0,024 0,019 — |
П р и м е р 2. Определить упругую поверхность пластины, свободно опертой на кромках х=0 и х=а и жестко заделанной на кромках у = 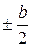 (рис. 32). Нагрузка, действующая на пластину, равномерно распределена по всей ее площади.
(рис. 32). Нагрузка, действующая на пластину, равномерно распределена по всей ее площади.
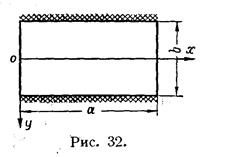
В рассматриваемой задаче прогиб пластины будет симметричен относительно оси ох и, следовательно, функции 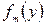 могут быть записаны в виде [см. формулу (219)]
могут быть записаны в виде [см. формулу (219)]
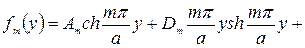
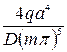 (231)
(231)
Входящие в это выражение постоянные интегрирования Аm и Dm, должны быть определены из условий для функций 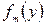 при у =
при у = 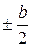 . Так как кромки у =
. Так как кромки у = 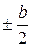 жестко заделаны, то нетрудно получить, что функции
жестко заделаны, то нетрудно получить, что функции 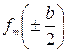 на этих кромках удовлетворяют условиям
на этих кромках удовлетворяют условиям
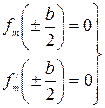
 (232)
(232)
Подчиняя выражение (231) граничным условиям (232), получим систему алгебраических уравнений для определения постоянных Am и Dm
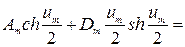
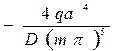
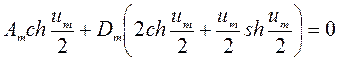
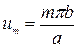
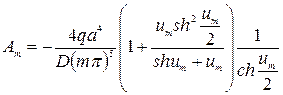
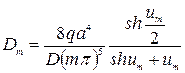
Подставляя найденные значения постоянных в выражение (231), запишем
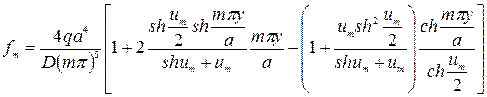
Прогиб пластины будет определяться формулой
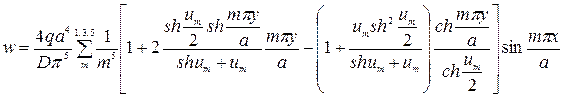 (233)
(233)
Используя равенство (221), формулу (233) можно переписать в виде
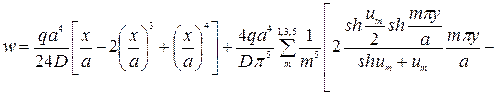
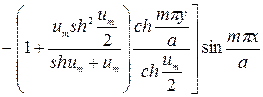 (234)
(234)
В полученном выражении второй член в правой части, как и раньше, учитывает влияние на прогиб пластины ограниченности ее размеров в направлении оси оу, а также заделку на кромках у = 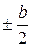 .
.
После того как определен прогиб пластины, можно получить формулы, определяющие остальные элементы ее изгиба. В частности, изгибающий момент на кромках у = 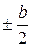 (в заделке) может быть определен по формуле
(в заделке) может быть определен по формуле
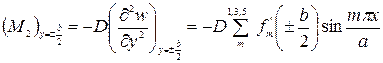
Дифференцируя два раза выражение (231) и подставляя уже найденные значения постоянных Аm и Dm получим
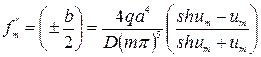 (235)
(235)
Следовательно, изгибающий момент в заделке будет
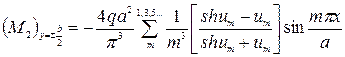 (236)
(236)
Необходимые для практических расчетов величины наибольших изгибающих моментов, а также наибольшая стрелка прогиба могут быть определены по формулам.
Стрелка прогиба в центре пластины
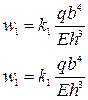

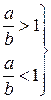 (237)
(237)
Изгибающие моменты в центре пластины: М1—момент в сечении, перпендикулярном оси ох; М2—момент в сечении, перпендикулярном оси оу:
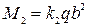
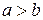 ;
;
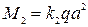
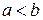 ; (238)
; (238)
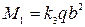
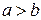 ;
;
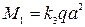
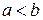
Изгибающий момент по середине жестко заделанных кромок
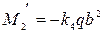
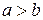
(239)
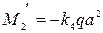
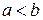
Входящие в формулы (237) —(239) коэффициенты ki определяются по табл. 7 в зависимости от отношения сторон пластины. Табл. 7 составлена для значения коэффициента Пуассона μ=0,3.
Таблица 7
| Отношение сторон пластины | 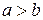 | 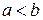 | ||||||
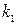 | 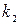 | 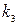 | 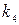 | 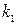 | 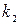 | 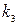 | 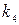 | |
1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 3,0 4,0 5,0 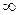 | 0,0214 0,0276 0,0349 0,0425 0,0504 0,0582 0,0658 0,0730 0,0799 0,0863 0,0987 0,1276 0,1383 0,1412 0,1422 | 0,0332 0,0370 0,0401 0,0426 0,0446 0,0460 0,0469 0,0474 0,0476 0,0476 0,0477 0,0421 0,0390 0,0379 0,0375 | 0,0241 0,0309 0,0377 0,0447 0,0517 0,0585 0,0650 0,0711 0,0768 0,0821 0,0869 0,1144 0,1223 0,1243 0,1250 | 0.0698 0,0788 0,0868 0,0938 0,0998 0,1049 0,1090 0,1124 0,1152 0,1173 0,1191 0,1246 0,1250 0,1250 0,1250 | 0,0214 0,0228 0,0243 0,0255 0,0262 0,0270 — — — — 0,0284 — — — 0,0284 | 0,0332 0,0356 0,0374 0,0388 0,0399 0,0406 — — — — 0,0421 — — — 0,0417 | 0,0244 0,0230 0,0216 0,0202 0,0189 0,0172 — — — — 0,0142 — — — 0,0125 | -0,0698 —0,0739 —0,0770 —0,0793 —0,0808 —0,0829 — — — — —0,0842 — — — —0,0833 |
