Непрерывность функции. Основные теоремы о непрерывных функциях
Понятие непрерывности функции является одним из основополагающих понятий в математическом анализе.
Пусть функция 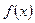 определенав некоторой окрестности точки
определенав некоторой окрестности точки 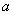 .
.
Определение
Функция 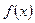 называется непрерывной в точке
называется непрерывной в точке 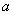 , если предел этой функции и ее значение в этой точке равны, т.е.
, если предел этой функции и ее значение в этой точке равны, т.е.
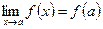 . . | (4.7.1) |
Так как 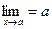 , то это равенство можно переписать в следующей форме:
, то это равенство можно переписать в следующей форме: 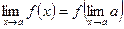 .
.
Определение непрерывности функции можно сформулировать как «на языке последовательностей», так и «на языке e–d » в соответствии с двумя определениями предела функции в точке. Приведем здесь второе из них.
Определение
Функция 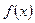 называется непрерывной в точке
называется непрерывной в точке 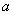 , если для любого
, если для любого 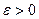 существует такое
существует такое 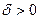 , что при всех
, что при всех 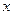 , удовлетворяющих неравенству
, удовлетворяющих неравенству 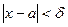 , выполняется неравенство
, выполняется неравенство 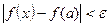 .
.
Определение
Функция 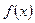 называется непрерывной справа (слева) в точке
называется непрерывной справа (слева) в точке 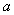 , если правый (левый) предел этой функции в точке
, если правый (левый) предел этой функции в точке 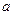 равен значению функции в этой точке.
равен значению функции в этой точке.
Символическая запись непрерывности функции справа и соответственно слева:
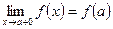 или или 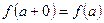 , , | (4.7.2а) |
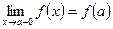 или или 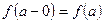 . . | (4.7.2б) |
Если функция 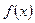 непрерывна в точке
непрерывна в точке 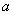 слева и справа, то она непрерывна в этой точке. В самом деле, функция
слева и справа, то она непрерывна в этой точке. В самом деле, функция 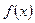 имеет предел в точке
имеет предел в точке 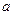 , который равен ее значению в этой точке, что и означает непрерывность функции при
, который равен ее значению в этой точке, что и означает непрерывность функции при 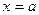 .
.
Для практического использования полезно сформулировать еще одно определение непрерывности функции.
Определение
Назовем разность 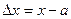 приращением аргумента в точке а, разность
приращением аргумента в точке а, разность 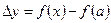 – приращением функции в точке
– приращением функции в точке 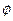 , обусловленным приращением аргумента
, обусловленным приращением аргумента 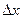 . Таким образом,
. Таким образом, 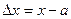 ,
, 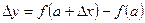 . Так как
. Так как 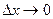 , то равенство (4.7.1) можно переписать в другой форме:
, то равенство (4.7.1) можно переписать в другой форме:
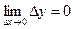 | (4.7.3) |
Теорема
Пусть функции 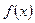 и
и 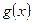 непрерывны в точке
непрерывны в точке 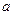 . Тогда функции
. Тогда функции 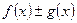 ,
, 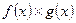 и
и 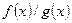 также непрерывны в точке
также непрерывны в точке 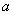 (частное при условии, что
(частное при условии, что 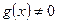 ).
).
Теорема
Если функция f(x) непрерывна в точке x0 и f(x0)>0, то существует такая окрестность точки x0, в которой f(x)>0.
Теорема
Если функция y=f(u) непрерывна в точке u0, а функция u=j(x) непрерывна в точке u0=j(x0), то сложная функция y=f[j(x)] непрерывна в точке x0, или
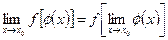 . . | (4.7.4) |
Точки разрыва функций и их классификация
Определение
Точками разрыва функции называются точки, в которых функция не определена или не является непрерывной.
Точки разрыва классифицируются следующим образом.
Устранимый разрыв
Точка 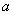 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции 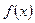 , если предел функции в этой точке существует, но в точке
, если предел функции в этой точке существует, но в точке 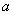 функция либо не определена, либо ее значение
функция либо не определена, либо ее значение 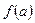 не равно пределу в этой точке.
не равно пределу в этой точке.
Пример
Функция 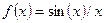 в точке
в точке 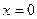 , как известно, имеет предел, равный единице. Однако в самой точке
, как известно, имеет предел, равный единице. Однако в самой точке 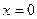 эта функция не определена. Этот разрыв можно устранить, если доопределить функцию в этой точке значением предела в ней:
эта функция не определена. Этот разрыв можно устранить, если доопределить функцию в этой точке значением предела в ней:
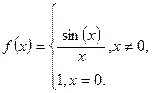
Доопределенная таким образом функция является непрерывной на всей числовой оси.
Разрыв 1–го рода
Точка 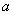 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции 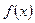 , если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы:
, если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы: 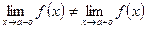 .
.
Типичным примером является функция 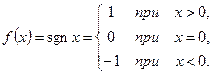 Для нее точка
Для нее точка 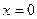 является точкой разрыва первого рода.
является точкой разрыва первого рода.
Разрыв 2–го рода
Точка 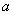 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции 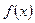 , если в этой точке функция
, если в этой точке функция 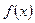 не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
1. Типичным примером является функция 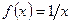 . Точка
. Точка 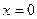 является точкой разрыва 2–го рода, так как
является точкой разрыва 2–го рода, так как 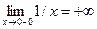 ,
, 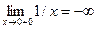
2. Для функции 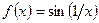 точка
точка 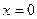 является точкой разрыва 2–го рода, так как ни левого, ни правого предела функции в этой точке не существует.
является точкой разрыва 2–го рода, так как ни левого, ни правого предела функции в этой точке не существует.
Кусочно–непрерывные функции
Функция 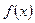 называется кусочно–непрерывной на отрезке
называется кусочно–непрерывной на отрезке 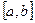 , если она непрерывна во всех внутренних точках
, если она непрерывна во всех внутренних точках 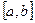 , за исключением, быть может, конечного числа точек, в которых имеет разрыв 1–го рода и, кроме того, односторонние пределы в точках
, за исключением, быть может, конечного числа точек, в которых имеет разрыв 1–го рода и, кроме того, односторонние пределы в точках 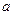 и
и 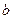 .
.
Упражнения
Вычислить указанные пределы:
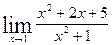 | 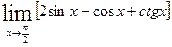 | ||
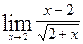 | 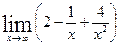 | ||
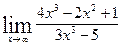 | 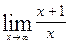 | ||
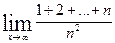 | 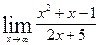 | ||
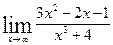 | 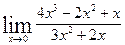 | ||
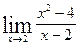 | 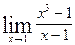 | ||
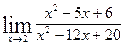 | 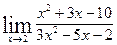 | ||
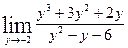 | 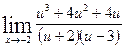 | ||
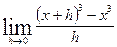 | 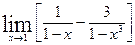 | ||
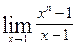 | 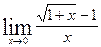 | ||
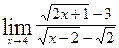 | 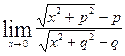 | ||
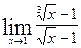 | 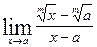 | ||
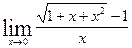 | 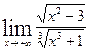 | ||
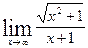 | 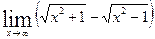 | ||
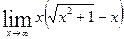 | 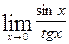 | ||
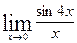 | 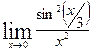 | ||
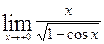 | 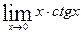 | ||
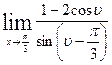 | 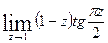 | ||
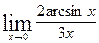 | 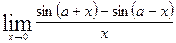 | ||
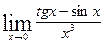 | 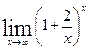 | ||
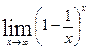 | 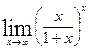 | ||
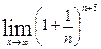 | 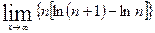 | ||
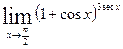 | 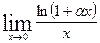 | ||
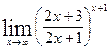 | 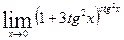 | ||
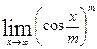 | 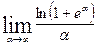 | ||
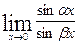 | 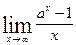 , , 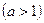 | ||
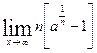 | 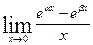 | ||
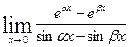 |
56. Определить точки разрыва функций:
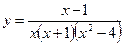 ,
, 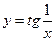 .
.
57. Найти точки разрыва функции 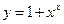 и построить график этой функции.
и построить график этой функции.
58. Между следующими бесконечно малыми (при 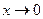 ) величинами
) величинами 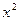 ,
, 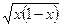 ,
, 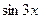 ,
, 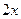 ,
, 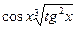 ,
, 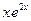 выбрать бесконечно малые одного порядка с бесконечно малой
выбрать бесконечно малые одного порядка с бесконечно малой 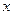 , а также высшего и низшего порядка, чем
, а также высшего и низшего порядка, чем 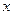 .
.
59. Среди указанных бесконечно малых (при 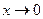 ) величин найти бесконечно малые, равносильные бесконечно малой
) величин найти бесконечно малые, равносильные бесконечно малой 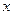 :
: 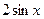 ,
, 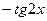 ,
, 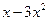 ,
, 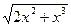 ,
, 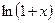 ,
, 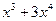 .
.
60. Убедиться в том, что при 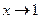 бесконечно малые величины
бесконечно малые величины 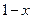 и
и 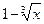 будут одного порядка малости. Будут ли они эквивалентны?
будут одного порядка малости. Будут ли они эквивалентны?
Глава 5. Производная
