Скорость распространения волн сжатия
В ряде случаев течения газа со сверхзвуковыми скоростями ( 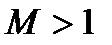 и
и 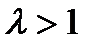 ) сопровождаются появлением ударных волн, вызывающих значительное сопротивление. Такое сопротивление часто называют волновым.
) сопровождаются появлением ударных волн, вызывающих значительное сопротивление. Такое сопротивление часто называют волновым.
Многочисленные эксперименты показали, что всякое повышение давления, которое возникло в каком-либо месте газовой среды, распространяется в ней с большой скоростью в виде волн давления. Слабые волны давления (характеризуемые малым повышением давления) движутся со скоростью звука. Сальные волны давления распространяются со скоростью, значительно превышающими скорость звука.
Одно из основных свойств сильных волн давления (ударных волн) заключается в том, что фронт волны очень узок (т.е. толщина этой волны бесконечно мала). Поэтому часто такую волну представляют как некоторую поверхность (как бы с двойным слоем), при пересечении которой параметры движущегося газа меняются скачкообразно.
Найдем скорость распространения волн сжатия. Для этого представим себе (рис. 8.1), что в трубе постоянного сечения  возникла и распространяется слева направо волна сжатия. Это может произойти, например, в результате мгновенного смещения поршня или взрыва. Пусть в момент времени
возникла и распространяется слева направо волна сжатия. Это может произойти, например, в результате мгновенного смещения поршня или взрыва. Пусть в момент времени  фронт волны сжатия совпадает с сечением 1-1. За бесконечно малый промежуток времени
фронт волны сжатия совпадает с сечением 1-1. За бесконечно малый промежуток времени 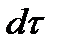 фронт волны переместился на расстояние
фронт волны переместился на расстояние 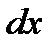 .
.
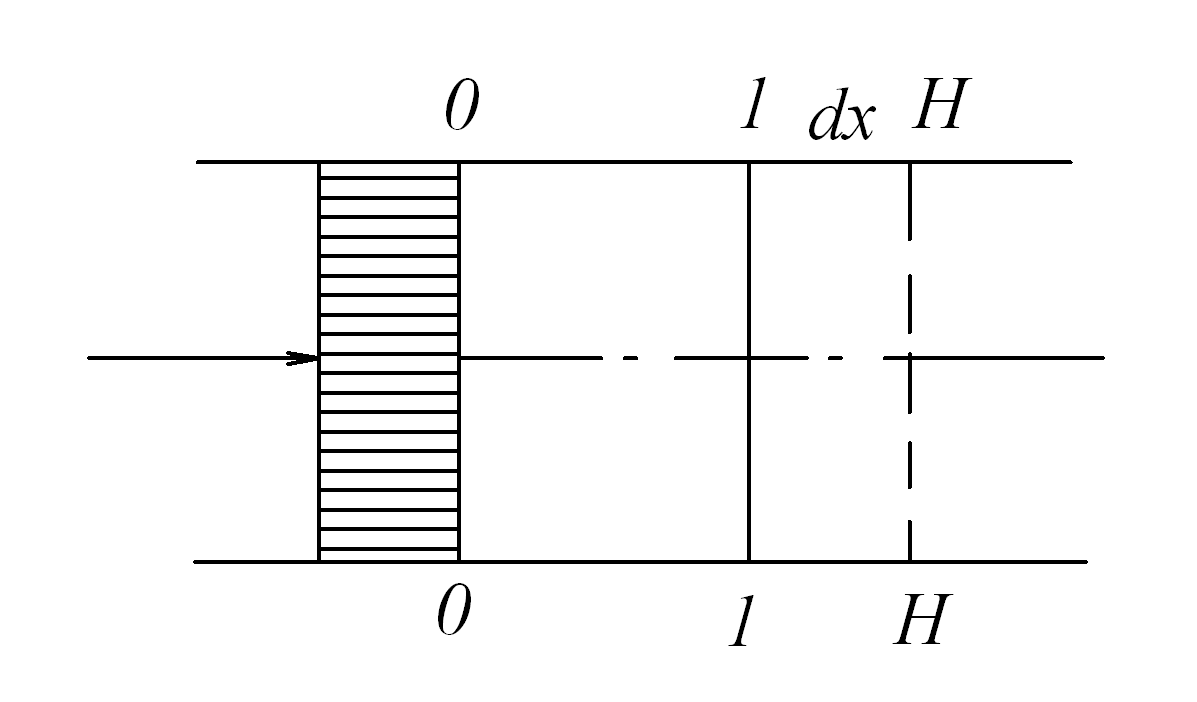
Рис. 8.1. К выводу скорости распространения волн сжатия
Это означает, что в области 1-Н за время 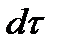 произошло повышение давления от величины
произошло повышение давления от величины 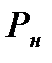 (давление невозмущенного газа) до величины
(давление невозмущенного газа) до величины 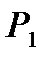 (давление за фронтом сжатия). В соответствии с этим в области 1-Н произошло увеличение плотности газа на величину
(давление за фронтом сжатия). В соответствии с этим в области 1-Н произошло увеличение плотности газа на величину
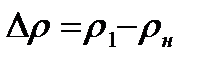
Увеличение плотности возможно только благодаря увеличению массы газа в указанной области 1-Н на величину
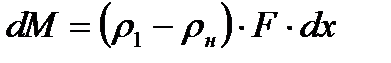 (8.1)
(8.1)
Увеличение массы произошло вследствие перетока газа из объема 0-1 в объем 1-Н со скоростью 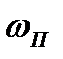 . Эту массу газа
. Эту массу газа 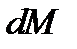 можно вычислить через
можно вычислить через 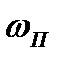 как
как
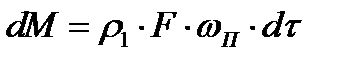 (8.2)
(8.2)
Тогда, приравнивая выражения (8.1) и (8.2), получим
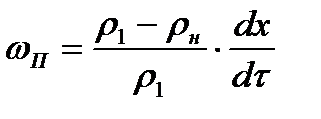 (8.3)
(8.3)
Выражение 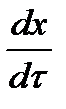 представляет собой скорость движения волны
представляет собой скорость движения волны 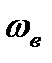 , т.е.
, т.е.
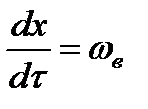 (8.4)
(8.4)
Тогда равенство (8.3) примет вид
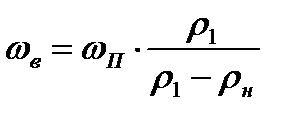 (8.5)
(8.5)
которое связывает скорость распространения волны со скоростью газа, движущегося за фронтом волны в том же самом направлении.
Выразим скорость распространения волны только через параметры 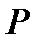 и
и 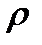 в возмущенной (с индексом 1) и невозмущенной областях (с индексом Н). Для этого воспользуемся уравнением изменения количества движения для массы
в возмущенной (с индексом 1) и невозмущенной областях (с индексом Н). Для этого воспользуемся уравнением изменения количества движения для массы 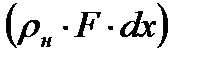 газа в объеме 1-Н, находящейся в покое в момент времени
газа в объеме 1-Н, находящейся в покое в момент времени 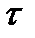 . За время
. За время 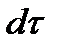 эта масса приходит в движение со скоростью
эта масса приходит в движение со скоростью 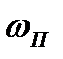 .
.
Изменение количества движения рассматриваемой массы газа должно быть равно импульсу силы, вызванной разностью давлений в сечениях 1-1 и Н-Н. В проекции на ось потока это уравнение имеет вид
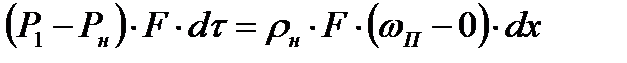 ,
,
отсюда с учетом (8.4) имеем
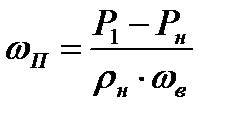 (8.6)
(8.6)
Подставляя значение 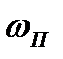 по формуле (8.6) в выражение (8.5), получим
по формуле (8.6) в выражение (8.5), получим
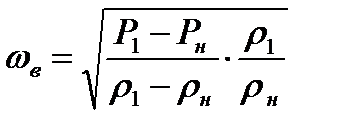 (8.7)
(8.7)
В случае слабой волны возмущения, повышение давления и плотности незначительно, т.е. 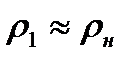 и
и 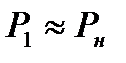 . Приходя к пределу в (8.7) при
. Приходя к пределу в (8.7) при 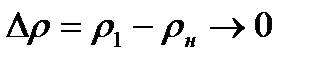 , получим скорость распространения малых возмущений, т.е. скорость акустической волны (или скорость звука)
, получим скорость распространения малых возмущений, т.е. скорость акустической волны (или скорость звука)
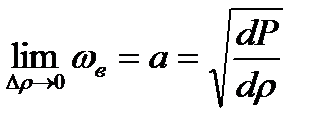 ( 8.8)
( 8.8)
Подставляя (8.7) в (8.5), получим выражение для скорости газового потока за фронтом волны сжатия
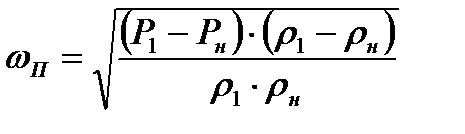 (8.9)
(8.9)
Прямой скачок уплотнения
 Рассмотрим случай, когда фронт сильной волны составляет прямой угол с направлением движения газа. Такая волна называется прямой ударной или прямым скачком уплотнения (рис. 8.2)
Рассмотрим случай, когда фронт сильной волны составляет прямой угол с направлением движения газа. Такая волна называется прямой ударной или прямым скачком уплотнения (рис. 8.2)
Рис. 8.2. Схема прямого скачка уплотнения
Найдем соотношения, связывающие параметры состояния газа перед и за фронтом ударной волны. Рассмотрим схему, когда фронт волны неподвижен. Если же в действительности ударная волна движется, то можно перейти к рассмотрению указанной схемы путем обращения движения. Т.е. остановим фронт волны, направив поток газа навстречу волне со скоростью, равной скорости распространения волны 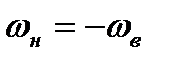 . Это равносильно тому, что вводится в рассмотрение система координат, жестко связанная с ударной волной, т.е. система координат движется со скоростью
. Это равносильно тому, что вводится в рассмотрение система координат, жестко связанная с ударной волной, т.е. система координат движется со скоростью 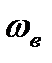 . Тогда газ будет перемещаться относительно этой системы координат со скоростью
. Тогда газ будет перемещаться относительно этой системы координат со скоростью 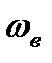 перед фронтом волны и за фронтом волны со скоростью
перед фронтом волны и за фронтом волны со скоростью
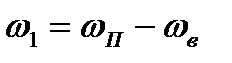 (8.6)
(8.6)
Таким образом, в выбранной системе координат имеется неподвижная поверхность (ударная волна), которую пересекает газ. При этом параметры потока таза: скорость движения, плотность, давление и температура - претерпевает скачкообразное изменение. Именно поэтому ударную волну называют еще скачком уплотнения.
Визуально скачки уплотнения можно наблюдать в сверхзвуковых аэродинамических трубах при обтекании воздухом неподвижных твердых тел.
Для отыскания связи параметров потока по обе стороны скачка уплотнения воспользуемся уравнением неразрывности, которое для случая 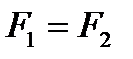 принимает вид
принимает вид
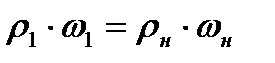 (8.7)
(8.7)
и уравнением изменения количества движения
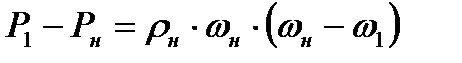 (8.8)
(8.8)
Равенство (8.8) можно преобразовать
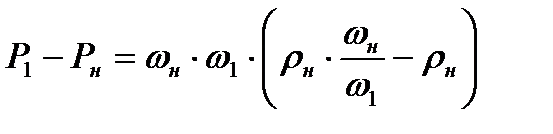
Подставляя сюда выражение 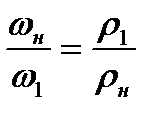 , найденное из (8.7), получим
, найденное из (8.7), получим
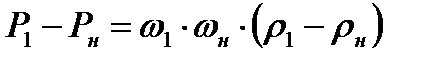 (8.9)
(8.9)
или
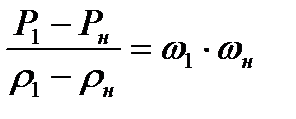 (8.10)
(8.10)
Найдем соотношение, связывающее скорость газа по обе стороны скачка уплотнения со скоростью звука. Для этого воспользуемся уравнением Бернулли-Сен-Венана для двух сечений, расположенных на бесконечно близком расстоянии друг от друга: одно сечение выбрано но одну сторону скачка уплотнения (в невозмущенной области), другое - за скачком уплотнения
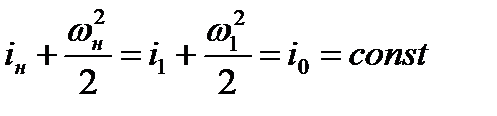 (8.11)
(8.11)
Правомерность использования этого уравнения вытекает из того, что боковая поверхность отсека потока 1-Н (т.е. в области скачка) ничтожна мала, энергообменом через эту поверхность можно пренебречь.
Согласно (1.18) можно записать
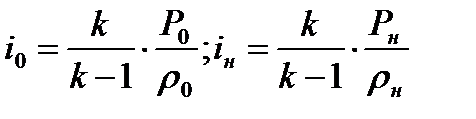 (8.12)
(8.12)
Подставляя эти значения энтальпии в (8.11) и решая уравнение относительно 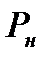 , получим
, получим
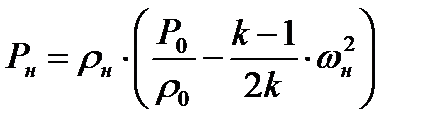 (8.13)
(8.13)
По аналогии из (8.11), с учетом (8.12), можно получить равенство
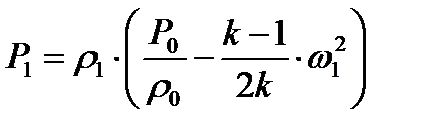 (8.14)
(8.14)
Вычитая почленно равенство (8.13) из (8.14), имеем
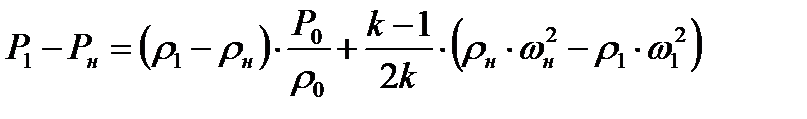 (8.15)
(8.15)
Используя соотношение (8.7), преобразуем равенство (8.8) к виду
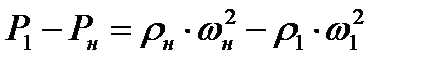 (8.16)
(8.16)
Подставляя (8.16) в (8.15), после несложных выкладок можно получить
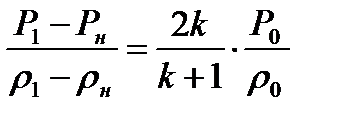 (8.17)
(8.17)
Воспользуемся выражением (3.10), которое с учетом уравнения Клапейрона-Менделеева (1.3) примет вид
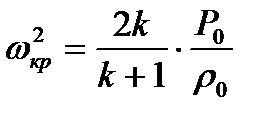 (8.18)
(8.18)
Используя последнее равенство, могло выражение (8.17) представить к виду
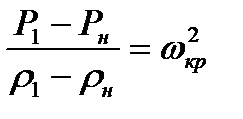 (8.19)
(8.19)
Сопоставляя равенства (8.10) и (8.19), можно получить искомое соотношение, связывающее скорости потока газа перед и за скачком уплотнения с критической скоростью.
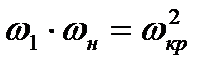 (8.20)
(8.20)
Последнее соотношение называется формулой Прандтля. Его можно представить еще иначе, если заменить в нем скорости 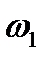 и
и 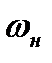 через соответствующие значения коэффициента скорости
через соответствующие значения коэффициента скорости 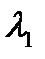 и
и 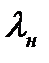
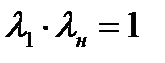 (8.21)
(8.21)
Соотношения (8.20) и (8.21) позволяют сделать важный вывод. В прямом скачке уплотнения всегда сверхзвуковая скорость газа переходит в дозвуковую, так как если 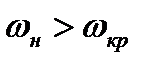 , то
, то 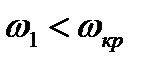
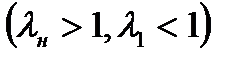 . Более того, чем выше значение безразмерной скорости
. Более того, чем выше значение безразмерной скорости 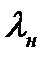 (следовательно и
(следовательно и 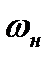 ), тем меньше ее значение после скачка. Иными словами, чем выше начальная скорость сверхзвукового потока, тем сильнее получается скачок уплотнения. С уменьшением начальной скорости скачок ослабевает и исчезает совсем, при
), тем меньше ее значение после скачка. Иными словами, чем выше начальная скорость сверхзвукового потока, тем сильнее получается скачок уплотнения. С уменьшением начальной скорости скачок ослабевает и исчезает совсем, при 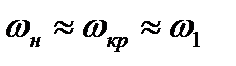 Тем самым доказывается, что ударные волны возможны только при сверхзвуковых течениях газа. Этот вывод подтверждается и экспериментально.
Тем самым доказывается, что ударные волны возможны только при сверхзвуковых течениях газа. Этот вывод подтверждается и экспериментально.
Установим теперь связь между давлением и плотностью газа в скачке уплотнения. Для этого используя выражение (8.13) и (8.14) и исключая из них скорости 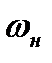 и
и 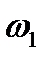 , с учетом (8.9) можно получить (выкладки опускаются)
, с учетом (8.9) можно получить (выкладки опускаются)
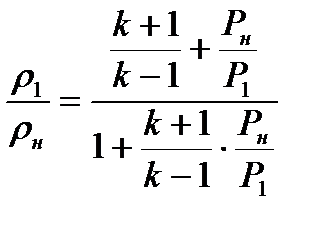 (8.22)
(8.22)
Соотношение (8.22) позволяет судить о термодинамическом процессе изменения состояния газа в скачке уплотнения и называется ударной адиабатой или адиабатой Гюгонио.
Следует подчеркнуть, что при прохождении газа через скачок уплотнения уравнение адиабаты Пуассона (1.21) теряет силу, т.е. процесс движения газа становится неизоэн- тропийным. Вместо (1.21) должно использоваться уравнение ударной адиабаты (8.22).
Из (8.22) видно, что при неограниченном возрастании давления в скачке уплотнения 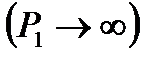 увеличение плотности имеет определенный предел
увеличение плотности имеет определенный предел
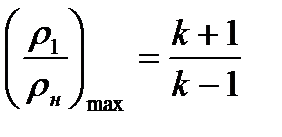 (8.23)
(8.23)
Например, для воздуха ( 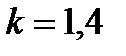 ) увеличение плотности в скачке уплотнения может быть не более чем в 6 раз (
) увеличение плотности в скачке уплотнения может быть не более чем в 6 раз ( 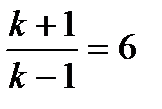 ). Если бы процесс оставался адиабатическим (при прохождении скачка уплотнения), то увеличение плотности с ростом давления было бы неограниченным. Это следует из выражения
). Если бы процесс оставался адиабатическим (при прохождении скачка уплотнения), то увеличение плотности с ростом давления было бы неограниченным. Это следует из выражения
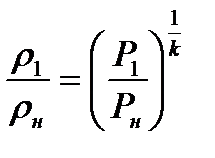 (8.24)
(8.24)
которое получается при формальном использовании уравнения (1.21).
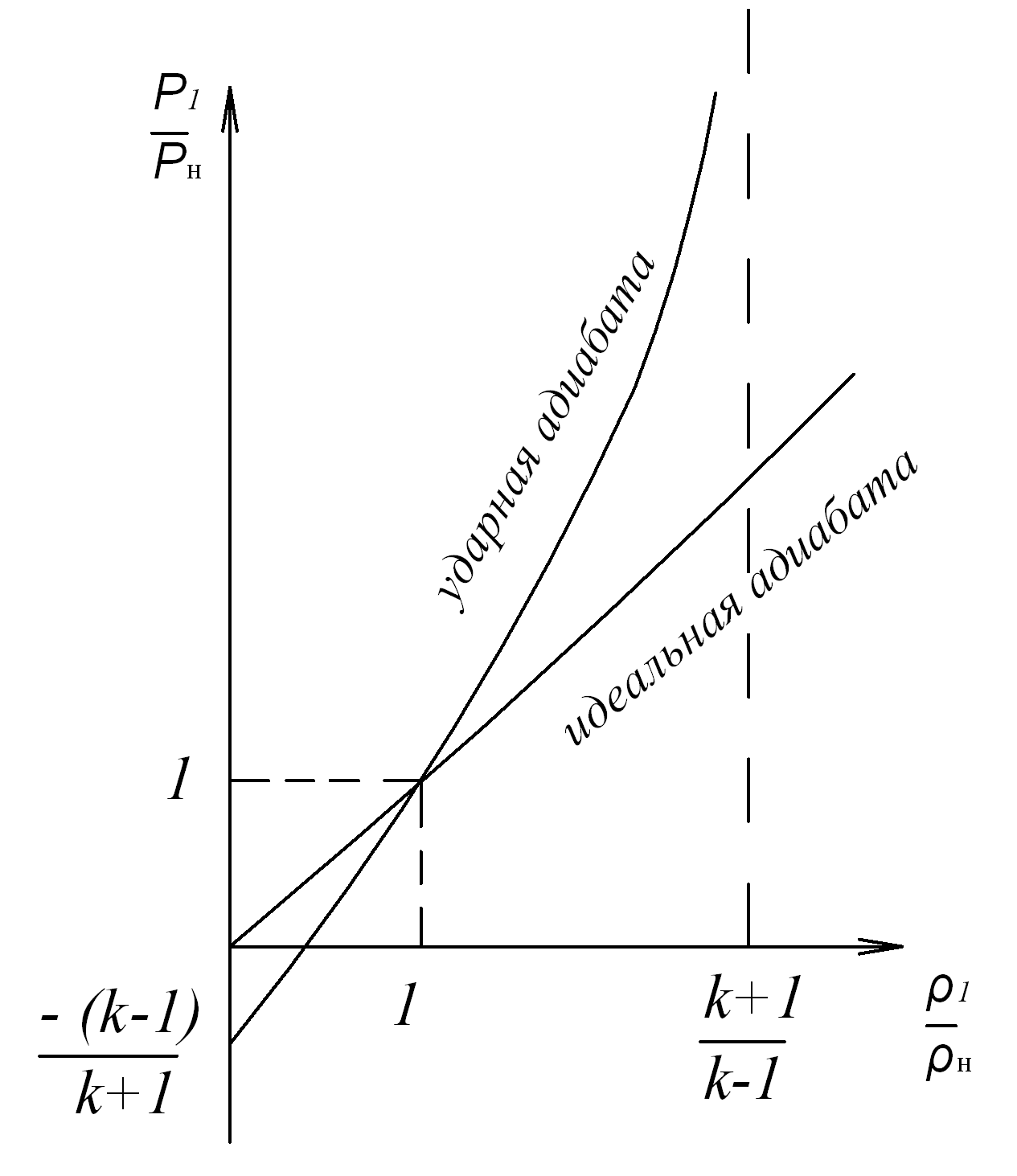 Графическое представление зависимостей (8.22) и (8.24) дается на рис. 8.3
Графическое представление зависимостей (8.22) и (8.24) дается на рис. 8.3
Рис. 8.3. Графическое представление ударной (Гюгонио) и идеальной (Пуассона) адиабат
Выражение (8.22) иногда удобнее использовать в другом
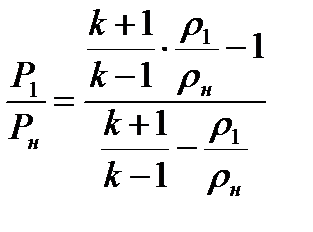 (8.25)
(8.25)
Можно выразить отношение давлений в прямом скачке уплотнения и в функции коэффициента скорости перед скачком уплотнения 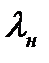
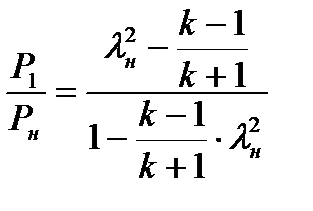 (8.26)
(8.26)
которое получается из (8.25) исключением плотности.
Выражения (8.25) и (8.26) позволяют определять потери полного давления в прямом скачке уплотнения.
Косой скачок уплотнения
Характерной особенностью прямого скачка является то, что, пересекая его фронт, газовый поток не меняет своего направления.
Скачок, фронт которого расположен наклонно к направлению потока, называется косым. Такой скачок получается в случае обтеканий сверхзвуковым потоком профилированных тел. При нерасчетном режиме истечения из сопла Лаваля внутри него иногда образуется сложная система косых скачков уплотнения. При прохождении косого скачка уплотнения газовый поток меняет свое направление. Для установления закономерностей рассмотрим сверхзвуковое обтекание клина (рис. 8.4). С острия клина сходят два плоских 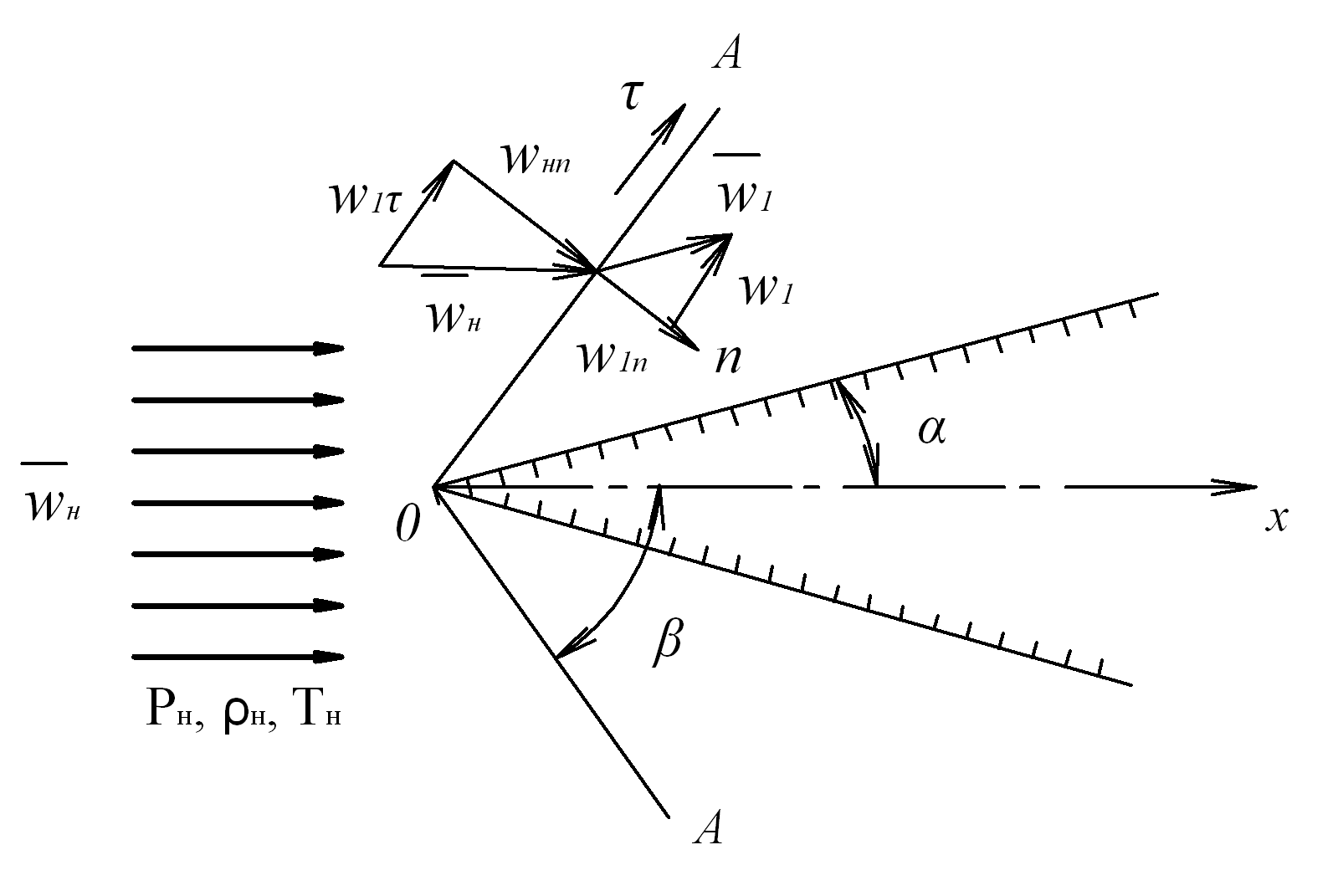 косых скачка уплотнения OA, образующих со скоростью
косых скачка уплотнения OA, образующих со скоростью  угол
угол 
Рис. 8.4. К выводу основных расчетных соотношений для косого скачка уплотнения
Массовый расход газа через единицу площади поверхности фронта OA определяется нормальной составляющей скорости
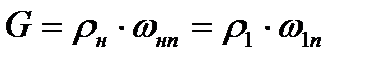 (8.27)
(8.27)
Закон изменения количества движения в векторной форме запишется в виде
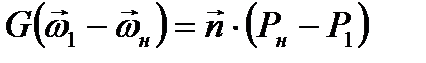 (8.28)
(8.28)
где 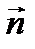 - единичный вектор нормали к поверхности скачка.
- единичный вектор нормали к поверхности скачка.
Проекция уравнения (8.28) на плоскость OA дает соотношение
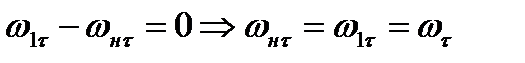 (8.29)
(8.29)
которое позволяет сделать важный вывод: при пересечении скачка уплотнения касательная составляющая скорости не терпит разрыва.
Уравнение (8.28) в проекции на направление 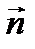 имеет вид
имеет вид
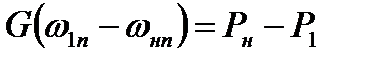 (8.30)
(8.30)
из которого следует, что нормальная составляющая скорости потока терпит разрыв (т.к. 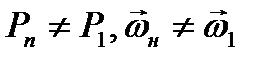 , в противном случае скачка нет).
, в противном случае скачка нет).
Так же как и в случае прямого скачка воспользуемся уравнением энергии в форме (8.11). Подставляя в него выражение энтальпии по формуле (8.12) и значения скоростей
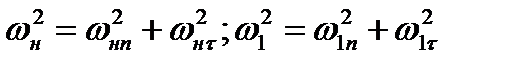
получим, с учетом соотношения (8.29)
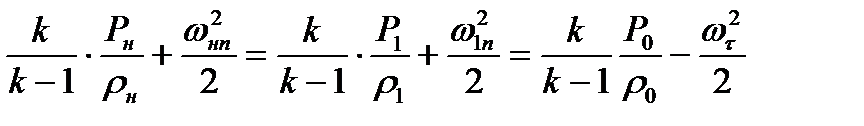 (8.31)
(8.31)
Сравнивая между собой уравнения (8.27), (8.30) и (8.31) для косого скачка с соответствующими уравнениями (8.7), (8.8) и (8.11) для прямого скачка, видим, что указанные системы уравнений совпадают между собой, если в уравнениях для прямого скачка заменить скорости 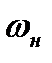 и
и 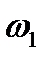 на
на 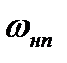 и
и 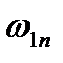 , а величину
, а величину 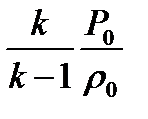 на
на 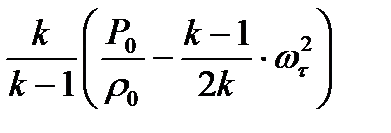 (8.32)
(8.32)
Следовательно, все формулы, полученные для прямого скачка, остаются в силе, если в них произвести указанную замену. Это равносильно тому, что косой скачок уплотнения сводится к прямому скачку, который сносится вместе с потоком газа по касательной 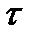 со скоростью
со скоростью 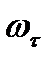 .
.
Адиабата Гюгонио (8.22) полностью сохраняется и для косого скачка уплотнения, т.к. в ней не содержится скорости. Формула Прандтля (8.20) с учетом (8.18) и замены (8.32) для случая косого скачка уплотнения принимает вид
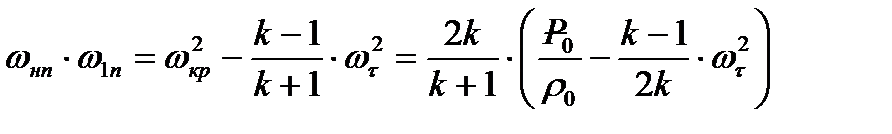 (8.33)
(8.33)
Из формулы (8.33) следует вывод: в случае косого скачка уплотнения всегда 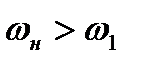 , причем могут реализовываться случаи, когда
, причем могут реализовываться случаи, когда 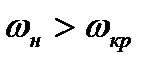 и
и 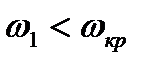 т.к. в отличие от прямого скачка, скорость за косым скачком уплотнения может оставаться сверхзвуковой.
т.к. в отличие от прямого скачка, скорость за косым скачком уплотнения может оставаться сверхзвуковой.
Для косого скачка можно получить соотношение, позволяющее оценить интенсивность изменения давления в зависимости от угла 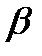
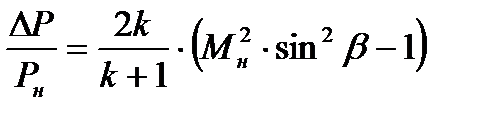 (8.34)
(8.34)
где 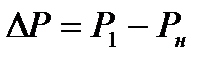
9. ОСНОВНЫЕ ЗАДАЧИ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ГАЗА В ТРУБАХ
Неотъемлемой частью проектирования любого газопровода является газодинамический расчет его линейной части. Этот расчет базируется на закономерностях движения газа в трубах постоянного диаметра, которые и будут рассмотрены ниже. При этом принимается, что движение дозвуковое. Это отвечает реальным условием, т.к. скорость движения газа в линейной части газопровода меньше скорости звука и резко превосходят 50-60 м/с, а числа Маха соответственно значительно меньше единицы. Звуковые скорости могут возникать только в отдельных узлах арматуры (в регуляторах давления и расхода, задвижках и т.п.).
