Относительное движение материальной точки

В предыдущем параграфе показано было как определяется движение точки относительно неподвижной системы отсчета, абсолютное движение. Нередко приходится исследовать движение материальной точки относительно системы, которая сама движется и довольно сложным образом.

Точка М (рис.26) под действием некоторых сил совершает сложное движение. Абсолютное определяется координа­тами x, y, z, относительное – координа­тами x₁, y₁, z₁.

Рис.26

Составим основное уравнение динамики для точки 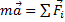, где абсолютное ускорение . Поэтому уравнение будет таким или .

Рис. 13.6.

Но - переносная сила инерции, - кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так

Спроектировав это векторное равенство на подвижные оси x₁, y₁, z₁, имея в виду, что проекции вектора ускорения на оси – есть вторые производные от соответствующих координат по времени, получим дифференциальные уравнения относительного движения

Сравнивая эти уравнения с дифференциальными уравнениями абсолютного движения, замечаем, что относительное движение материальной точки определяется такими же методами, что и абсолютное, надо лишь кроме обычных сил учесть переносную силу инерции и кориолисову силу инерции.

Если переносное движение поступательное, равномерное и прямолинейное, т.е. подвижная система инерциальная, то ускорение и . Значит и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).

Поэтому невозможно установить, наблюдая за движением точки, движется система поступательно, равномерно и прямолинейно или находится в покое. Этот вывод впервые был сделан Г.Галилеем и называется его именем – принцип относительности Галилея.

Физические величины и физические законы, не изменяющиеся при переходе от одной инерциальной системы отсчета к другой, называют инвариантными (не изменяющимися) к преобразованиям Галилея.

Пример 26. Вагон движется с постоянным ускорением 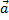. Определим траекторию движения предмета М, упавшего с полки высотой h, которую увидит наблюдатель, пассажир, сидящий в вагоне (рис.27).

Рис. 13.7.

Рис.27

Порядок решения задачи тот же, что и при определении абсолютного движения. Только оси надо провести по вагону и учесть кроме веса предмета 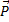переносную силу инерции (кориолисова сила инерции – переносное движение поступательное).

Дифференциальные уравнения относительного движения получаются такими

Решение этих уравнений

.

Используя начальные условия (при t = 0: x₁ = 0, y₁ = h, т.к. ), найдем постоянные интегрирования: C₁=C₂=D₁=0, D₂=h. Поэтому уравнения движения: Траекторию движения получим, исключив параметр t: Это уравнение прямой (рис. 27). Предмет М упадет на пол вагона на расстоянии от края полки (при ).

Если вагон будет двигаться равномерно (W = 0), то s = 0. Наблюдатель увидит траекторию – вертикальную прямую, такую же, как и при неподвижном вагоне.

Пример 27. Внутри трубки, вращающейся с постоянной угловой скоростью 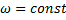вокруг вертикальной оси, находится шарик М, привязанный нитью длиной а к оси вращения (рис. 28). Определим движение шарика в трубке после того, как нить оборвется. Сопротивление воздуха учитывать не будем.

Рис. 13.8.

Рис.28

Траектория движения шарика в трубке – прямая. Поэтому для определения этого движения достаточно одной координаты х₁. Начало координат, точка О, - на оси вращения. В промежуточном положении на шарик действуют силы: вес 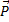, две составляющие реакции трубки . Добавляем переносную силу инерции кориолисову силу инерции и составляем дифференциальное уравнение движения: . Или, после подстановки значения силы инерции и преобразований: .

Решение такого дифференциального уравнения, как известно, имеет вид: и .

Так как при t = 0 x₁ = 0, , то С₁ +С₂ = а, С₁ – С₂ = 0.

Значит C₁=C₂=a/2 и уравнение движения станет таким

Относительная скорость . А т.к. , то

Можно теперь определить относительную скорость шарика в любом положении. Так шарик вылетит из трубки длиной l со скоростью