Дәріс тақырыбы: Үш өлшемді евклидтік кеңістігі үшін Вейль аксиомаларының қайшылықсыздығы мен толықтығы

Жоспары

1. Үш өлшемді евклидтік кеңістікке арналған Вейль аксиомалары
2. Вейль аксиомалары системасының қайшылықсыздығы мен толықтығы

Дәріс тезисі.

1. Үш өлшемді нақты евклидтік 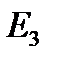кеңістік структурасының анықтамасын еске түсірейік.

V кеңістігі –нақты сандардың R өрісі үстіндегі үщ лшемді векторлық кеңістік болсын. Егер Вейльдің төмендегі үш аксиомасын қанағаттандыратын 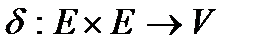бейнелеуі берілсе, 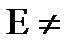◙ жиыны 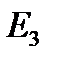кеңістік деп аталады., ол аксиомалар мыналар:

1) әрбір 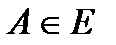элементі үшін 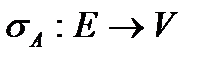бейнелеуі

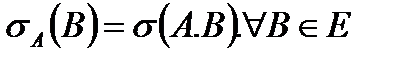
Заңы бойынша биекция болып табылады.

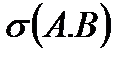векторын әдетте 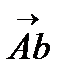деп белгілейді. Осы 1-аксиома бойынша

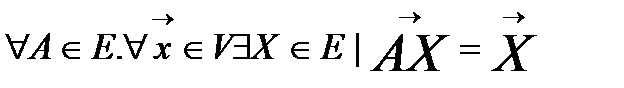
Болады және мұндай 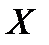элементі біреу ғана болады.

2)

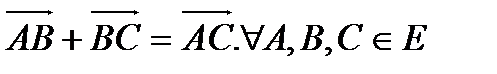
3) 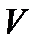векторлық кеңістікгі үстінде оң таңбалы

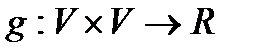
Бисызықтық форма берілді деген сөз( мұндағы 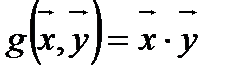санын 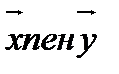векторларыныңи скаляр көбейтіндісі деп атайды

1-2 аксиомалар үщ өлшемді нақты Аффиндік А₃ кеңістігінің структурасын анықтайды.

Сонымен, евклидтік 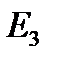кеңістігі структурасының базасы E,V,R жиындарының үштігі болады, мұндағы R –нақты сандардың өрісі, ал V жиыннның үлсіне R үстіндегі үщ өлшемді евклидтік векторрлық кеңістіктің струтурасы тиген. 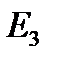структурасын анықтауда Е жиыны- негізіг жиын рөлін, VменR жиындары – көмекші жиындар рөльдерін атқарады, атап айтқанда R өрісі векторлық кеістіктің аксиомалары бойынша V үстінде қолданылатын операторлардың жиыны, ал V жиыны Вейльдың 1-3 аксиомалары бойынша Е жиыны үстінде қолданылатын операторлардың жиыны болады.

2. Кітаптың екінші бөлімінде кез келген п натурал сан үшін Е евклидтік кеңістік болатындығы дәлелденген. Онда Е жиыны ретінде 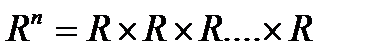п рет жиыны алынған.

3. Теорема. Егер нақты сандардың арифметикасы қайшылықсыз болса, онда 1-3 Вейль акстомаларының системасы қайшылықсз болады.

Аксиомалардың бұл системасының толымдылық қасиеті де бар, өйткені оның интерпретацияларының бәрі изоморфты болып отырады.

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:

Дәріс тақырыбы: Түзулердің, жазықтықтардың, кесінділердің, сәулелердің, бұрыштардың анықталуы

Жоспары:

1. Түзулердің, жазықтықтардың анықталуы
2. Кесінділердің, сәулелердің, бұрыштардың анықталуы

Дәріс тезисі.

Осы параграфтың атымен аталынған фигуралардың 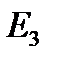кеңістігіндегі анықтамаларын еске түсірейік ( 1 бөлімнің 2 бөліміндегі IV тарауды қараңыз)

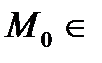
1. 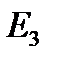нүктесі мен 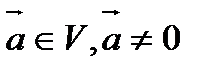векторын алайық ( мұндағы V жиыны 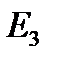кеңістігінің көшірулер кеңістігі) d түзуі M нүктелерінің жиыны ретінде анықталады:

(*)

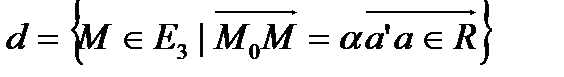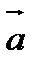векторы – d түзуінің бағыттаушы векторы. Егер 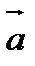векторына коллинеар 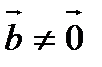векторы алынса, онда 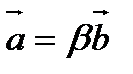және 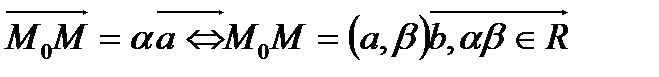сондықтан 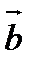векторы да түзуінің бағыттаушы векторры болады.

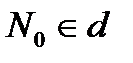нүктесін алайық. Сонда

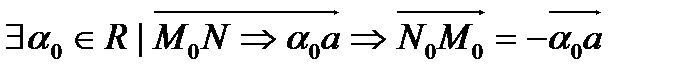(1)

Болады. Сонымен қатар 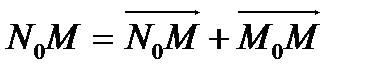(2)

Болатыны мәлім.

(1), (*) (2) 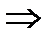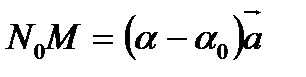мұндағы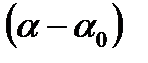

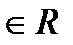
Демек 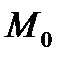нүктесі d түзуінің анықтамасында айтарлықтай айрықша роль атқармайды, оны сол түзудің кез келген 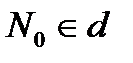нүктесімен ауыстыруға болады.

2. Колленеар емес 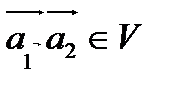векторлары мен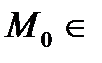 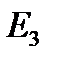нүктесін алайық. М нүктелерінің мынадай II жиынын біз жазықтықдеп атаймыз.

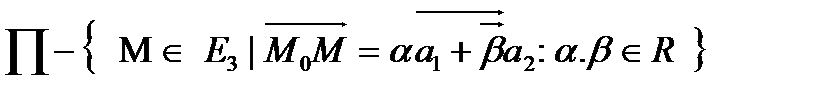
Бұл анықтамада да нүктесін кез келген 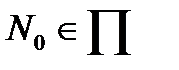нүктесімен ауыстыруға болады. Айта берсек 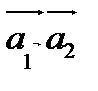векторларының орнына сол 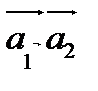векторлары арқылы өтетін екі өлшемді 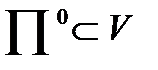векторлық бөлімше кеңістіктің кез келегн басқа бір базисін алғанда да П жиыны бұрыңғы қалпында қалады. Бұл 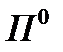бөлімше кеңістігі П жазықтығының бағыттайтын бөлімше кеңістігі немесе бағыттаушысы деп аталады. Бір түзудің бойында жатпайтын үш нүкте A.B.C 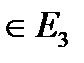өздерінен өтетін (A.B.C) жазықтығын анықтайды:

(A.B.C)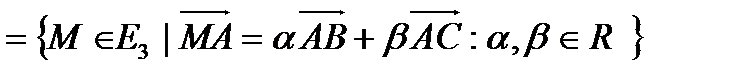

Егер (А,В) түзуінің әр түрлі екі нүктесі П жазықтыығында жатса, онда ол түзудің әрбір нүктесі де П жазықтығында жатады. Мұндай жағдайда (А,В) түзуі П жазықтығында жатады делінеді де былай жазылады: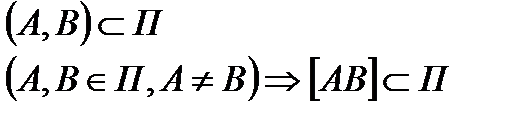

Болатыныдығы түсінікті.

П жазықтығында жататын d түзуін алаық және 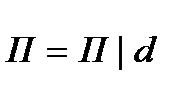болсын.

П жазықтығында 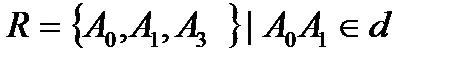(139 сурет) координаталар системасы берілсін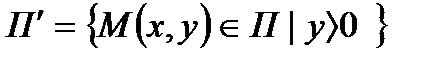 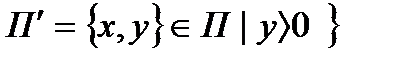фигуралары қарастырылды. Яғни мұнда

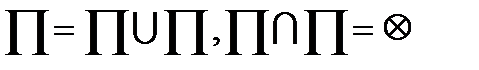
А2

Аа

А1

d

П\\

(139- сурет)

П жазықтығында. Бас нүктесі ортақ, (ОА) және (ОВ) сәулелері берілсін

( 140- сурет). Алдымен осы сәулелердің бір түзудің бойында жатпайтын жағдайын қарастырайық. Онда П жазықтығында жататын төмендегідей фигураларды қарастырайық:

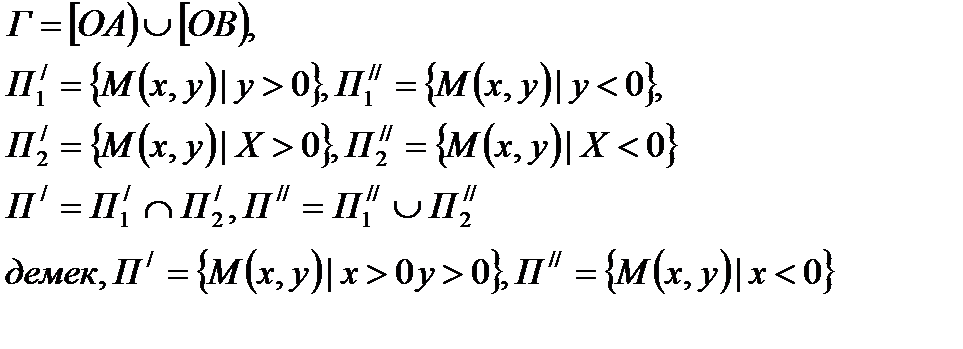болатыны айқын

Егер 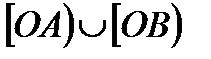=Г түзу сызық болса, онда түзу П Г фигурасын П^/және П^{// бөлікке бөледі (141- сурет)}. Онда әрбір Е^/= П^/U Г , Е^//= П^//U Г фигуралары, төбесі О нүктесі, қабырғалары [ОА) және [ОВ) сәулелері болатын жазық бұрыш деп аталады, ал П^/

Фигурасы Е^/ бұрыштың ішкі облысы деп аталады.

Сонымен, жазық бұрыш дегеніміз- шекарасында бұрыштың О төбесі көрсетілген жарты жазықтық.

^/

В

О

А

Г

П/

П//

(141 сурет)

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с: