Методы определяющих координат
В основе любого метода расчета электрических цепей лежат фундаментальные законы теории цепей — законы Кирхгофа и Ома. Однако непосредственное использование данных законов для расчета токов и напряжений, как уже отмечалось выше, требует решения системы уравнений порядка 2b, где b — число ветвей в анализируемой цепи.
На практике для описания электрических цепей используют методы определяющих координат, согласно которым из всех токов и напряжений ветвей выбирается некоторая минимальная в каком-то смысле совокупность токов и (или) напряжений ( определяющих координат ), относительно которых формируются и решаются уравнения цепи, после чего оставшиеся токи и напряжение ветвей определяются по достаточно простым соотношениям. Очевидно, совокупность определяющих координат должна полностью характеризовать поведение электрической цепи. Если в определяющие координаты включены только токи или только напряжения, то такой координатный базис называется однородным, в противном случае — неоднородным или смешенным. Уравнения в однородном базисе формируются сравнительно просто.
В качестве координат, относительно которых записываются уравнения, часто рассматриваются сечения и контуры. Каждому сечению можно поставить в соответствие напряжение ребра графа (узловое напряжение), а каждому контуру — ток хорды (контурный ток). Упорядоченная совокупность напряжений ребер образует вектор узловых напряжений U ,а совокупность токов хорд — вектор контурных токов I. Размерность первого вектора равна n-1 , второго –– b-n+1.
Поскольку каждая ветвь графа образует с ребрами замкнутый контур, то напряжения ветвей можно выразить по второму закону Кирхгофа через узловые напряжения. Совокупность ветвей дерева, образующих с некоторой ветвью графа контур, определяется совокупностью инцидентных данной ветви сечений. Последняя, в свою очередь, определяется ненулевыми элементами столбца матрицы сечений, соответствующего данной ветви. Следовательно
 (2. 32)
(2. 32)
или
 . (2. 33)
. (2. 33)
Последние соотношения совместно с (1. 13) можно рассматривать как три эквивалентных формы записи второго закона Кирхгофа, Поскольку они устанавливают равновесия напряжений ветвей.
Ток любой ветви равен алгебраической сумме токов контуров, инцидентных рассматриваемой ветви. Совокупность контуров, инцидентных некоторой ветви, определяется ненулевыми элементами соответствующего столбца матрицы Р . Это позволяет записать уравнения равновесия токов в следующей форме
 , (2. 34)
, (2. 34)
которая совместно с соотношениями (1. 10) и (1. 11) представляет три матричные форма записи первого закона Кирхгофа.
Уравнения электрических цепей, составленные относительно контурных токов, можно получить используя следующие формы законов Ома и Кирхгофа:
- закон Ома 
- первый закон Кирхгофа 
- второй закон Кирхгофа 
Сведем последние уравнения в единое матричное уравнение вида
 , (2. 35)
, (2. 35)
в котором 1 и 0 обозначают, соответственно, единичную и нулевую матрицы.
Дальнейшие преобразования уравнений (2. 35) связаны с исключением из его третьей строки переменных  и
и  . Для исключения переменной воспользуемся первой строкой уравнения (2. 35), для чего умножим ее на
. Для исключения переменной воспользуемся первой строкой уравнения (2. 35), для чего умножим ее на  матрицу Р и результат вычтем из третьей строки. Получаем уравнение
матрицу Р и результат вычтем из третьей строки. Получаем уравнение

 .
.
Используя вторую строку, исключаем аналогичным образом переменную 
 (2. 36)
(2. 36)
Последняя строка и соответствует уравнениям контурных токов
 .
.
Определяя матрицу сопротивления  и вектор задающих (контурных) напряжений
и вектор задающих (контурных) напряжений  , уравнение контурных токов запишем как
, уравнение контурных токов запишем как  .
.
Решив данную систему уравнений 
 , искомые токи и напряжения ветвей определяются подстановкой вектора I в первую и вторую строки уравнения (2. 36) :
, искомые токи и напряжения ветвей определяются подстановкой вектора I в первую и вторую строки уравнения (2. 36) :

 .
.
МЕТОД КОНТУРНЫХ ТОКОВ.Уравнения контурных токов могут быть сформированы и без использования топологических матриц. Наиболее просто это выполняется в случае, если рассчитываемая электрическая цепь может быть представлена без пересечения ветвей. Рассмотрим электрическую схему, приведенную на рисунке 2. 21.

Рисунок 2. 21
Выбрав каноническую систему контуров и приняв одинаковую ориентацию для всех контуров (по часовой стрелке, как это представлено на рисунке, либо против часовой стрелки), систему контурных уравнений можно представить в следующем виде

 (2. 37)
(2. 37)

где

- собственные сопротивления контуров (сумма сопротивлений ветвей, образующих контур);

- взаимные сопротивления контуров (сумма сопротивлений общих для двух контуров, взятая со знаком минус);

- контурные ЭДС (алгебраическая сумма ЭДС ветвей, образующих контур, в которую источник входит со знаком плюс, если его ориентация совпадает с направлением обхода контура, и со знаком минус - в противном случае).
Для получения узловых уравнений сведем в единое матричное уравнение законы Ома и Кирхгофа, представленные в формах (1. 8), (2. 33) и (1. 10) :
 .
.
Исключая из третьей строки переменную  , а затем и
, а затем и  , находим
, находим
 . (2.38)
. (2.38)
Третья строка соотношения (2.38) представляет уравнения узловых напряжений, записанные в матричной форме  ,
,
 где
где  — матрица проводимостей;
— матрица проводимостей;

 –– вектор задающих токов узлов.
–– вектор задающих токов узлов.
Решив узловые уравнения 
токи и напряжения ветвей рассчитываются с помощью первых двух уравнений из (2. 38) :

 .
.
Рассмотрим другой, более наглядный, подход к решению системы уравнений (2. 37). Представим эту систему в матричной форме следующего вида:
 . (2. 39)
. (2. 39)
В этом уравнении [ 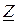 ] — матрица сопротивлений;
] — матрица сопротивлений;  — матрица-столбец контурных токов;
— матрица-столбец контурных токов;  –– матрица-столбец контурных ЭДС. Эти матрицы имеют следующий вид :
–– матрица-столбец контурных ЭДС. Эти матрицы имеют следующий вид :

 .
.
Систему уравнений (2. 37) или (2. 39) можно решить различными методами, например, методом Крамера. Ток k- го контура можно представить в общем виде следующим выражением :
 , (2. 40)
, (2. 40)
где  –– определитель системы уравнений;
–– определитель системы уравнений;  –– алгебраические дополнения соответствующих элементов. Для линейных цепей справедливо равенство
–– алгебраические дополнения соответствующих элементов. Для линейных цепей справедливо равенство  . Матрицу сопротивления можно записать по заданной схеме при условии, что направления контурных токов выбрано одинаковым. Для этого составляется таблица
. Матрицу сопротивления можно записать по заданной схеме при условии, что направления контурных токов выбрано одинаковым. Для этого составляется таблица  , где n-число контуров. В клетки, расположенные по главной диагонали помещают собственные сопротивления контуров, в остальные клетки - взаимные сопротивления контуров, то есть, взятые со знаком ‘‘ минус ’’ сопротивления общих элементов контуров. Так, матрица сопротивлений для схемы рисунка 2. 21 имеет вид :
, где n-число контуров. В клетки, расположенные по главной диагонали помещают собственные сопротивления контуров, в остальные клетки - взаимные сопротивления контуров, то есть, взятые со знаком ‘‘ минус ’’ сопротивления общих элементов контуров. Так, матрица сопротивлений для схемы рисунка 2. 21 имеет вид :
 |  |  | |
[ 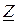 ] = 2 ] = 2 |  |  |  |
 |  |  |
Если какие-либо два контура не имеют общего элемента, то в соответствующую клетку в таблице записывается ноль.
МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ.Как и в случае метода контурных токов, коэффициентная матрица (матрица проводимостей) и вектор правых частей узловых уравнений могут быть рассчитаны без использования топологических матриц. Обратимся еще раз к анализу схемы, приведенной на рисунке 2. 21. Заземлим один из узлов этой схемы и пронумеруем оставшиеся. Выбор “заземленного” (базисного) узла является произвольным, однако удобнее всего в качестве базисного выбирать узел, к которому подключено максимальное число ветвей.
Составим узловые уравнения для узлов 1, 2, 3 по первому закону Кирхгофа :

Выразим токи ветвей по закону Ома в комплексной форме :


После подстановки этих формул в узловые уравнения и выполнения ряда преобразований получим систему уравнений :
 ; (2. 41)
; (2. 41)
 ;
;
 .
.
Величины 
представляют собой суммы проводимостей всех ветвей, подключенных к данному узлу. Называются они собственными проводимостями узлов. Величины  называются взаимными проводимостями узлов. Алгебраическая сумма постоянных величин, имеющих размерность тока, в правой части уравнений (2. 41) называются задающими токами узлов :
называются взаимными проводимостями узлов. Алгебраическая сумма постоянных величин, имеющих размерность тока, в правой части уравнений (2. 41) называются задающими токами узлов :


Заметим, что если ЭДС направлена к узлу, то соответствующее произведение  берется со знаком “плюс” . С учетом введенных обозначений уравнения (2. 41) можно записать в каноническом виде :
берется со знаком “плюс” . С учетом введенных обозначений уравнения (2. 41) можно записать в каноническом виде :

 (2. 42)
(2. 42)

или в матричной форме

где  –– матрица проводимостей.
–– матрица проводимостей.
Общее решение уравнений (2. 42) имеет вид :
 , (2. 43)
, (2. 43)
где  –– определитель матрицы проводимостей ;
–– определитель матрицы проводимостей ;
 –– алгебраические дополнения.
–– алгебраические дополнения.
Как и матрицу сопротивления, матрицу проводимостей можно составить по заданной схеме, зная правила формирования уравнений. Для этого заготавливается таблица с числом строк и столбцов, равным  . В клетки расположенные на главной диагонали, записываются собственные проводимости узлов, в остальные клетки - взаимные проводимости. Например, матрица проводимости схемы рисунок 2. 21 выглядит так
. В клетки расположенные на главной диагонали, записываются собственные проводимости узлов, в остальные клетки - взаимные проводимости. Например, матрица проводимости схемы рисунок 2. 21 выглядит так
1 23
|  |  |  | ||
 |  |  | |||
 |  |  |
Если одной из ветвей схемы является идеальный источник тока, то проводимость этой ветви полагается равной нулю, а ток источника тока учитывается дважды с разными знаками при записи вектор-столбца задающих узловых токов.
