Пример хаоса

Простейшим примером динамической модели, обнаруживающей хаотическое поведение, по-видимому, является логистическое уравнение, или уравнение роста популяции .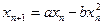

Первый член в правой части описывает рост или рождение, а нелинейный член ответствен за ограничение роста, связанное, например, с ограниченностью энергетических или пищевых ресурсов. Если пренебречь нелинейным членом 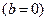, то можно выписать явное решение получающегося линейного уравнения: ,

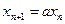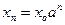
Это решение устойчиво при 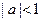и неустойчиво при 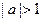. В последнем случае из линейной теории следует нереалистичное предсказание неограниченного роста.

Нелинейную модель обычно переписывают в безразмерном виде .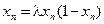

При 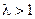имеются две точки равновесия (т. е. ).

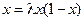Для выяснения устойчивости отображения 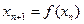следует вычислить величину наклона 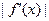в точке покоя. Если 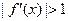, точка покоя неустойчива.

При 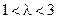логистическое уравнение имеет две точки покоя: 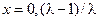. При этом начало координат – неустойчивая точка, а вторая точка покоя устойчива.

Однако при 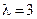наклон при 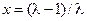превышает единицу 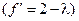и обе точки равновесия становятся неустойчивыми.

При значениях параметра 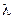, заключенных между 3 и 4, это простое разностное уравнение описывает множество многопериодических и хаотических движений. При 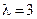становится неустойчивым стационарное решение, но остается устойчивым бицикл или двупериодическая орбита. Эта орбита показана на рисунке. Величина 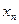повторяется через каждую итерацию.

При дальнейшем увеличении 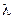двупериодическая орбита становится неустойчивой и возникает цикл с периодом 4, который вследствие бифуркации быстро заменяется циклом с периодом 8 при еще больших значениях 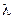. Этот процесс удвоения периода продолжается до тех пор, пока 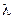не достигает значения 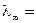3,56994 ....

Вблизи этого значения последовательность значений параметра, при которых происходят удвоения периода, подчиняется точному закону

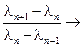4,66920.

Это предельное отношение называется числом Фейгенбаума – по имени физика, который обнаружил эти свойства рассматриваемого отображения(рисунок 1.70).

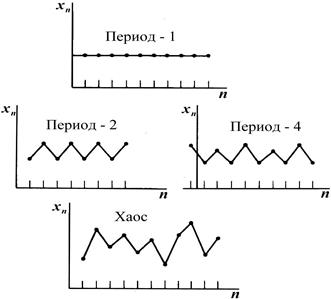
Рисунок 1.70 - Возможные типы решений логистического уравнения (квадратичного отображения)

При значениях 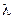, превышающих 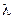, могут возникать хаотические итерации, т. е. поведение модели на больших временах не укладывается в рамки простого периодического движения. В интервале 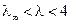также присутствуют определенные узкие интервалы 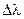, для которых существуют периодические орбиты.

Удвоение периода и отношение Фейгенбаума обнаруживаются во многих физических экспериментах. Это означает, что во многих непрерывных эволюционных процессах сведение к разностному уравнению с помощью сечения Пуанкаре приводит к квадратичному отображению; отсюда следует важная роль отображений в исследовании дифференциальных уравнений.

Заключительные замечания. Динамика – старейший раздел физики. И тем не менее через 300 лет после публикации Principia Ньютона (1687) появляются все новые открытия. Появившиеся за это время идеи Эйлера, Лагранжа, Гамильтона и Пуанкаре, родившись в небесной механике, проникли теперь во все области физики. Так же как новая наука, динамика, породила в XVII в. дифференциальное исчисление, в наше время нелинейная динамика ввела в обиход такие новые идеи геометрии и топологии как фракталы, без освоения которых ученому XX в. не удастся полностью понять предмет исследований.

Идеями хаоса западная мысль обязана еще древним грекам. Сами эти идеи сводились к объяснению порядка в том мире, который возник из первобытного мира – бесформенного, хаотичного и неупорядоченного. Но уже в восточной мысли, в частности, в даосизме хаос ассоциируется со структурами, вложенными в структуры, вихрями, вложенными в вихри, как это происходит, например, в течении жидкостей.

Вплоть до последнего десятилетия XX в. в динамике преобладало представление, что порядок возникает из окружающего бесформенного хаоса, и этот порядок узнается лишь по предсказуемой периодической структуре. Теперь эту точку зрения вытесняет другая концепция хаотических явлений. Они возникают согласно регулярным законам и за ними стоит не бесформенный хаос, но хаос с сокрытым порядком, фрактальными структурами. На пути этого изменения парадигм мы руководствуемся новыми математическими представлениями нашего «упорядоченного» мира.