Пример выполнения практической работы №4
1. Дана вычислительная система с горячим резервированием. Резервирование двукратное: 1 ЭВМ - рабочая, две – резервные (s=3). Среднее время наработки одной ЭВМ на отказ – 20 часов (интенсивность отказов λ = 1/t = 0.051/час). Интенсивность восстановления μ равно 0.1 1/час.
Определить вероятность того, что система является работоспособной (в начале работы все ЭВМ исправны). Решение получить в установившемся режиме (расчет с помощью аналитического решения и методом имитационного моделирования) и в переходном режиме, решая численным методом систему дифференциальных уравнений.
1.1 Решение задачи в среде MathCAD
Коэффициент готовности системы с горячим резервированием и с восстановлением вышедших из строя элементов вычисляем по формулам (22). Ниже приведен фрагмент
MATHCAD – программы:

Таким образом, вероятность безотказной работы системы (коэффициент готовности) в установившемся режиме равна 0,842.
Решение системы уравнений Колмогорова (15) методом Рунге – Кутты дается в следующем фрагменте:
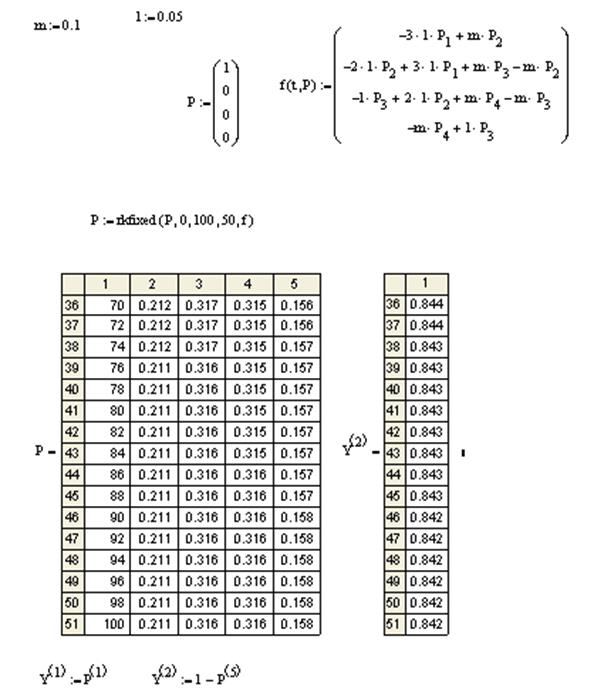
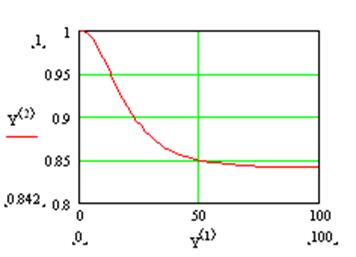
Рис. 9. Вероятность исправной работы системы с горячим резервированием
(и с восстановлением вышедших из строя элементов) как функция времени.
Результаты этих решений полностью совпадают .
Решение задачи методом имитационного моделирования.
Ниже приведены текст GPSS – программы и результаты ее работы.
RMULT 223
EXPON1 FUNCTION RN1,C24 EXPONENTIAL DISTRIBUTION
0,0/.100,.104/.200,.222/.300,.355/.400,.509/.500,.690/.600,.915/.700,1.200/.750,1.380/.800,1.600/
.840,1.830/.880,2.120/.900,2.300/.920,2.520/.940,2.810/.950,2.990/.960,3.200/.970,3.500/.980,3.900/
.990,4.600/.995,5.300/.998,6.200/.999,7/1,8
COMP STORAGE 3
GENERATE ,,,3
L1 ENTER COMP
ADVANCE 20,FN$EXPON1
LEAVE COMP
QUEUE LINE
SEIZE remont
DEPART LINE
ADVANCE 10,FN$EXPON1
RELEASE remont
TRANSFER ,L1
GENERATE 100
TEST E SE$COMP,0,L2
SEIZE NUMBER
RELEASE NUMBER
L2 TERMINATE 1
START 1000
START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 100000.000 15 2 1
NAME VALUE
COMP 10007.000
EXPON1 10006.000
L1 2.000
L2 15.000
LINE 10008.000
NUMBER 10010.000
REMONT 10009.000
LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY
1 GENERATE 3 0 0
L1 2 ENTER 7852 0 0
3 ADVANCE 7852 2 0
4 LEAVE 7850 0 0
5 QUEUE 7850 0 0
6 SEIZE 7850 0 0
7 DEPART 7850 0 0
8 ADVANCE 7850 1 0
9 RELEASE 7849 0 0
10 TRANSFER 7849 0 0
11 GENERATE 1000 0 0
12 TEST 1000 0 0
13 SEIZE 846 0 0
14 RELEASE 846 0 0
L2 15 TERMINATE 1000 0 0
FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY
REMONT 7850 0.788 10.043 1 4 0 0 0
NUMBER 846 0.000 0.000 1 0 0 0 0
QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
LINE 2 0 7850 3109 0.636 8.104 13.419 0
STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY
COMP 3 1 0 3 7852 1 1.575 0.525 0 0
FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE
4 0 100006.349 4 8 9
1 0 100040.889 1 3 4
1004 0 100100.000 1004 0 11
3 0 100109.907 3 3 4
Из 1000 проверок (транзакты, прошедшие через блок TEST) 846 закончились успешно. Вероятность исправной работы - 0.846. Расхождение результатов с аналитическим решением равно 0.4 процента! Очень высокая точность, которую можно еще повысить, увеличивая время моделирования.
1.2 Дана та же самая система, что и в пункте 1.1, только резервирование – холодное.
2.1 Решение задачи в среде MathCAD
Фрагмент MATHCAD – программы:
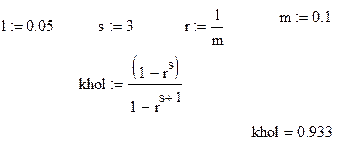
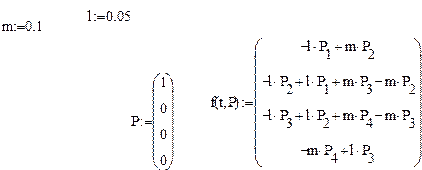
P:=rkfixed(P,0,100,50,f)
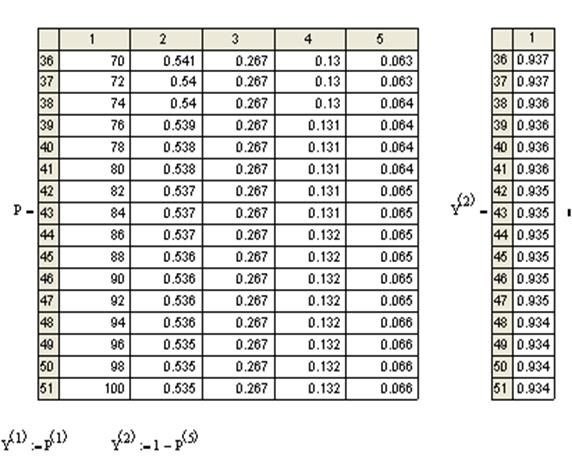
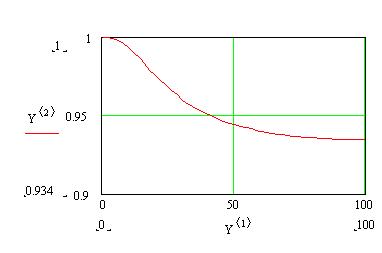
Рис. 10. Вероятность исправной работы системы с холодным резервированием
(и с восстановлением вышедших из строя элементов) как функция времени.
2.2 Решение задачи методом имитационного моделирования.
(текст GPSS – программы и результаты ее работы)
RMULT 223
EXPON1 FUNCTION RN1,C24 EXPONENTIAL DISTRIBUTION
0,0/.100,.104/.200,.222/.300,.355/.400,.509/.500,.690/.600,.915/.700,1.200/.750,1.380/.800,1.600/
.840,1.830/.880,2.120/.900,2.300/.920,2.520/.940,2.810/.950,2.990/.960,3.200/.970,3.500/.980,3.900/
.990,4.600/.995,5.300/.998,6.200/.999,7/1,8
GENERATE ,,,3
L1 SEIZE COMP
ADVANCE 20,FN$EXPON1
RELEASE COMP
QUEUE LINE
SEIZE remont
DEPART LINE
ADVANCE 10,FN$EXPON1
RELEASE remont
TRANSFER ,L1
GENERATE 100
TEST E F$COMP,1,L2
SEIZE NUMBER
RELEASE NUMBER
L2 TERMINATE 1
START 1000
START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 100000.000 15 3 0
NAME VALUE
COMP 10007.000
EXPON1 10006.000
L1 2.000
L2 15.000
LINE 10008.000
NUMBER 10010.000
REMONT 10009.000
LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY
1 GENERATE 3 0 0
L1 2 SEIZE 4590 0 0
3 ADVANCE 4590 1 0
4 RELEASE 4589 0 0
5 QUEUE 4589 1 0
6 SEIZE 4588 0 0
7 DEPART 4588 0 0
8 ADVANCE 4588 1 0
9 RELEASE 4587 0 0
10 TRANSFER 4587 0 0
11 GENERATE 1000 0 0
12 TEST 1000 0 0
13 SEIZE 931 0 0
14 RELEASE 931 0 0
L2 15 TERMINATE 1000 0 0
FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY
COMP 4590 0.938 20.427 1 4 0 0 0
REMONT 4588 0.461 10.041 1 1 0 0 0
NUMBER 931 0.000 0.000 1 0 0 0 0
QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
LINE 2 1 4589 2695 0.252 5.489 13.299 0
FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE
4 0 100010.314 4 3 4
1 0 100030.170 1 8 9
1004 0 100100.000 1004 0 11
Вероятность исправной работы системы (коэффициент готовности) равна 0.931!
