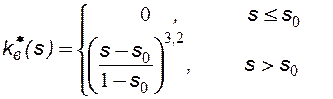
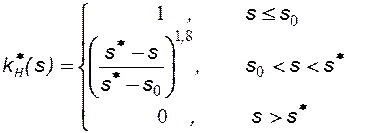Двухфазная фильтрация несмешивающихся жидкостей, вытеснение нефти водой. Функция Бакли – Леверетта.

Неустановившаяся фильтрация упругой жидкости

В упругой пористой среде

Неустановившиеся процессы возникают при пуске и остановке скважин, либо при изменении темпов отбора флюидов. Такие процессы характеризуются перераспределением давления, а также изменением скоростей фильтрационных потоков и дебитов во времени и зависят от упругих свойств пластов и насыщающих их жидкостей. Т.е. основной формой пластовой энергии, обеспечивающей приток жидкости к скважине, – энергия упругой деформации жидкости и материала пласта. При снижении пластового давления объём сжатой жидкости увеличивается, а объём порового пространства сокращается за счет расширения материала пласта, что определяет вытеснение жидкости из пласта в скважину. Хотя коэффициенты сжимаемости жидкости и пласта малы ( , ,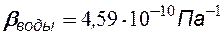

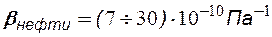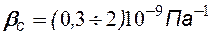), но зато велики объемы пластов и за счет этого при упругом режиме, могут быть значительные притоки жидкости.

Характерной особенностью упругого режима является то, что процесс перераспределения пластового давления очень медленный. Это связано с тем, что при фильтрации вязкой жидкости в пласте возникают большие силы сопротивления.

Подсчет упругого запаса жидкости в пласте.

Выделим V₀ – элемент объема пласта. Тогда, V_0ж – объем жидкости насыщающей этот элемент пласта при начальном давлении р₀ равен:

V_0ж = m V₀ (7.1)

В соответствии с законами Гука, изменение упругого запаса жидкости DV_з в объеме V₀ при изменении давления на Dр определяется как:

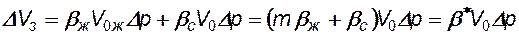(7.2)

где 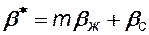- коэффициент упругоемкости пласта, численно равный изменению упругого запаса жидкости в единице объема при изменении пластового давления на единицу.

Продифференцировав (7.2) по времени 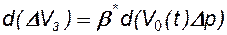и учитывая, что 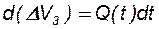, получим:

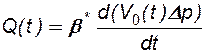(7.3)

Если формулы (7.1) - (7.3) относить к разрабатываемому в условиях замкнуто-упругого режима нефтяному месторождению, то под V₀ следует понимать объем пласта, в котором к данному моменту времени произошло изменение давления на величину Dр, при этом, 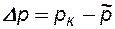, где 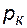- начальное пластовое давление; 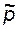- средневзвешенное по объему возмущенной части пласта V₀ давление. Вычислить средневзвешенное пластовое давление 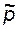можно, если известна геометрия возмущенной части пласта и конкретное распределение давления в ней, по формуле:

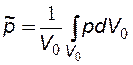. (7.4)

Уравнение пьезопроводности получено при совместном решении системы уравнений теории изотермической фильтрации и законов сжимаемости жидкости и пористой среды:

1) уравнение неразрывности,

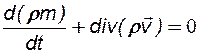(7.5)

2) закон Дарси,

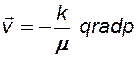; (7.6)

3) уравнение состояния сжимаемой жидкости:

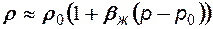; (7.7)

4) зависимость пористости от давления:

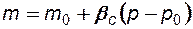. (7.8)

Подставив (7.6 – 7.8) в (7.5) и пренебрегая членами второго порядка малости, получим уравнение пьезопроводности:

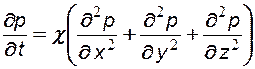- в дек. системе координат (7.9)

или

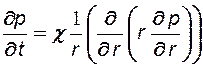- в случае осевой симметрии (7.10)

где: 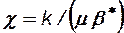- коэффициент пьезопроводности пласта, характеризующий темп перераспределения пластового давления в условиях упругого режима.

Некоторые точные решения уравнения пьезопроводности.

1. Плоско-параллельный случай, приток упругой жидкости в полубесконечном пласте к прямолинейной галерее скважин.

Для рассматриваемого одномерного движения жидкости уравнение пьезопроводности запишется в виде:

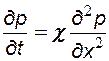(7.11)

Уравнение (7.11) решается при следующих начальных и граничных условиях:

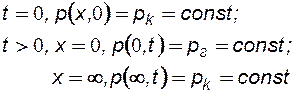(7.12)

Условия (7.12) можно интерпретировать таким образом: в начальный момент времени t = 0 пластовое давление было всюду в пласте одинаковым и равным р_к. При пуске скважины в момент времени t > 0 на галерее при х = 0 давление мгновенно упало до величины р_г, при этом на бесконечности x = ¥ давление остается постоянным и равным начальному пластовому р_к.

Решение задачи (7.11) - (7.12) получено методом автомодельной переменной и имеет следующий вид, рис.24:

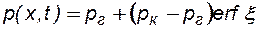(7.13)

где: 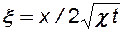- автомодельная переменная, а

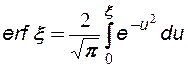- интеграл вероятности или интеграл Гаусса, который табулирован и имеется в математических справочниках.

Дебит галереи Q при x = 0 выражается в виде:

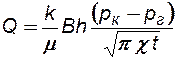, (7.14)

т.е. с течением времени Q убывает ~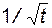

2. Плоско-радиальный случай реализуется в задаче о притоке упругой жидкости к скважине (точечному стоку или источнику) на плоскости в неограниченном пласте с постоянной мощностью и абсолютной проницаемостью.

В этом случае уравнение пьезопроводности имеет вид:

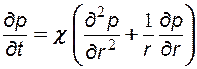, (7.15)

и решается при следующих граничных и начальных условиях:

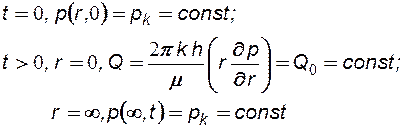(7.16)

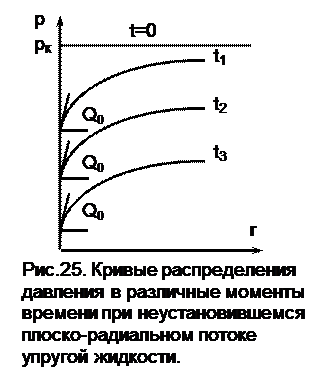Условия (7.16) интерпретируются иначе чем (7.12): в начальный момент времени t = 0 пластовое давление было всюду в пласте одинаковым и равным р_к. В момент времени t > 0 в точке r = 0 начинает работать добывающая скважина с постоянным объемным дебитом Q₀, на бесконечности r = ¥ давление остается неизменным и равным р_к.

Уравнение (7.15) при граничных условиях (7.16) также решается методом автомодельной переменной:

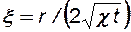. (7.17)

Перераспределение давления в пласте выражается, рис.25:

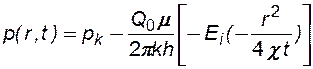, (7.18)

где: 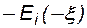- интегрально показательная функция, которая табулирована и имеется в математических справочниках.

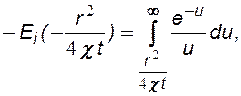(7.19)

Перераспределение дебита Q(r,t) в пласте:

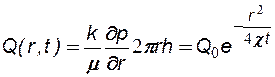(7.20)

Определение коллекторских свойств пласта по данным исследования скважин при упругом режиме. Кривые восстановления (падения) давления.

1. Метод касательной. После пуска или остановки скважины при помощи скважинных манометров снимают зависимость забойного давления от времени и строят график такой зависимости: при остановке скважины - кривую восстановления давления, при пуске скважины кривую падения давления. Обработка таких кривых основана на полученном решении (7.18), которое преобразуют, разложив интегрально-показательную функцию в ряд и ограничиваясь первыми двумя членами разложения:

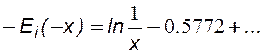(7.21)

При условии, что значение давления замеряют на забое и r = r_c, формула (7.18) записывается в виде:

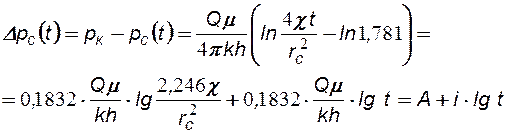(7.22)

где: 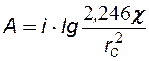, (7.23)

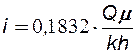(7.24)

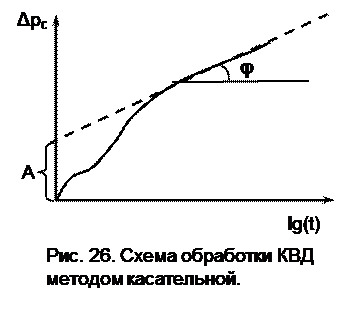Обычно кривую восстановле-ния (падения) давления строят в координатах Dр_с от lg(t). По прямому участку полученной кривой находится отрезок А, отсекаемый его продолжением на оси Dр_с и тангенс угла наклона j, равный i, рис.26. Затем по (7.23) и (7.24) определяют коэффициент гидропроводности пласта 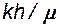и коэффициент пьезопроводности пласта c, по которым в свою очередь можно оценить фильтра-ционноемкостные характеристики горных пород.

Если скважина была пущена в эксплуатацию с постоянным дебитом Q и через промежуток времени T остановлена, но продолжает работать с тем же дебитом Q, то, используя метод суперпозиции, можно получить обобщенную формулу для обработки КВД методом касательной:

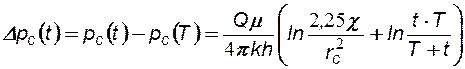(7.25)

В таком случае, удобнее кривую восстановления (падения) давления строить и анализировать в координатах Dр_с от ln(t×T/(t+T)).

2. Метод последовательной смены стационарных состояний (ПССС). Метод основан на предположении, что давление в пласте меняется во времени значительно медленнее, чем по координатам. Поэтому производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс.

В каждый момент времени вся область движения жидкости, в действительности охватывающая весь пласт, условно разделяется на две области - возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распределяется так, как будто бы движениё жидкости в ней установившееся: внешняя граница этой области служит в данный момент контуром питания. В невозмущенной области пласта давление всюду постоянно и равно начальному.

В соответствии с методом ПССС принимаем, что через время t после пуска скважины вокруг нее образуется возмущенная область радиусом R(t), где давление будет распределяться по стационарному закону:

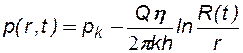(7.26)

Закон движения подвижной границы раздела возмущенной и невозмущенной областей определяется при помощи уравнения .материального баланса (7.3) и граничных условий:

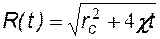(7.27)

Формула для анализа КВД принимает вид:

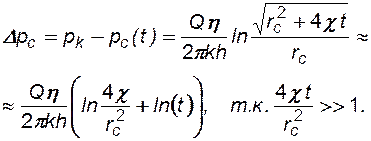(7.28)

А кривую восстановления (падения) давления удобней строить в координатах Dр_с от ln(t).

3. Метод Хорнера. В методе Хорнера реализован метод суперпозиции (наложения фильтрационных потоков) в теории упругого режима, что позволяет решать задачи, связанные с пуском, остановкой или с изменением темпа добычи скважины. Например, если скважина была пущена в эксплуатацию с постоянным дебитом Q и через промежуток времени T остановлена, но продолжает работать с тем же дебитом Q, то для обработки кривых восстановления давления скважин можно получить следующую формулу:

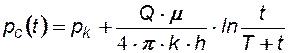, (7.29)

где T – время работы скважины с расходом Q.

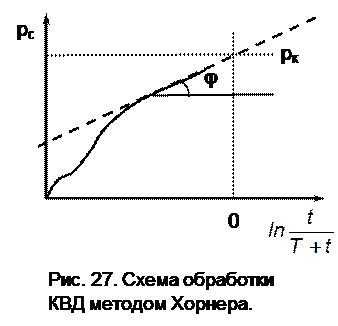Тогда кривую восстановления давления строят в координатах Dр_с от 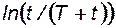, рис. 27. При этом, по углу наклона j определяется гидропроводность скважины:

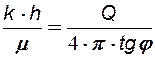, (7.30)

а, экстраполируя прямолинейный участок кривой восстановления давления до пересечения с прямой, параллельной оси ординат 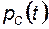и проведенной из точки 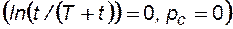, находят начальное пластовое давление .

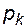Если дебит исследуемой скважины с момента пуска ее в эксплуатацию до момента остановки не оставался постоянным, то промежуток времени T можно подсчитать по приближённой формуле:

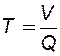, (7.31)

где V – накопленная добыча жидкости из скважины с момента пуска до момента остановки, Q – текущий установившийся дебит скважины непосредственно перед ее остановкой.

Задачи к разделу 7

Задача 7.1

Нефтяная залежь площадью S = 500 га и мощностью h = 30 м имеет пористость m = 20% и водонасыщенность s = 30%. Сколько нефти можно отобрать за счёт объёмного упругого расширения жидкости при падении давления от 29,4 МПа до 19,6 МПа, если коэффициент сжимаемости нефти β_н = 1,53∙10^-9 м²/Н, воды β_в = 3,06∙10^-10 м²/Н. Пласт считать недеформируемым.

Задача 7.2

Определить коэффициент нефтеотдачи при упругом режиме 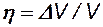- отношение объема добытой нефти за счёт упругого расширения нефти, воды и горной породы к первоначальному объему нефти в пласте, если площадь нефтеносности S_н =1000га, законтурная вода занимает площадь S_в = 10000га, мощность пласта h = 10 м, пористость пласта m = 25%, водонасыщенность в области нефтеносности s = 20%. Коэффициенты сжимаемости нефти, воды и породы соответственно равны β_н = 6,12∙10^-10 м²/Н, β_в = 4,28∙10^-10 м²/Н, β_с=2,04∙10^-10 м²/Н. Пластовое давление изменяется от 180 до 80 кгс/см².

Задача 7.3

Определить упругий запас нефти в замкнутой области нефтеносности площадью S = 4500 га, мощностью h = 15 м, пористостью m = 18% и насыщенностью связанной водой s = 20%, если средневзвешенное пластовое давление изменилось на 50 кгс/см². Коэффициенты сжимаемости нефти, воды и породы соответственно равны β_н = 2,04∙10^-9 м²/Н, воды β_в = 4,59∙10^-10 м²/Н, β_с = 1,02∙10^-10 м²/Н.

Задача 7.4

Определить время, за которое дебит галереи скважин, расположенной в полосообразном полубесконечном пласте, падает вдвое. Пласт шириной B = 700 м, мощностью h = 45 м, проницаемостью k = 0,8 Д, давление на галерее p_г = 9,8 МПа, на бесконечности (пластовое) p_к = 12,79 МПа. Коэффициенты сжимаемости жидкости и пласта равны соответственно β_ж = 1,53∙10^-9 м²/Н, β_с = 0,612∙10^-10 м²/Н, пористость m = 20%, вязкость жидкости μ = 1,5 мПа∙с.

Задача 7.5

В полосообразном полубесконечном пласте шириной B = 300 м, мощностью h = 15 м, пористостью m = 20%, сжимаемостью породы β_с=0,612∙10^-10 1/Па и проницаемостью k = 0,8 Д имеет место неустановившаяся фильтрация упругой жидкости с коэффициентом динамической вязкости μ = 1,5 мПа∙с и коэффициентом сжимаемости β_ж= 1,53∙10^-9 1/Па. Начальное пластовое давление и давление на галерее постоянны и, соответственно, равны p_к = 12,74 МПа и p_г=9,8МПа. Определить дебиты по точной формуле и по формуле, полученной по методу ПССС в момент времени t = 2 сут. Оценить погрешность при определении дебита по приближенной формуле.

Указание. При использовании метода ПССС сначала вывести закон движения границы возмущенной области .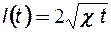

Задача 7.6

Определить изменение забойного давления на галерее в полосообразном полубесконечном пласте, если в момент t = 0 её начали эксплуатировать с постоянным дебитом Q = 500 м³/сут. Ширина галереи В = 400 м, мощность h = 18 м, коэффициент проницаемости k = 0,5 Д, коэффициенты сжимаемости жидкости β_ж = 2,04∙10^-9 м²/Н, породы β_с=0,51∙10^-10 м²/Н, коэффициент пористости m = 16%, коэффициент вязкости μ = 3 мПа∙с, начальное пластовое давление p_к = 14,7 МПа.

Задача 7.7

Определить коэффициенты гидропроводности и пьезопроводности пласта методом касательной по данным об изменении забойного давления совершенной скважины радиусом 10 см, дебит которой 100 м³/сут в условиях упругого режима. Начальное пластовое давление 150кгс/см². Изменение депрессии приведено ниже в таблице.

t	15 мин	1час	12час	1сут	5сут
Dр, кгс/см2	3,46	3,84	4,57	4,76	5,23

Задача 7.8

Определить коэффициенты гидропроводности и пьезопроводности пласта по данным в задаче 7.6, используя метод последовательной смены стационарных состояний.

Задача 7.9

Из совершенной скважины радиусом r_c = 0,1м, расположенной в бесконечном пласте, начали отбор нефти, поддерживая постоянное забойное давление p_с = 8,82 МПа. Начальное пластовое давление p_к = 11,76 МПа. Определить дебит скважины через 1час, 1 сутки и 1 месяц после начала эксплуатации, если коэффициент проницаемости k = 250мД, мощность пласта h = 12 м, коэффициент пьезопроводности пласта c =1,5×м²/с, вязкость жидкости μ = 1,3 мПа∙с, радиусом r_c = 0,1м.

Указание: При решении задачи использовать метод последовательной смены стационарных состояний, при этом вывести закон движения границы возмущенной области .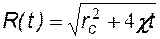

Задача 7.10

По следующим промысловым данным гидродинамических исследований двух независимых скважин определить максимальное количество неизвестных параметров.

Данные, используемые при интерпретации:
	Скважина № 1	Скважина № 2
Дебит перед остановкой, м3/сут
Время режима до остановки T, сут
Обводненность, доли единиц
Мощность пласта, м	3,4
Объемный коэффициент	1,12	1,1
Вязкость нефти, сПз	1,35	1,35
Сжимаемость нефти, 1/атм	8,2 10-5	1,99 10-4
Сжимаемость породы, 1/атм	3,76 10-6	4,1 10-5
Пористость, доли единиц	0,21	0,2
Радиус скважины истинный, м	0,108	0,108
	Скважина № 1		Скважина № 2
	t, час	Рзаб, атм	t, час	Рзаб, атм		t, час	Рзаб, атм	t, час	Рзаб, атм
		103,42		174,69			113,57	24,98	142,34
	0,5	106,54		178,14		1,65	123,82	26,65	142,46
		111,01		179,82		3,32	131,04	28,32	142,51
		124,51	26,5	183,51		4,98	134,67	29,98	142,65
	2,5	127,27	31,5	185,39		6,65	136,59	31,65	142,83
		130,99		187,93		8,32	137,82	33,32	142,96
	3,5	134,16		188,17		9,98	138,74	34,98	143,02
		140,00	55,5	188,64		11,65	139,38	36,65	143,15
	4,5	147,25	70,75	189,54		13,32	140,05	38,32	143,25
		148,38	79,5	190,21		14,98	140,51	39,98	143,37
		155,03	94,5	190,61		16,65	140,76	41,65	143,45
		164,26	99,08	190,78		18,32	141,2	43,32	143,52
		168,48				19,98	141,54	44,98	143,61
		171,75				21,65	141,84	46,65	143,7
		174,69				23,32	142,12	48,00	143,76

Указание: При решении задачи использовать методы Хорнера и касательной.

Двухфазная фильтрация несмешивающихся жидкостей, вытеснение нефти водой. Функция Бакли – Леверетта.

Углеводородные системы могут быть гомо- и гетерогенными. В гомогенной системе все ее части имеют одинаковые физические и химические свойства. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза - это часть системы, которая является гомогенной и отделена от других фаз отчетливыми границами.

Насыщенностью i -й фазы s_i называется доля объема порового пространства, занятого этой фазой:

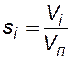, (8.1)

Сумма всех насыщенностей в поровом объеме равна единице.

Если поровое пространство пористой среды заполнено только двумя жидкостями - нефтью и водой, то тогда выполняется соотношение:

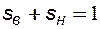, (8.2)

где s_н , s_в - соответственно насыщенности нефтью и водой.

Далее введем обозначения:

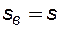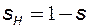, , (8.3)

В общем случае при описании двухфазной фильтрации увеличивается число параметров, подлежащих определению, что существенно усложняет теоретическое исследование. Далее, рассмотрим наиболее простое, с точки зрения математического моделирования, одномерное двухфазное течение, соответствующее вытеснению жидкости, первоначально заполнявшей поры, другой жидкостью, не смешивающейся с первой, впервые предложенное американскими исследователями С. Бакли и М. Левереттом (1942 г.).

Нефть вытесняется водой в прямолинейном тонком горизонтальном образце, который представлен однородной изотропной пористой средой при следующих допущениях:

1) вода, нефть и пористая среда несжимаемы, т. е.:

;

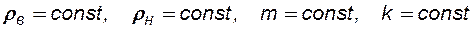2) капиллярные силы пренебрежимо малы, т.е. пластовое давление в нефти и воде одинаковое:

;

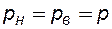3) влияние массовых сил не учитывается;

4) температура постоянна;

5) фазовые переходы и химические реакции отсутствуют.

С учетом сделанных допущений и (8.3), уравнения неразрывности для воды и нефти примут вид:

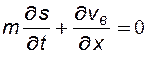, (8.4)

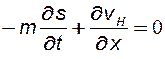(8.5)

Сложив уравнения (8.4) и (8.5) получим:

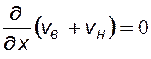(8.6)

Уравнение (8.6) показывает, что суммарная скорость двухфазного потока v(t) (или суммарный расход обеих жидкостей Q(t)) не зависит от координаты x и является либо постоянной величиной, либо известной функцией времени:

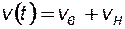или 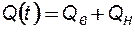. (8.7)

Скорости фильтрации воды 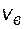и нефти 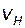подчиняются закону Дарси, который записывается для каждой из жидкостей отдельно:

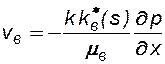, (8.8)

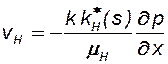. (8.9)

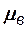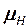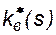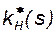где , - коэффициенты динамической вязкости соответственно воды и нефти, k – абсолютная проницаемость (определяемая по какой либо одной из жидкостей или газу), а и - относительные фазовые проницаемости воды и нефти, характеризующие долю проводимости среды для соответствующей фазы при данной насыщенности.

Отметим, что произведение k на 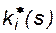характеризует фазовую проницаемость i -ой жидкости 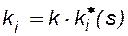, как проницаемость в обычном смысле (абсолютную) только в условиях совместной фильтрации.

Относительные фазовые проницаемости 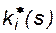определяются экспериментально, являются в основном функциями насыщенности соответствующей фазой и изменяются в пределах от 0 до 1, возрастая с ростом насыщенности.

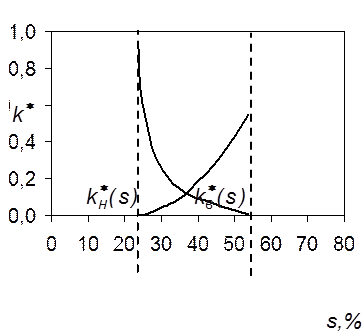
Типичные экспериментальные кривые фазовых проницаемостей, определяемые при совместной фильтрации воды и нефти, приведены на рисунке 28.

	Рис. 28. Кривые зависимости относительных фазовых проницаемостей от водонасыщенности при вытеснении нефти водой.

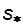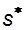Отметим некоторые характерные особенности этих кривых. Для каждой жидкости существует предельная насыщенность, такая, что при меньших значениях насыщенности эта жидкость неподвижна.

Движение воды может происходить только в том случае, если 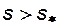, где 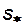- называют насыщенностью связанной водой (или коэффициентом водоудерживающей способности). Следует понимать, что величина остаточной водонасыщенности 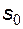(начальное содержание воды в пласте) зачастую отличается от величины насыщенности связанной водой. Это связано с особенностями формирования реальных нефтенасыщенных пластов. Величина 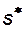- конечная насыщенность водой, при которой нефть неподвижна, т.е. фильтруется только вода. Величина 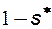называется остаточной нефтенасыщенностью, или количество остаточной нефти, которое не может быть вытеснено из пористой среды водой, сколь бы длительным не было вытеснение. Таким образом, совместное течение двух фаз имеет место лишь в следующем интервале изменения насыщенности водой:

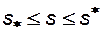. (8.10)

Относительная проницаемость смачивающей фазы (воды) 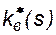при 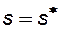имеет значение, меньше 1, тогда как величина 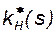при 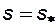близка к единице. Это означает, что присутствие связанной смачивающей фазы мало влияет на течение несмачивающей жидкости (нефти), тогда как присутствие остаточной нефти значительно «стесняет» движение воды.

Разделив уравнение (8.8) на сумму уравнений (8.8) и (8.9), с учетом (8.7), можно получить:

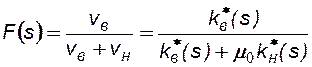, (8.11)

где 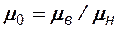, а F(s) – функция насыщенности, называемая функцией распределения потоков Бакли - Леверетта.

Функция F(s) имеет простой физический смысл – объемная доля воды в суммарном потоке двух несмешивающихся жидкостей. Функция Бакли – Леверетта играет важную роль при гидродинамических расчетах двухфазных потоков, определяя полноту вытеснения и характер распределения насыщенности по пласту. Характерный вид функции Бакли-Леверетта представлен на рис. 29.

Из (8.11) следует:

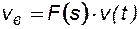. (8.12)

Подставив (8.12) в (8.8) и используя правило дифференцирования сложной функции, получим уравнение только относительно s:

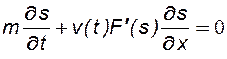. (8.13)

где 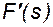- производная функции Бакли-Леверетта по s, рис.29.

Уравнение (8.13) решается методом характеристик:

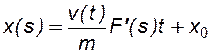, (8.14)

где x₀ координата с начальной водонасыщенностью s₀ при t = 0.

Формулу (8.14) можно проинтерпретировать следующим образом: точка с постоянной насыщенностью движется с постоянной скоростью, пропорциональной v/m, и является функцией самой насыщенности.

Для нахождения профиля водонасыщенности в любой момент времени необходимо ввести начальное и граничное условия. Например, если на входе в образец, изначально (t = 0) насыщенный нефтью с равномерно распределенной остаточной водонасыщенностью s₀, закачивают только воду (F(s) = 1 в точке x = 0), то начальное и граничное условия примут вид:

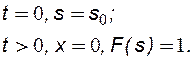(8.15)

Как видно из рисунка 29, одному и тому же значению 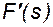, определяющему скорость распространения насыщенности заданной величины, соответствуют два разных значения насыщенности s. Это означает, что, начиная с некоторого момента времени, распределение насыщенности становится многозначным, что физически невозможно.

Такая многозначность решения снимается, если ввести скачок насыщенности, положение которого определяется из условия материального баланса на скачке.

Рис. 29. Характерный вид функции Бакли-Леверетта F(s) и ее производной F’(s). Определение основных параметров вытеснения по функции Бакли-Леверетта за безводный период.

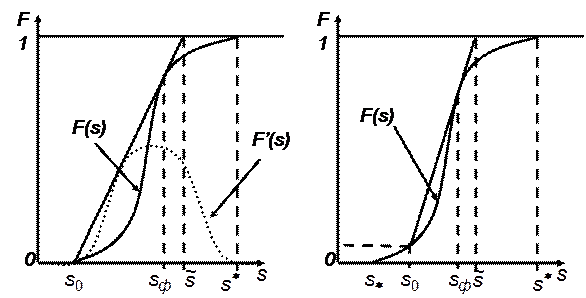
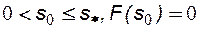
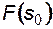а) б)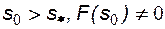

Тогда можно определить значение насыщенности на фронте вытеснения (на скачке) из соотношения:

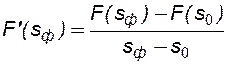. (8.16)

Уравнение имеет простую геометрическую интерпретацию – уравнение касательной, проведенной из точки (s₀, F(s₀)) к кривой F(s), где s_ф – абсцисса точки касания, рис.29.

Скорость фронта вытеснения, с учетом (8.14) при x₀=0, определяется из соотношения

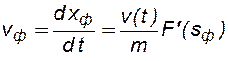. (8.17)

Определить среднюю водонасыщенность за фронтом вытеснения (в зоне совместного течения воды и нефти) в безводный период добычи (на выход из образца или на выходное сечение пласта поступает одна только нефть), определяемую как отношение объема воды, содержащейся в пласте к моменту времени t, к объему порового пространства в зоне смеси, можно из соотношения:

. (8.18)

Графически 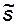можно определить по точке пересечения касательной к кривой F(s), определяющей фронтальную насыщенность, с прямой F(s)=1.

Определить время прорыва воды (момент появления воды на выходе из образца или на выходном сечении пласта) можно из решения уравнения (8.14) при x₀=0, положив х=L (L – длина образца или пласта) и s = s_ф:

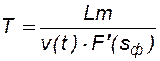. (8.19)

Одним из важнейших параметров разработки нефтяных месторождений является коэффициент нефтеотдачи пласта.

Коэффициент нефтеотдачи - отношение количества извлеченной из пласта нефти к первоначальным ее запасам в пласте. Различают текущую и конечную нефтеотдачу. Под текущей нефтеотдачей понимают отношение количества извлеченной из пласта нефти на данный момент разработки пласта к первоначальным ее запасам. Ее величина переменна во времени и возрастает по мере увеличения количества извлеченной из пласта нефти. Конечная нефтеотдача - отношение количества добытой нефти к первоначальным ее запасам в конце разработки пласта.

Нефтеотдача вообще зависит от многих факторов. Обычно выделяют факторы, связанные с самим механизмом извлечения нефти из пластов, и факторы, характеризующие полноту вовлечения пласта в целом в разработку.

Коэффициент текущей нефтеотдачи пластов 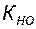при их разработке с применением заводнения представляют в виде следующего произведения:

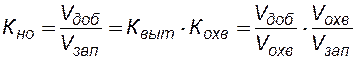(8.20)

где: 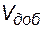- объем добытой из пласта нефти за определенный период времени, 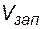- общий объем геологических запасов нефти, 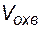- объем запасов нефти, охваченных заводнением.

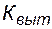- коэффициент вытеснения нефти из пласта – величина, равная отношению количества вытесненной из пласта нефти к запасам нефти, первоначально находившимся в части пласта, вовлеченной в разработку. Отметим, что для текущей нефтеотдачи коэффициент вытеснения величина переменная во времени.

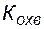- коэффициент охвата пласта разработкой – величина, равная отношению запасов нефти, вовлеченных в разработку, к общим геологическим запасам нефти в пласте.

В некоторых случаях коэффициент нефтеотдачи равен произведению не только двух, но и трех и большего числа коэффициентов:

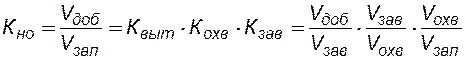(8.21)

где: 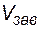- первоначальный объем нефти в заводненной области пласта, а 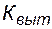- коэффициент вытеснения нефти водой из заводненной области пласта через определенный момент времени, 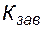- коэффициент заводнения – отношение объема нефти, в охваченной заводнением области пласта к первоначальным запасам в этой области.

Для плоскопараллельного случая, когда пласт однороден с постоянным распределением насыщенности по всей его длине и разрабатывается одной добывающей и одной нагнетательной цепочками скважин (а также при анализе результатов лабораторных экспериментов) при определении коэффициента нефтеотдачи можно не учитывать коэффициенты охвата и заводнения, приняв их равными 1.

Тогда коэффициент вытеснения за безводный период определяют по формуле:

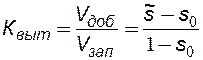. (8.22)

Задачи к разделу 8

Задача 8.1

Построить функцию Бакли-Леверетта при вытеснении нефти водой с соотношением вязкостей 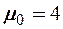по следующим экспериментальным данным об относительных фазовых проницаемостях:

s, %
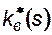				0,01	0,05	0,11	0,21	0,33	0,51	0,72	-
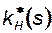	-	-	0,7	0,5	0,34	0,23	0,13	0,06	0,02

Определить значение насыщенности на фронте 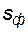и среднюю насыщенность порового пространства водой в зоне вытеснения .

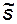Задача 8.2

Определить положение фронта вытеснения нефти водой в плоско- параллельном случае в различные моменты времени (1ч, 12 ч, 1 сут, 2сут, 5 сут, 10 сут), если пористость пласта m = 20%, ширина фильтрационного потока B = 500м, мощность пласта h = 10м, дебит галереи Q = 21600 м³/сут, а по экспериментальным данным снята зависимость функции Бакли-Леверетта F от водонасыщенности s:

s, %	23,8	27,8	29,1		34,5	61,05
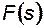		0,2	0,4	0,6	0,8

Задача 8.3

Даны зависимости относительных фазовых проницаемостей воды 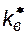и нефти 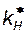от водонасыщенности s. Построить распределение водонасыщенности в полосообразном пласте при t = 0,5сут. Определить коэффициент вытеснения нефти, среднюю водонасыщенность в момент прорыва воды к нагнетательным скважинам и время прорыва.

Вязкость нефти μ_н = 7 мПа∙с, вязкость воды μ_в = 1 мПа∙с, остаточная водонасыщенность s₀ = 0,2, остаточная нефтенасыщенность s_н^ост = 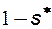= 0,35.

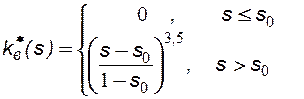
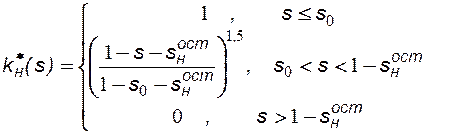
Задача 8.4

Даны зависимости относительных фазовых проницаемостей воды 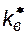и нефти 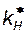от водонасыщенности s. Сопоставьте коэффициенты вытеснения нефти на момент прорыва чистой воды и загущенной полимером воды. Вязкость нефти μ_н = 20 мПа∙с, вязкость воды μ_в = 1 мПа∙с, вязкость воды с полимером μ_вп = 15 мПа∙с, остаточная водонасыщенность s₀ = 0,2, конечная водонасыщенность 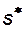= 0,75.

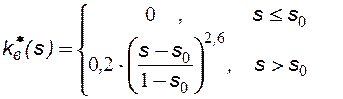
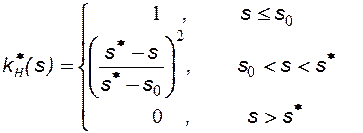
Задача 8.5

Даны зависимости относительных фазовых проницаемостей воды 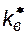и нефти 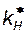от водонасыщенности s. Сравнить коэффициенты вытеснения нефти за безводный период водой и водой с растворенным в ней ПАВом (поверхностно-активным веществом).

Вязкость нефти μ_н = 7 мПа∙с, вязкость воды μ_в = 1 мПа∙с, остаточная водонасыщенность s₀ = 0,3, конечная водонасыщенность при вытеснении нефти водой 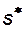= 0,65, а конечная водонасыщенность при вытеснении нефти водой с ПАВом 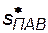=0,75.