Изучение законов вращения на крестообразном
МАЯТНИКЕ ОБЕРБЕКА
Цель работы: изучение законов вращательного движения твердого тела.
Приборы и принадлежности: маятник Обербека, штангенциркуль, набор грузов.
Теоретические сведения
В механике под твердым телом подразумевают абсолютно твердое тело, т.е. тело, деформациями которого можно пренебречь. При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Быстроту вращения характеризуют углом поворота тела в единицу времени. Если за любые равные промежутки времени тело поворачивается на одинаковые углы, вращение называется равномерным, а величина ω=φ/t определяет угол поворота в единицу времени и называется угловой скоростью. Единицей измерения угловой скорости служит радиан в секунду (рад/с).
При неравномерном вращении изменение угловой скорости со временем характеризуется векторной величиной, которая называется угловым ускорением 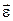 . Модули угловой скорости и углового ускорения связаны с линейной скоростью v и тангенциальной составляющей ускорения аτ следующими соотношениями:
. Модули угловой скорости и углового ускорения связаны с линейной скоростью v и тангенциальной составляющей ускорения аτ следующими соотношениями:
 , аτ
, аτ  , (4.1)
, (4.1)
где r - расстояние точки до оси вращения.
При вращении тела вокруг неподвижной оси изменение угловой скорости и его движения зависит от действующего момента силы. Моментом силы 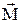 относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора
относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора 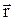 , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу 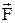 (рис. 4.1):
(рис. 4.1):
 Рис. 4.1 Рис. 4.1 |  , (4.2) где , (4.2) где 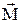 - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 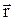 к к 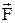 . Модуль момента силы: . Модуль момента силы:  , (4.3) где α - угол между , (4.3) где α - угол между 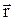 и и 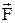 ; ;  - плечо силы - кратчайшее расстояние между линией действия силы и точкой О. - плечо силы - кратчайшее расстояние между линией действия силы и точкой О. |
Моментом силы относительно неподвижной оси z,называется скалярная величина Мz, равная проекции на эту ось вектора 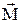 момента силы, определенного относительно произвольной точки О, лежащей на оси z (рис. 4.2). Значение момента Мz не зависит от выбора положения точки О на оси z.
момента силы, определенного относительно произвольной точки О, лежащей на оси z (рис. 4.2). Значение момента Мz не зависит от выбора положения точки О на оси z.
 Рис. 4.2 Рис. 4.2 | Если ось z совпадает с направлением 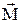 , то момент силы представляется в виде вектора, совпадающего с осью: , то момент силы представляется в виде вектора, совпадающего с осью:  . (4.4) Равнопеременное вращательное движение тел характеризуется постоянным угловым ускорением, оно появляется под действием сил, момент которых постоянен по величине и направлению. . (4.4) Равнопеременное вращательное движение тел характеризуется постоянным угловым ускорением, оно появляется под действием сил, момент которых постоянен по величине и направлению. |
Зависимость углового ускорения от момента силы выражена в основном законе динамики вращательного движения:
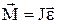 , (4.5)
, (4.5)
где J - момент инерции тела; ε - угловое ускорение.
Момент инерции J материальной точки относительно какой-либо оси вращения называется произведением массы m этой точки на квадрат расстояния r от точки до оси вращения:
J=mr2. (4.6)
Моментом инерции тела относительно данной оси вращения называют сумму моментов инерции элементарных масс, на которые разбивается тело:
 , (4.7)
, (4.7)
где 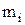 - элементарная масса;
- элементарная масса;  - расстояние элементарной массы до оси вращения.
- расстояние элементарной массы до оси вращения.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту инерции Jc относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния а между осями:
J=Jc+ma2. (4.8)
Описание установки
Общий вид маятника Обербека показан на рис. 4.3. На вертикальной колонне (1), установленной на основании (2), прикреплены два кронштейна: нижний неподвижный (3) и верхний подвижный (4) и две неподвижные втулки: нижняя (5) и верхняя (6). Основание снабжено регулируемыми ножками (7), обеспечивающими горизонтальную установку прибора.

Рис. 4.3
На верхней втулке (6) посредством основания (8) закреплен подшипниковый узел диска(9) и диск (10). Через диск перекидывается нить (11). Один конец нити прикреплен к двухступенчатому диску (12), а на втором конце закреплены грузы (13). На нижней втулке (5) посредством основания (14) прикреплен тормозной электромагнит (15), который удерживает систему крестовины вместе с грузами в состоянии покоя. Подвижный кронштейн (4) можно переместить вдоль колонны и фиксировать его в любом положении, определяя таким образом длину пути падающего груза. Для этого на колонне (1) нанесена миллиметровая шкала (16). На неподвижном кронштейне (3) закреплен фотоэлектрический датчик (18). К кронштейну (3) прикреплен кронштейн (19) с резиновым амортизатором, ограничивающим движение грузов. На основании прибора имеется миллисекундомер.
Под действие падающего груза (13) нить разматывается с диска и вызывает равноускоренное вращательное движение крестовины. Угловое ускорение при этом тем меньше, чем больше момент инерции системы относительно оси вращения, величина которого зависит от положения перемещаемых грузов на крестовине.
Диск вращается равноускоренно под действием натянутой нити, силу натяжения которой можно найти по второму закону Ньютона:
 , (4.9)
, (4.9)
где P=mg - сила тяжести; Т - сила натяжения нити; m - масса падающего груза. Отсюда
 , (4.10)
, (4.10)
где g - ускорение свободного падения.
Вращательный момент силы, приложенной к крестовине,
 , (4.11)
, (4.11)
где r - радиус диска.
Так как поступательное движение падающего груза равноускоренное без начальной скорости, то  . Ускорение груза:
. Ускорение груза:
 , (4.12)
, (4.12)
где h - высота падения груза; t - время падения груза.
Поскольку линейное ускорение груза а равно тангенциальной составляющей ускорения аτ точки окружности диска, то угловое ускорение:
 . (4.13)
. (4.13)
Используя формулы (4.5), (4.11) и (4.13), получаем выражение для момента инерции, определяемого экспериментально,
 . (4.14)
. (4.14)
Теоретическое значение момента инерции маятника можно найти следующим образом:
 , (4.15)
, (4.15)
где  - суммарный момент инерции двухступенчатого диска, оси и втулки крестовины;
- суммарный момент инерции двухступенчатого диска, оси и втулки крестовины;  - момент инерции подвижных грузов крестовины;
- момент инерции подвижных грузов крестовины; 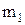 - масса подвижного груза на крестовине; R - расстояние от оси вращения до груза;
- масса подвижного груза на крестовине; R - расстояние от оси вращения до груза;  - момент инерции крестовины без груза;
- момент инерции крестовины без груза;  - масса стержня без груза;
- масса стержня без груза; 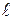 - длина стержня крестовины. В связи с тем, что размеры грузов малы по сравнению с расстоянием R от оси вращения до центров масс грузов, их моменты инерции можно определить как моменты инерции материальных точек. Оставив постоянной массу падающего груза m, будем изменять расстояние от оси вращения до подвижных грузов
- длина стержня крестовины. В связи с тем, что размеры грузов малы по сравнению с расстоянием R от оси вращения до центров масс грузов, их моменты инерции можно определить как моменты инерции материальных точек. Оставив постоянной массу падающего груза m, будем изменять расстояние от оси вращения до подвижных грузов 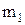 на крестовине.
на крестовине.
Соответственно для двух различных расстояний  и
и  моменты инерции будут определяться так:
моменты инерции будут определяться так:

 .
.
Найдем разность моментов инерции, исключив при этом слагаемые  и
и  .
.
 . (4.16)
. (4.16)
Порядок выполнения работы
1. Установить избранное число грузов и определить массу падающего груза m по формуле  , где
, где  - масса постоянного груза (она указана на установке);
- масса постоянного груза (она указана на установке); 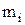 - масса каждого дополнительного груза (она указана на самом грузе). Масса подвижного груза
- масса каждого дополнительного груза (она указана на самом грузе). Масса подвижного груза 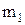 , укрепленного на стержне крестовины, указана на установке. Радиус r диска, на который намотана нить, измерить штангенциркулем.
, укрепленного на стержне крестовины, указана на установке. Радиус r диска, на который намотана нить, измерить штангенциркулем.
2. Укрепить на стержнях крестовины грузы m1 на одинаковых расстояниях  от оси вращения и измерить эти расстояния.
от оси вращения и измерить эти расстояния.
3. Груз массой m поднять на высоту h и установить его так, чтобы нижний край груза совпал с верхней гранью фотоэлектрического датчика 17.
4. Отсчитать по шкале, расположенной на колонне, высоту h падения груза.
5. Включить сетевой шнур в сеть питания.
6. Нажать кнопку «сеть» и проверить, показывают ли «0» все индикаторы на цифровом табло и горят ли лампочки обоих фотоэлектродов.
7. Опустив груз, одновременно нажать кнопку «пуск».
8. Записать значение времени падения груза с высоты h по миллисекундомеру.
9. Нажать кнопку «сброс».
10. Переместить падающий груз в верхнее первоначальное положение и
отжать кнопку «пуск».
11. Удостовериться, что произошло обнуление и блокировка схемы (т.е. груз самостоятельно не приходит в движение).
12. Повторить измерения времени 5 раз и определить среднее значение времени падения груза по формуле:
 ,
,
где n – число опытов.
13. Изменить положение грузов на стержнях крестовины и измерить расстояние R2 от оси вращения.
14. Провести измерения согласно пунктам 8-13. Результаты измерений
записать в таблицу.
Таблица
| № | m, кг |  ,кг ,кг | r, м | h, м |  ,м ,м |  | R2,м |  |
| t1 ср | t2 ср |
15. По формуле (4.14) вычислить моменты инерции JЭ1 и JЭ2, подставив
среднее значение времени, и найти их разность  .
.
16. По формуле (4.16) вычислить теоретическое изменение момента инерции  .
.
17. Сравнить полученные результаты и найти относительную погрешность измерения момента инерции по формуле:
 ,
,
где  - теоретическое изменение момента инерции;
- теоретическое изменение момента инерции;  - экспериментальное изменение момента инерции.
- экспериментальное изменение момента инерции.
18. Выполнение пунктов 16- 17 можно проводить на ЭВМ.
Контрольные вопросы
1. Дать определение абсолютно твердого тела.
2. Дать определение угловой скорости, углового ускорения. Какова связь
между линейными и угловыми скоростями и ускорениями? Единицы измерения угловой скорости, углового ускорения.
3. Почему движение падающего груза и вращение маховика являются
равноускоренными?
4. Что называется моментом силы относительно неподвижной оси? Как
определяется его направление? В каких единицах он измеряется?
5. Вывести основной закон динамики вращательного движения.
6. Какая сила сообщает вращающий момент маятнику? Как направлен
момент этой силы?
ЛАБОРАТОРНАЯ РАБОТА №5
