Замкнутые системы массового обслуживания
Простейшие потоки событий
Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Такой поток можно изобразить как последовательность точек t1...tn на числовой оси, соответствующих случайным моментам появления событий (рис.1.):

Рис.1. Последовательность однородных событий
Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени зависит только от длины этого участка и не зависит от того, где именно на оси 0t расположен этот участок.
Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Поток событий называется ординарным, если вероятности попадания на участок времени малой длины двух или более событий пренебрежимо малы по сравнению с вероятностью попадания на этот участок одного события.
Стационарность потока означает, что вероятностные характеристики этого потока не должны меняться в зависимости от времени. Например, такая характеристика, как интенсивность потока событий, равная математическому ожиданию числа событий в единицу времени, должна оставаться постоянной для стационарного потока.
На практике часто встречаются потоки событий, которые стационарны только на ограниченном участке времени. Например, поток вызовов, поступающих на телефонную станцию в дневное время, может считаться таковым. Тот же поток в течение целых суток уже не будет стационарным, поскольку ночью интенсивность вызовов гораздо меньше, чем днем.
Отсутствие последействия в потоке означает, что события появляются в последовательные моменты времени независимо друг от друга. Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последействия потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не другой момент, не связаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последействия может быть нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последействия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой.
Ординарность потока означает, что события в потоке приходят поодиночке, а не парами, тройками и т. д. Например, поток клиентов, направляющихся в парикмахерскую, практически можно считать ординарным, чего нельзя сказать о потоке клиентов, идущих в ЗАГС для регистрации брака.
Простейший поток играет среди потоков событий особую роль, до некоторой степени аналогичную роли нормального закона среди других законов распределения. Согласно центральной предельной теореме, при суммировании большого числа независимых случайных величин, подчиненных практически любым законам распределения, получается случайная величина, приближенно распределенная по нормальному закону. Аналогично можно сказать, что при суммировании (взаимном наложении) большого числа ординарных, стационарных потоков с практически любым последействием получается поток, сколь угодно близкий к простейшему. Условия, которые должны для этого соблюдаться, аналогичны условиям центральной предельной теоремы, а именно: складываемые потоки должны оказывать на сумму приблизительно равномерно малое влияние.
Замкнутые системы массового обслуживания
Рассмотрим системы массового обслуживания, в которых интенсивность потока поступающих заявок зависит от состояния самих систем. Такие системы массового обслуживания называются замкнутыми.
Пусть система состоит из п каналов обслуживания и т источников заявок, т>п.
Предположим, что каждый источник порождает простейший поток заявок с интенсивностью 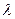 , причем источник не может посылать следующую заявку до завершения обслуживания своей предыдущей заявки (в этом и выражается замкнутость данной системы). Предположим также, что каждый канал порождает простейший поток обслуженных заявок с интенсивностью
, причем источник не может посылать следующую заявку до завершения обслуживания своей предыдущей заявки (в этом и выражается замкнутость данной системы). Предположим также, что каждый канал порождает простейший поток обслуженных заявок с интенсивностью 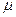 . Все состояния данной системы можно разбить условно на три группы:
. Все состояния данной системы можно разбить условно на три группы:
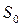 - "все каналы свободны",
- "все каналы свободны",
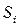 - "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n,
- "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n,
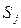 - "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ..., m.
- "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ..., m.
Графически все возможные переходы из состояния в состояние, а также интенсивности потоков событий, под воздействием которых эти переходы возможны, можно изобразить в виде размеченного графа так, как это показано на рис.2. Действительно, если система находится в состоянии 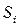 i = 0, 1,..., n - 1, то в состояние "i+ 1 каналов занято" она может перейти под воздействием суммарного потока заявок от m - i источников с интенсивностью
i = 0, 1,..., n - 1, то в состояние "i+ 1 каналов занято" она может перейти под воздействием суммарного потока заявок от m - i источников с интенсивностью 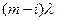 ; из состояния
; из состояния 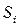 в состояние
в состояние 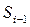 "i- 1 каналов занято" она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов обслуживания с интенсивностью
"i- 1 каналов занято" она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов обслуживания с интенсивностью 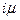 .. Напомним, что i источников прекращают поставку заявок до завершения обслуживания своих последних заявок. Если же система находится в состоянии
.. Напомним, что i источников прекращают поставку заявок до завершения обслуживания своих последних заявок. Если же система находится в состоянии 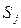 , j = n,...,m- 1, то в состояние
, j = n,...,m- 1, то в состояние 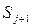 она может перейти под воздействием суммарного потока заявок с интенсивностью
она может перейти под воздействием суммарного потока заявок с интенсивностью 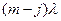 , а в состояние
, а в состояние 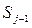 — под воздействием суммарного потока обслуженных заявок с интенсивностью
— под воздействием суммарного потока обслуженных заявок с интенсивностью 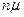 , поступающего от n каналов обслуживания.
, поступающего от n каналов обслуживания.

Рис. 2. Размеченный граф многоканальной замкнутой СМО
Составим на основе этого размеченного графа уравнения Колмогорова. Эти уравнения представляют собой систему линейных дифференциальных уравнений, описывающую вероятности Pr(t) нахождения данной системы в состоянии Sr в момент времени t, r = 0, 1, ..., m :
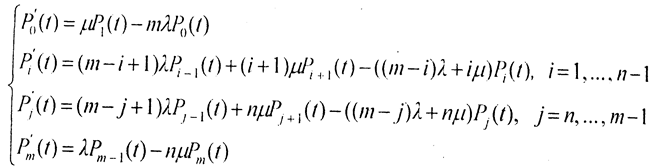
Особый интерес представляют вероятности Pr(t) в предельном стационарном режиме, т. е. при 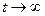 , которые называются предельными вероятностями состояний системы.
, которые называются предельными вероятностями состояний системы.
