ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. Предположим, что задано поперечное сечение произвольной формы, контур которого с достаточной степенью точности может быть представлен отрезками ломаных

Предположим, что задано поперечное сечение произвольной формы, контур которого с достаточной степенью точности может быть представлен отрезками ломаных прямых. Вводим правую пря­моугольную систему координат ОХYZ таким образом, чтобы контур рассматриваемого поперечного сечения лежал в плоскости ХОУ, рис.1. На котором показан случай, когда между точками контура 7 и 11 исходная кривая второго порядка /пунктир на рис. I/ заменена набором прямых. При увеличении числа точек излома прямых точность такой аппроксимации, естественно, воз­растает.

В принятой системе координат задает координаты всех точек излома контура. Данные точки нумеруем от 1 до m, начиная с некоторой произвольной точки, обходя контур сечения против движения часовой стрелки. При этом первая и последняя т точки излома контура совпадают, то есть значение m на единицу пре­вышает количество точек излома контура.

Обозначим через Хк, Yк_координаты К-той точки излома кон­тура, тогда вектор 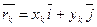соединяет начало коорди­нат с этой точкой контура. Вводим следующие обозначения [2]:

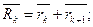
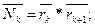
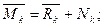
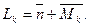(1)

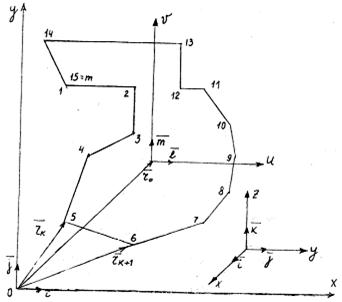
Рис.1

В формулах (1) 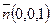- единичный вектор, перпендикулярный плоскости сечения. Из рассмотрения рис. 1 можно заключить, что площадь треугольника 0;К;К+1 равна модулю |DF| векторного произведения:

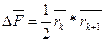(2)

При обходе всего контура сечения получим вектор [2]:

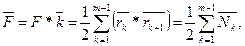(3)

модуль которого F равен площади сечения.

Вектор статического момента площади 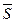равен [2]:

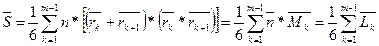(4)

Положение центра тяжести сечения определяется радиусом-вектором 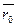, выходящим из начала координат и оканчивающимся в центре тяжести сечения [2] :

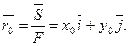(5)

Проекции x₀, у₀ вектора 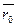на оси ОХ, ОY дают координаты центра тяжести сечения.

Вводим новую систему координат UV с началом в центре тя­жести сечения, оси U , V которой параллельны соответственно осям ОХ, ОY. Координаты точек излома контура в новой системе координат определяются радиусом-вектором 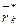[2] :

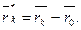(6)

Введем следующие обозначения [2] :

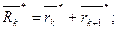
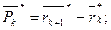
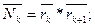(7)

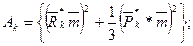
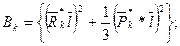
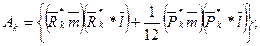
где 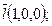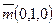-единичные векторы, направленные вдоль осей U , V .

С использованием обозначений (7) выражения для осевых Y_U, Y_V и центробежного Y_UV моментов инерции сечения относитель­но осей U , Y имеют вид [2]:

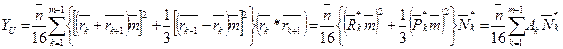(8)

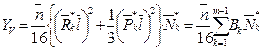
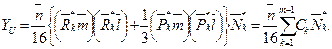
Значения главных центральных моментов инерции Y_max, Y_min и положение главных центральных осей инерции U’, V’ опреде­ляются по обычным формулам [1]:

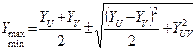(9)

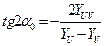(10)

Отметим, что на практике часто встречаются поперечные се­чения с отверстием. Для применения данной методики расчета к таким сечениям отверстие необходимо соединить разрезом с внеш­ним контуром сечения, рис.2.

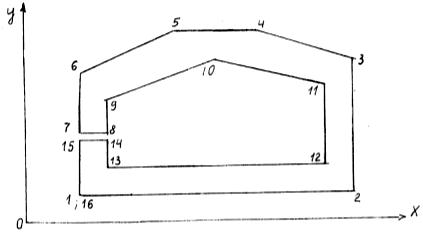
Рис.2

При этом получается единый контур сечения, для которого приме­нима изложенная выше методика определения геометрических ха­рактеристик плоских сечений.

Возможны повреждения в элементах конструкции, а именно ка­верны, сколы, выбоины, истирания, последствия технологических проливов кислот, масел и других агрессивных жидкостей и газов. В результате изменяется геометрия поперечного сечения повреж­денного элемента конструкции и после его натурного освидетель­ствования необходимо аппроксимировать отрезками ломаной прямой контур поврежденного сечения, рис.3.

При этом следует располагать точки излома контура несколько отодвинутыми от истинного контура сечения, так как материал в зоне дефекта часто повреждается на некоторую глубину d.

Если конструкция подвергается действию агрессивных сред, например, подвержена действию атмосферной коррозии, то необхо­дим учет изменения величин геометрических характеристик сече­ний во времени.

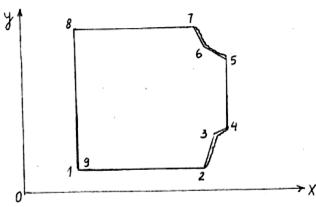
Рис.3

Считаем, что при наличии движения фронтов повреждения ма­териала поперечного сечения координаты точек на контуре сече­ния с течением времени меняется. Если задать скорость движения W_k/мм/год/, направление движения α_k /градусы/(0≤α_k≤360º) .число прошедших лет H, то новые координаты точки "К" можно вычислить по формулам:

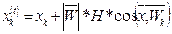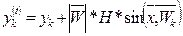, . (11)

При этом изложенная выше методика расчета используется для требуемых моментов времени H=H₁, H₂,…., H_N.

Определение критического времени Нк производится путем сопоставления величин геометрических характеристик F_i, S_xi, S_yi, J_xi, J_yi cминимально допустимыми для данного элемен­та конструкции. Кроме того, может использоваться условие о не­допустимости чрезмерного утонения конкретной части профиля.

Очевидно, что, не дожидаясь окончания срока H* , необхо­димо или усилить данный элемент конструкции, или заменить его на новый элемент.

Если же скорость движения фронтов повреждений изменяется с течением времени, то необходимо взять в формулах (11) за ис­ходные величины x_k, y_k значения на момент изменения скорос­тей и вновь использовать формулы (11) и всю методику расчета.

В табл.1 приведены скорости движения коррозии для различных типов агрессивности среды, там же приведены показатели снижения прочности материала.

Таблица 1

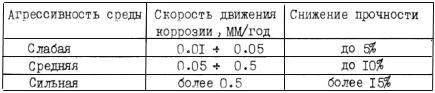
Отметим также, что по касте атмосферной коррозии для г. Саратова скорость берется от 20 до 24 МКМ/год, а для Прибал­тики- 43 МКМ/год, что соответствует 0.043 ММ/год и определяется близостью к морской соленой воде, ускоряющей коррозию.