Знаходження частинного розв’язку лінійно неоднорідного диференціального рівняння методом невизначених коефіцієнтів

Для деяких частинних випадків функції 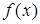можна знайти частинні розв’язки диференціального рівняння (5.26) без квадратур.

I). Розглянемо диференціальне рівняння з правою частиною

, (5.37)

де поліном з дійсними чи комплексними коефіцієнтами, -постійне дійсне чи комплексне число.

Розглянемо два випадки.

Випадок 1. Число не є коренем характеристичного рівняння. Тоді частинний розв’язок диференціального рівняння (5.37) шукають у вигляді

, (5.38)

де

(5.39)

поліном 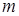-ої степені з невизначеними коефіцієнтами. Тобто, в цьому випадку частинний розв’язок має ту ж аналітичну структуру, що і права частина диференціального рівняння (5.37)

Коефіцієнти знаходяться шляхом підстановки (5.38) в (5.37) і прирівнювання коефіцієнтів при однакових степенях .

Переконаємося, що шукані коефіцієнти визначаються однозначно. Підставимо (5.38) в (5.37), отримаємо

Використовуючи вищенаведені формули, запишемо

.

На основі них маємо

Скорочуємо на і прирівнюємо коефіцієнти при однакових степенях

(5.40)

Так як , то з (5.40) послідовно визначаються всі коефіцієнти .

Випадок 2. Параметр являється 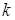-кратним коренем характеристичного рівняння , тобто

. (5.41)

В цьому випадку частинний розв’язок не можна побудувати в вигляді (5.38), так як . Його шукаємо у вигляді

, (5.42)

де – поліном вигляду (5.39).

Коефіцієнти полінома визначаються шляхом підстановки (5.42) в (5.37).

Звідки

.

Прирівнюємо коефіцієнти при однакових степенях

(5.43)

З (5.43) послідовно однозначно визначаються , так як .

II). Припустимо, що права частина диференціального рівняння (5.26) має вигляд

, (5.44)

де , – відомі поліноми степені менше або рівне 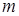(хоча б один має степінь ).

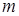Використовуючи формули Ейлера, обчислимо

і перепишемо функцію 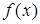таким чином

де і – поліноми степені 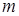, тобто 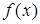є сума двох функцій, які розглянуті вище.

Випадок 1. Число не є коренем характеристичного рівняння. Тоді частинний розв’язок шукаємо у вигляді

, (5.45)

де і – поліноми 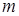-ої степені з невизначеними коефіцієнтами.

Випадок 2. Якщо – 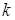-кратний корінь характеристичного рівняння, то частинний розв’язок шукаємо в вигляді

. (5.46)

Приводячи (5.45) і (5.46) до дійсного вигляду, сформулюємо наступне правило знаходження частинного розв’язку для випадку (5.44).

Випадок 1. Якщо не є коренем характеристичного рівняння, то

. (5.47)

Випадок 2. Якщо – 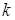-кратний корінь характеристичного рівняння ( ), то

. (5.48)

Тут і – поліноми 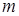-ої степені з невизначеними коефіцієнтами.

Приклад 5.12. Знайти загальний розв’язок диференціального рівняння методом невизначених коефіцієнтів

.

Розв'язання. Запишемо розв’язки однорідного диференціального рівняння

, , , .

Знаходимо розв’язки неоднорідного диференціального рівняння

, , ,

, .

Отже

– загальний розв’язок.

Приклад 5.13. Знайти загальний розв’язок диференціального рівняння методом невизначених коефіцієнтів

.

Розв'язання. , , , .

Так як – корінь кратності ,то

, ,

– загальний розв’язок.

Приклад 5.14. Знайти загальний розв’язок диференціального рівняння методом невизначених коефіцієнтів

. .

Розв'язання. Для нашого випадку .

Маємо , , , .

Оскільки , то . Після підстановки отримаємо

,

– загальний розв’язок.

5.3. Неоднорідні лінійні диференціальні рівняння n-го порядку

5.3.1. Структура загального розв¢язку неоднорідного рівняння

Розглянемо неоднорідне диференціальне рівняння

, (5.49)

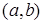де – неперервні на функції.

Припустимо, що для диференціального рівняння (5.49) ми знайшли частинний розв¢язок так, що

. (5.50)

Введемо нову змінну

. (5.51)

Тоді

.

Звідки

. (5.52)

Диференціальне рівняння (5.52) називається однорідним диференціальним рівнянням, яке відповідає неоднорідному диференціальному рівнянню (5.49).

Загальний розв¢язок диференціального рівняння (5.52) записується у формі

, (5.53)

де – фундаментальна система розв'язків диференціального рівняння (5.52), – довільні сталі. Тоді

(5.54)

буде загальним розв¢язком диференціального рівняння (5.49) в області

. (5.55)

Таким чином, для знаходження загального розв¢язку неоднорідного диференціального рівняння (5.49) необхідно знайти один частинний розв¢язок диференціального рівняння (5.49) і прибавити до нього загальний розв¢язок однорідного диференціального рівняння.

Зауваження 5.1. Розглянемо диференціальне рівняння

. (5.56)

Припустимо, що – частинний розв¢язок диференціального рівняння , а – частинний розв¢язок диференціального рівняння . Тоді, очевидно, – частинний розв¢язок диференціального рівняння (5.56).

Приклад 5.15. Знайти частинний розв¢язок диференціального рівняння

.

Розв'язання. Розглянемо диференціальні рівняння:

a) для якого ;

b) для якого .

Тоді – частинний розв¢язок даного диференціального рівняння.

5.3.2. Метод варіації довільної сталої (метод Лагранжа)

Загальний розв¢язок неоднорідного диференціального рівняння(5.49) можна знайти в квадратурах, якщо відомо загальний розв¢язок відповідного однорідного диференціального рівняння (5.52). Будемо шукати загальний розв¢язок диференціального рівняння (5.49) у вигляді

, (5.57)

де – деяка фундаментальна система розв¢язків диференціального рівняння (5.52).

Виберемо функції так, щоб функція (5.57) була загальним розв¢язком диференціального рівняння (5.49). Так як шукані функції задовольняють тільки одній умові, то для їх визначення можна підпорядкувати їх будь яким (n-1) умовам.

Таким чином, знайдемо n похідних функції (5.57):

;

й покладемо ;

й покладемо; ;

………………..

й покладемо ;

й покладемо .

Підставляючи (5.58) в диференціальне рівняння (5.49) отримаємо n –е рівняння

.

Таким чином, для визначення невідомих функцій отримаємо систему диференціальних рівнянь

. (5.59)

Відносно – це система лінійних рівнянь з визначником . Для знаходження запишемо формулу

, (5.60)

де – алгебраїчне доповнення до елементу n-го рядка і i –го стовпчика визначника . Всі функції, які входять в праву частину диференціального рівняння (5.60) є неперервними на 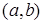. З (5.60) отримаємо

, (5.61)

де – довільні сталі, .

Тоді загальний розв¢язок диференціального рівняння (5.49) запишеться у вигляді

. (5.62)

Тут

(5.63)

– частинний розв¢язок диференціального рівняння (5.49).

Неважко перевірити, що частинний розв¢язок (5.63) задовольняє нульовим початковим умовам

.

Приклад 5.16. Знайти загальний розв¢язок диференціального рівняння

.

Розв'язання. Фундаментальна система розв¢язків для диференціального рівняння буде . Отже

.

Тому загальний розв¢язок запишемо у вигляді ( )

,

.

Зокрема, для диференціального рівняння другого порядку

(5.64)

загальний розв¢язок запишеться у вигляді

. (5.68)

При цьому – частинний розв¢язок диференціального рівняння (5.64), який задовольняє цьому рівнянню з початковими умовами , .

Для диференціального рівняння виду

, (5.66)

так як , що випливає з формули Остроградського – Ліувілля, загальний розв¢язок запишемо у формі

. (5.67)

Таким чином, для знаходження загального розв¢язку диференціального рівняння (5.49) необхідно знайти фундаментальну систему розв¢язків однорідного рівняння (5.52), після чого загальний розв¢язок запишеться в квадратурах.

5.3.3. Знаходження частинного розв¢язку лінійного неоднорідного диференціального рівняння n –го порядку методом Коші

Припустимо, що для рівняння (5.52) відома фундаментальна система розв¢язків . Використовуючи (5.53), побудуємо частинний розв¢язок диференціального рівняння (5.52), який задовольняє початковим умовам

. (5.68)

Цей розв¢язок буде залежати від , як від параметра . Тут , функція має неперервні частинні похідні по та до n –го порядку включно. Причому, вона є розв¢язком диференціального рівняння (5.52) . Крім цього, в силу початкових умов (5.68), функція задовольняє умовам

, (5.69)

де

.

Умову (5.69) можна записати і так

, (5.70)

де

.

Розглянемо функцію

, (5.71)

де і покажемо, що ця функція є частинним розв¢язком диференціального рівняння (5.49) з початковими умовами

.

Для цього використаємо формулу

.

Знаходимо похідні

,

,

………………………… (5.72)

,

.

Підставимо (5.72) в диференціальне рівняння (5.49), отримаємо

.

Тобто , а це означає, що функція (5.71) є частинним розв¢язком диференціального рівняння (5.49). Формула (5.71) називається формулою Коші.

5.4. Лінійні диференціальні рівняння n –го порядку зі змінними коефіцієнтами, які зводяться до рівнянь з постійними коефіцієнтами

a). Рівняння Ейлера

Це рівняння вигляду

. (5.73)

Це рівняння приводиться до рівняння з постійними коефіцієнтами заміною

. (5.74)

Дійсно

,

, (5.75)

……………………

.

Підставляючи (5.74) і (5.75) в диференціальне рівняння (5.73) ми отримаємо диференціальне рівняння n-го порядку з постійними коефіцієнтами

. (5.76)

Частинні розв¢язки диференціального рівняння (5.76) знаходять у вигляді . Враховуючи (5.74), частинні розв¢язки диференціального рівняння (5.73) можна зразу шукати у вигляді (5.74)

. (5.77)

b). Рівняння Лагранжа має вигляд

. (5.78)

Це рівняння заміною також приводиться до диференціального рівняння з постійними коефіцієнтами.

c). Рівняння

(5.79)

називається рівнянням Чебишева і після заміни при воно набирає вигляду

. (5.80)

Дійсно

,

.

Отже

,

.

Тобто отримали (5.80).

Приклад 5.17. Розв¢язати диференціальне рівняння

.

Розв'язання. Випишемо і розв¢яжемо характеристичне рівняння

,

.

Тому фундаментальна система розв¢язків буде наступною

.

Отже

– загальний розв¢язок.

5.5. Деякі питання теорії лінійних однорідних диференціальних рівнянь другого порядку. Задача Штурма – Ліувилля