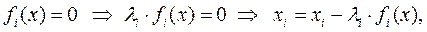Итерационные методы решения линейных алгебраических систем
Метод простой итерации или метод Якоби
матричный вид системы линейных уравнений:
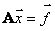 ,
,
где  ,
, 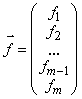 ,
, 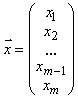 .
.
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:
 (1),
(1),
Теперь, задав нулевое приближение 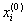 , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
, по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
 (2)
(2)
Аналогично находятся следующие приближения 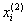 , где в (2) вместо
, где в (2) вместо 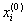 необходимо подставить
необходимо подставить 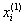 .
.
Или в общем случае:
 . (3)
. (3)
или 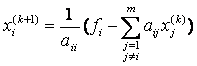
Условие окончания итерационного процесса- 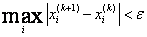 .
.
Достаточное условие сходимости:Если выполнено условие диагонального преобладания, т.е. 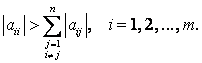 , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
, то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут 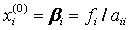 или
или 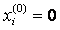 .
.
Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.
Алгоритм метода простых итераций
1. Преобразовать систему 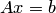 к виду
к виду 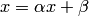 одним из описанных способов.
одним из описанных способов.
2. Задать начальное приближение решения 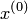 произвольно или положить
произвольно или положить 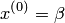 , а также малое положительное число
, а также малое положительное число  (точность). Положить
(точность). Положить 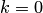 .
.
3. Вычислить следующее приближение 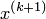 по формуле
по формуле 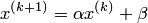 .
.
4. Если выполнено условие 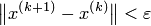 , процесс завершить и в качестве приближенного решения задачи принять
, процесс завершить и в качестве приближенного решения задачи принять 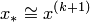 . Иначе положить
. Иначе положить 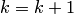 и перейти к пункту 3 алгоритма.
и перейти к пункту 3 алгоритма.
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
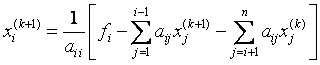
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:
Алгоритм метода Зейделя
1. Преобразовать систему 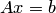 к виду
к виду 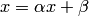 одним из описанных способов.
одним из описанных способов.
2. Задать начальное приближение решения 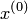 произвольно или положить
произвольно или положить 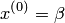 , а также малое положительное число
, а также малое положительное число  (точность). Положить
(точность). Положить 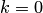 .
.
3. Произвести расчеты по формуле (1)или (2) и найти 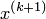 .
.
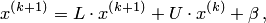 (2)
(2)
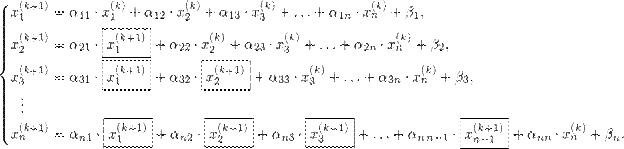 (1)
(1)
4. Если выполнено условие окончания 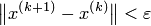 , процесс завершить и в качестве приближенного решения задачи принять
, процесс завершить и в качестве приближенного решения задачи принять 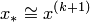 . Иначе положить
. Иначе положить 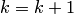 и перейти к пункту 3.
и перейти к пункту 3.
Достоинства итерационных методов:
1. Погрешность округления не накапливается от итерации к итерации.
2. Число итераций при n>100 обычно меньше n , поэтому общее число действий меньше n3, т.е. меньше, чем в методе исключений Гаусса.
3. Не требуется больший объем памяти.
4. Итерационные методы особенно выгодны для систем с большим количеством нулевых коэффициентов (систем с разряженной итерацией). Методы исключения наоборот: чем больше нулей, тем чаще требуется выбирать новую рабочую строку.
Недостаток - не всегда можно обеспечить сходность итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.
11.)
Нормы векторов
Определение.Пусть имеется n - мерное метрическое пространство вещественных чисел 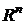 . Если для любого вектора . Если для любого вектора 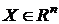 существует число существует число 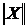 такое, что: 1) такое, что: 1) 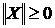 , причем , причем 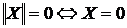 ; 2) ; 2) 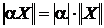 , где aÎR; 3) , где aÎR; 3) 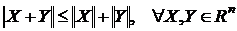 , - неравенство треугольника; то , - неравенство треугольника; то 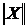 называется нормой вектора X. называется нормой вектора X. |
При решении СЛАУ наиболее распространены следующие нормы:
1. max-норма, или m – норма: 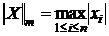 ;
;
2. l-норма: 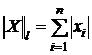 ;
;
3. Евклидова норма: 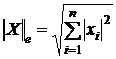 .
.
Определение.Пусть X* – точное значение вектора, X ‑ приближенное значение. Абсолютная и относительная погрешность вектора X*: 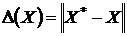 , , 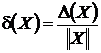 . . |
Пример:
Вычислим нормы вектора 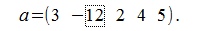
1. m-норма: 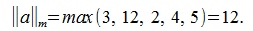
2. l-норма: 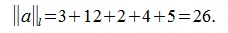
3. Евклидова норма: 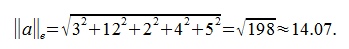
12.)
Нормы матриц
Согласованные с нормами векторов нормы матрицы A равны
1. max-норма, или m - норма:
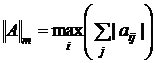 ; (normi(A) в Mathcad)
; (normi(A) в Mathcad)
2. l-норма:
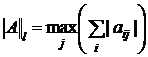 ; (norm1(A) в Mathcad)
; (norm1(A) в Mathcad)
3. Евклидова норма:
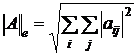 . (norme(A) в Mathcad)
. (norme(A) в Mathcad)
Свойства норм матриц.
1) 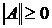 , причем
, причем 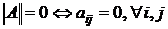 ;
;
2) 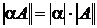 , где aÎR;
, где aÎR;
3) 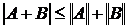 ;
;
Дополнительно верны следующие свойства:
4) 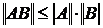 ;
;
5) 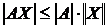 , здесь X – вектор.
, здесь X – вектор.
Как и для векторов, для матриц можно определить понятие погрешности.
Определение.Пусть A* – точное значение матрицы, A ‑ приближенное значение. Абсолютная и относительная погрешность матрицы A*: 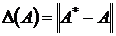 , , 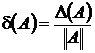 . . |
Пример: Пусть
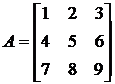 .
.
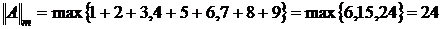 ;
;
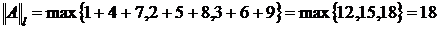 ;
;
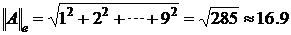 .
.
13.)
Метод простых итераций, реализующийся в процессе последовательных приближений, сходится к единственному решению исходной системы 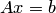 при любом начальном приближении
при любом начальном приближении 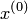 со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы
со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы 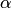 меньше единицы, т.е.
меньше единицы, т.е. 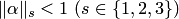 .
.
1. Условие теоремы, как достаточное, предъявляет завышенные требования к матрице 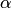 , и потому иногда сходимость будет, если даже
, и потому иногда сходимость будет, если даже 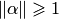 .
.
2. Сходящийся процесс обладает свойством "самоисправляемости", т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать, как новое начальное.
3. Условия сходимости выполняются, если в матрице  диагональные элементы преобладают, т.е.
диагональные элементы преобладают, т.е.
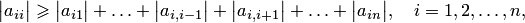
и хотя бы для одного  неравенство строгое. Другими словами, модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов (свободные члены не рассматриваются).
неравенство строгое. Другими словами, модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов (свободные члены не рассматриваются).
4. Чем меньше величина нормы 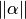 , тем быстрее сходимость метода.
, тем быстрее сходимость метода.
Теорема о необходимом и достаточном условии сходимости метода простых итераций. Для сходимости метода простых итераций (10.12) при любых 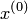 и
и 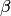 необходимо и достаточно, чтобы собственные значения матрицы
необходимо и достаточно, чтобы собственные значения матрицы 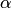 были по модулю меньше единицы, т.е.
были по модулю меньше единицы, т.е. 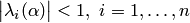 .
.
Преобразование системы 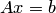 к виду
к виду 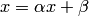 с матрицей
с матрицей 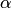 , удовлетворяющей условиям сходимости, может быть выполнено несколькими способами. Алгоритм:
, удовлетворяющей условиям сходимости, может быть выполнено несколькими способами. Алгоритм:
1. Уравнения, входящие в систему 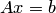 , переставляются так, чтобы выполнялось условие преобладания диагональных элементов (для той же цели можно использовать другие элементарные преобразования). Затем первое уравнение разрешается относительно
, переставляются так, чтобы выполнялось условие преобладания диагональных элементов (для той же цели можно использовать другие элементарные преобразования). Затем первое уравнение разрешается относительно 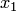 , второе — относительно
, второе — относительно 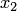 и т.д. При этом получается матрица
и т.д. При этом получается матрица 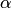 с нулевыми диагональными элементами.
с нулевыми диагональными элементами.
Выражая 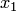 из первого уравнения,
из первого уравнения, 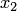 — из второго, а
— из второго, а 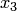 — из третьего, получаем систему вида
— из третьего, получаем систему вида 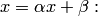
2. Уравнения преобразуются так, чтобы выполнялось условие преобладания диагональных элементов, но при этом коэффициенты 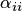 не обязательно равнялись нулю.
не обязательно равнялись нулю.
3. Если 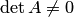 , систему
, систему 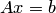 следует умножить на матрицу
следует умножить на матрицу 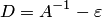 , где
, где 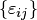 — матрица с малыми по модулю элементами. Тогда получается система
— матрица с малыми по модулю элементами. Тогда получается система 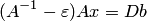 или
или 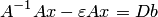 , которую можно записать в форме
, которую можно записать в форме 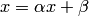 , где
, где 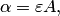
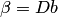 . Если
. Если 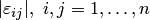 достаточно малы, условие сходимости выполняется.
достаточно малы, условие сходимости выполняется.
В методе простой итерации если аii 0, то исходная система может быть преобразована к виду хi = bi + aij хj , i j, т.е. из каждого уравнения последовательно выражают хi.
Здесь bi = Fi / аii; aij = - аij / аii.
Таким образом, в матричном виде имеем Х = В+ AХ.
Полученную систему будем решать методом последовательных приближений.
За нулевое приближение Х(0)можно принять матрицу В:Х(0)= = B, и далее, подставив найденные значения в исходную систему, получим
Х (1) = В + A Х(0) .
При бесконечном повторении этой вычислительной схемы имеем
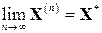 , где
, где 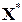 и будет искомое решение системы.
и будет искомое решение системы.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут 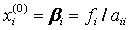 или
или 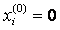 .
.
14.)
Итерационные методы решения линейных алгебраических систем: (основанны на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений.)
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
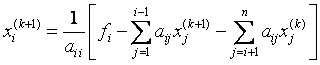
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:
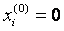
Алгоритм метода Зейделя
1. Преобразовать систему 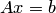 к виду
к виду 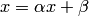 одним из описанных способов.
одним из описанных способов.
2. Задать начальное приближение решения 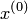 произвольно или положить
произвольно или положить 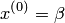 , а также малое положительное число
, а также малое положительное число  (точность). Положить
(точность). Положить 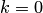 .
.
3. Произвести расчеты по формуле (1)или (2) и найти 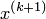 .
.
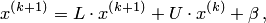 (2)
(2)
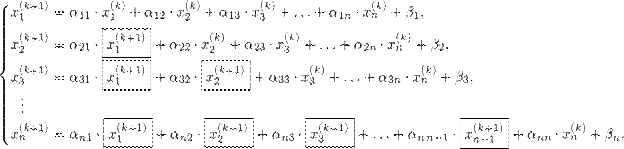 (1)
(1)
4. Если выполнено условие окончания 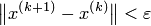 , процесс завершить и в качестве приближенного решения задачи принять
, процесс завершить и в качестве приближенного решения задачи принять 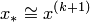 . Иначе положить
. Иначе положить 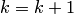 и перейти к пункту 3.
и перейти к пункту 3.
15.)
Решение систем нелинейных уравнений (СНУ).
Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:
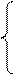 f1(x1, x2, …, xn) = 0
f1(x1, x2, …, xn) = 0
f2(x1, x2, …, xn) = 0 (5.1)
…
fn(x1, x2, …, xn) = 0
Эту систему можно записать в компактной, операторной форме:
F(X) = 0 (5.2)
где
|
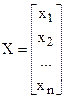
|
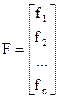
Решением системы называется набор значений 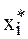 ,
, 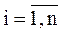 (вектор X*), при которых все функции fi равны 0 (система (5.1) обращается в тождество.)
(вектор X*), при которых все функции fi равны 0 (система (5.1) обращается в тождество.)
СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:
1 этап – отделение решений.
2 этап – уточнение всех или только нужных решений.
Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным.
Задача отделения решений достаточно просто решается только для системы двух уравнений с двумя неизвестными.
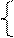 f1(x1, x2) = 0
f1(x1, x2) = 0
f2(x1, x2) = 0
Для этого необходимо в координатах (x1, x2) построить кривые
f1(x1,х2) = 0, f2(x1,х2) = 0.
Точки пересечения этих кривых являются решениями системы. Так как координаты точек пересечения определяются приближенно, целесообразно говорить об области существования решения D. Эта область задается интервалами по каждой координате, внутри которых находятся искомые значения неизвестных.
 |
Графическое отделение решений СНУ.
Для систем с большим числом неизвестных (n ³ 3) удовлетворительных общих методов определения области существования решения нет. Поэтому при решении СНУ эта область обычно определяется при анализе решаемой задачи, например, исходя из физического смысла неизвестных.
Отделение решений позволяет:
- Выявить число решений и область существования каждого из них.
- Проанализировать возможность применения выбранного метода решения СНУ в каждой области.
- Выбрать начальное приближение решения X(0) из области его существования, так что X(0)ÎD.
При отсутствии информации об области существования решения СНУ выбор начального приближения X(0) проводиться методом проб и ошибок (методом “тыка”).
Постановка задачи.
Требуется решить систему нелинейных уравнений 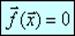 . В координатном виде эту задачу можно записать так:
. В координатном виде эту задачу можно записать так: 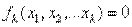 , где 1 ≤ k ≤ n.
, где 1 ≤ k ≤ n.
Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.
16.)
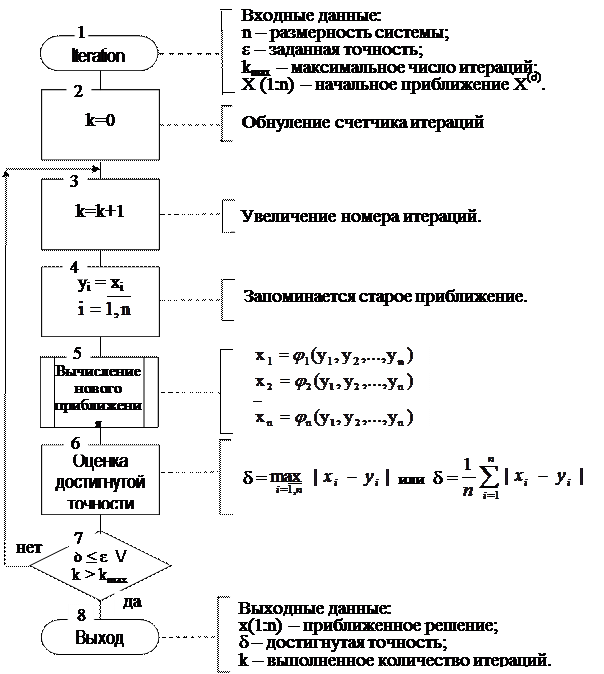
Метод простых итераций.
Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений
 f1(x1, x2, …, xn) = 0
f1(x1, x2, …, xn) = 0
f2(x1, x2, …, xn) = 0
…
fn(x1, x2, …, xn) = 0 (5.1)
эквивалентной системой X=Φ(X) –(5.3) и построении итерационной последовательности
(5.4)-X(k) = Φ(X(k-1)) , где k=1,2,3,… - номер итерации,которая при k→∞ сходится к точному решению.
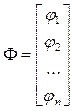 Здесь - итерирующая вектор-функция, X(0)
Здесь - итерирующая вектор-функция, X(0)  D – начальное приближение решения.
D – начальное приближение решения.
В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:
xi.(k) = φi(x1(k-1), x2(k-1), … , xn(k-1)), 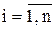 . (5.5)
. (5.5)
Условие окончания расчета
δ≤ε (5.6)
где ε - заданная точность решения;
δ = 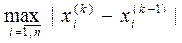 (5.7)
(5.7)
или
δ = 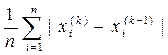 (5.8)
(5.8)
Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:
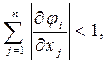
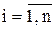 (5.9)
(5.9)
или
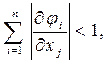
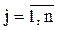 (5.10)
(5.10)
Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).
В простейшем случае эквивалентную систему можно получать как:
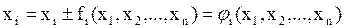 ,
, 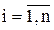
Можно выделить (не обязательно явно) все неизвестные из уравнений системы так, что:
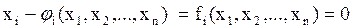 ,
, 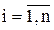
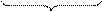 Как и в случае одного уравнения задачу поиска эквивалентного преобразования можно свести к задаче определения (в простейшем случае подбора) значений констант li ≠ 0,
Как и в случае одного уравнения задачу поиска эквивалентного преобразования можно свести к задаче определения (в простейшем случае подбора) значений констант li ≠ 0, 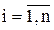 , обеспечивающих сходимость
, обеспечивающих сходимость