Графические модели некоторых пространственных кривых и их изобразительные свойства
12.7.1 Комплексный чертёж цилиндрической винтовой линии
(рис.12.53)
Так как цилиндрическая винтовая линия а принадлежит поверхности фронтально-проецирующего цилиндра Ф, то её фронта-льная проекция а2 совпадает с вырожден-ной в окружность проекцией Ф2 этой поверх-ности, а её горизонтальная проекция а1, по-строение которой графически моделирует процесс её образования, представляет собой один период синусоиды.
Цилиндрическая винтовая линия явля-ется пространственной кривой одинакового ската, так как касательные во всех её точках равнонаклонены к плоскости основания её цилиндра.
Отсюда следует, что на прямоугольнике развертки боковой поверхности цилиндра Ф винтовая линия будет выглядеть как его ди-агональ или гипотенуза прямоугольного тре-угольника, длина прилежащего катета кото-рого равна длине окружности основания цилиндра, а противолежащий катет равен шагу винта.
Угол j° между гипотенузой этого треу-гольника и прилежащим катетом называется углом подъёма винта, а длина гипотенузы называется витком цилиндрической гелисы.
Так как сечения цилиндра Ф соприка-сающимися плоскостями есть конгруэнтные эллипсы, то, определив для одного из них значение радиусов А0ОА и В0ОВ в точках А и В как концах его малой оси, откладываем эти значения на П2 по радиальным напра-влениям от точек проекции а2 и получаем фронтальную проекцию е2 эволюты гелисы в виде окружности
Горизонтальная проекция е1 этой линии является синусоидой, ортогонально сопря-
женной с синусоидой а1, так как в точках А1 и 41 их пересечения проекция b1 бинормали
b, перпендикулярная к t1, является карате-льной к е1 и наоборот.
Правила графического моделирования
цилиндрических винтовых линий применя- ются при проектировании различного вида
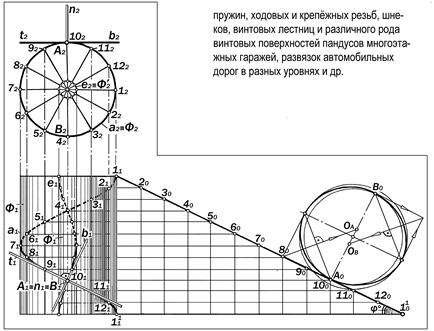 |
Рис.12.53. Графическая модель цилиндрической винтовой линии
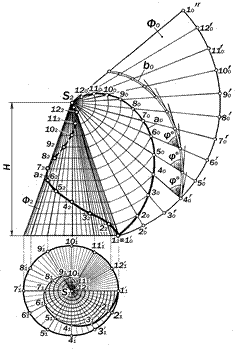 |
Рис.12.54.Графическая модель конической винтовой линии
12.7.2. Комплексный чертёж конической винтовой линии (рис. 12.54)
Принцип построения чертежа конической винтовой линии остаётся таким же, как и цилиндрической винтовой линии.
В результате её горизонтальной проек-цией является спираль Архимеда, а фрон-тальной – «затухающая синусо-ида»(рис.12.54).
На развёртке Ф0 поверхнос-ти конуса Ф коническая гелиса
выглядит как дуга спирали Ар-химеда, так как, начиная от вер-шины, каждая последующая её точка смещается относительно предыдущей на постоянную ве-личину в 1/12 часть длины об-разующей, последовательные положения которой смещаются при этом на 1/12 часть длины окружности основания.
Если на развертке поверх-ности конуса вычертить логами-фмическую спираль b0, пересе-кающую развертки образующих под постоянным углом j°, а затем свернуть развёртку в коническую поверхность, то эта спираль преобразуется в кони-ческую винтовую линию одина-кового ската.
Горизонтальной проекцией этой линии будет логарифмическая спи-раль, а фронтальной – затухающая сину-соида.
Конические гелисы применяются при проектировании различных шнеков, буров, режущих инструментов, шурупов и др.
Комплексные чертежи пространственных кривых линий на сферических поверхностях
12.7.3. Комплексный чертёж локсодромии
(рис. 12.55)
Графическое моделирование локсо-дромии или сферической винтовой линии следует начинать с построения её го-ризонтальной проекции в виде логариф-мической спирали вида: [ 6]
l = tga× ln r,
r - радиус-вектор спирали,
l - долгота точки на сфере (считая
от какого-либо начального мери-
диана);
a - заданный угол между локсодро-
мией и меридианами.
Фронтальную проекцию локсодромии следует строить на основе правил графи-
ческого моделирования отношения
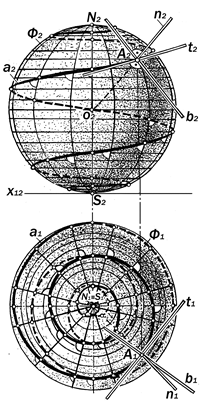 |
Рис. 12.55. Графическая модель сферической винтовой линии (локсодромии)
принадежности её точек к сферической поверхности. Представляет собой затуха-ющую к полюсам сферы кривую линию типа синусоиды.
Так как ортодромия или брахистохро-на является дугой окружности большого круга, то её ортогональными проекциямибудут дуги эллипсов ( см. п.12.5.2).
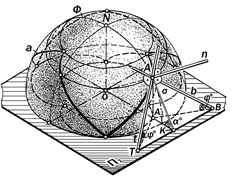 |
Рис.12.56.Геометрическая модель
сферической линии одинакового ската
на полусфере
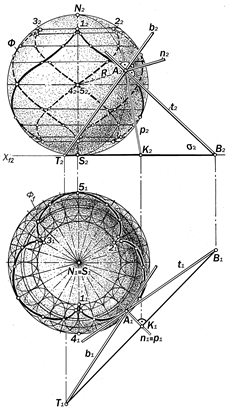 |
Рис.12.57. Графическая модель сферической линии одинакового ската
12.7.4. Комплексный чертёж сферической линии одинакового ската
(рис.12.57)
Графическое моделирование этой ли-нии (см. определение12.19, рис. 12.56) следует начинать с пост-роения её горизонтальной про-екции а1, представляющей со-бой рулетту - эпициклоиду (см рис.12.10), образующая точка которой расположена на под-вижной окружности-центроиде, радиус которой в три раза ме-ньше радиуса неподвижной центроиды.
Фронтальная проекция а2 этой линии строится на основе правил графического моделирования отно-шения принадлежности её точек к сфериче-ской поверхности.
В произвольной точке А ли-нии а одинакового ската нор-маль n имеет радиальное на-правление, а взаимно-перпен-дикулярные касательная t и би-нормаль b, продолженные до пересечения с плоскостью П1, образуют равнобедренный тре-угольник АВС спрямляющей плоскости s.
Линия одинакового ската сферы может быть принята за ребро возврата некоторой тор-совой поверхности, образующи-ми которой являются каратель-ные t.
В о п р о с ы
д л я п о в т о р е н и я:
1.Что называется кривой ли-нией?
2. Каков принцип образования кривой линии?
3. Какие кривые линии называются глад-кими?
4. Какими бывают особые точки кривых линий?
5. Какие линии называются касатель-ными и нормалями данной кривой линии?
6. Что такое кривизна кривой?
7. Какая линия называется эволютой дан- ной кривой и как она образуется?
8. Какие прямые и плоскости образуют
сопровождающий трёхгранник Френе для данной пространственной кривой?
9. Каковы системные определения окру-жности, эллипса, параболы и гиперболы?
10. Какие кривые линии называются ру-леттами?
11. Какова конструктивная пространст-венная природа фокусов и директрис-элли-псов, гипербол и парабол?
12. Каковы основные конструктивные свойства окружности, эллипса, гиперболы и параболы?
13. Какая линия называется подэрой дан-ной кривой относительно данной точки?
14. Какие точка и прямая относительно окружности называются соответственно по-люсом и полярой?
15. Какими конструктивными элемента-ми и как может быть задан эллипс?
16. При каких условиях эллипс можно назвать «золотым» и каковы его конструк-тивные свойства?
17. Как образовать гиперболу аппаратом центрального подвижного проецирования?
18. Как образовать эллипс и гиперболу при помощи подэры?
19. При каких условиях гиперболу можно назвать «золотой» и каковы её конструк-тивные свойства?
20. Каковы конструктивные свойства гра-фических композиций из золотых сопряжен-ных гипербол и золотых софокусных эллип-са и гиперболы?
21 .Какими конструктивными элемен-тами и как может быть задана гипербола?
22. При помощи какой подэры можно одновременно построить параболу и её эволюту?
23. Каковы изобразительные свойства ортогональных проекций окружности, элли-пса, гиперболы и параболы различных по-ложений в пространстве?
24. Какая линия называется цилиндри-ческой винтовой и каковы её конструк-тивные свойства?
25. Какая линия называется конической винтовой и каковы её конструктивные свойства?
26.Что собою представляют эволюты ци-линдрической и конической винтовых ли-ний?
27. Какие линии на сфере называются её параллелями, меридианами, ортодромией и локсодромией?
28. Каковы изобразительные свойства ортогональных проекций цилиндрической и конической винтовых линий?
29. Каковы изобразительные свойства ортогональных проекций локсодромии и сферической линии одинакового ската?
