Свойства решений системы линейных однородных уравнений. Теоремы о связи между решениями однородных и неоднородных систем

а₁₁х₁+ а₁₂х₂+...+ а_1nх_n=0 Однородная сист. всегда совместна. 0=х₁=х₂=...=х_n – тривиальная. Если r=n, то тревиальное

…………………………. решение будет ед. Если r<n, то сист. имеет параметрыбесконечное множество среди которых

а_s1х₁+ а_s2х₂+...+ а_snх_n=0 есть нулевые.

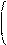
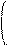
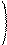
Св-ва реш. лин. однород. сист.:

__ b₁__ kb₁

1) Если в-р β= : , им реш. сист., то для любого числа k β = : также явл. решением.

__ __ b_n kb_n

2) Если β и γ – 2-а реш. сист., то их сумма также явл. решением.

1), 2) =>Любая линейная комбинация решение одной системы, также является решением.

Теоремы о связи между решениями однородных и неоднородных систем.

а₁₁х₁+ а₁₂х₂+...+ а_1nх_n=b₁ а₁₁х₁+ а₁₂х₂+...+ а_1nх_n=0

…………………………. – неоднород сист. …………………………. – привед. сист. соотв.

а_s1х₁+ а_s2х₂+...+ а_snх_n=b_s а_s1х₁+ а_s2х₂+...+ а_snх_n=0

Теорема1.

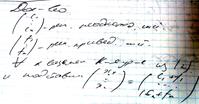
Сумма любого решения неоднородной системы с любым решением приведенной системы будет решением неоднородной системы.

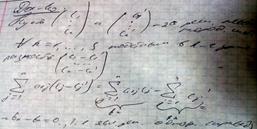Теорема2.

Разность любых 2-х решений неоднородной сист., явл. реш. привед. сист.

Теорема о числе решений фундаментальной системы решений.

Максимальная лнз сист. назыв. фундаментальной сист. реш.(фср).

Теорема(о числе решений входящих в ФСР)

Умножение матриц. Обратная матрица. Сумма матриц и умножение матрицы на число.

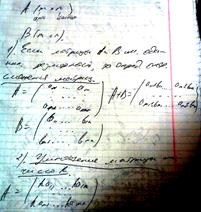
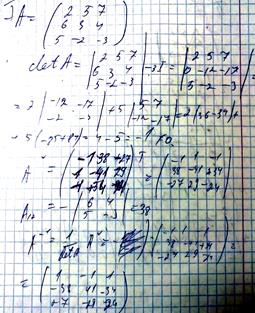
Линейное пространство. Определение, примеры.

Мн-во L наз. лин. пр-вом, а его элем. – векторами, если:

– заданна опер. сложение ₳ х є L x+y є L

– задана операция умножения вектора на действ. число. ₳ α є R, ₳ х є L , α x є L

– для этих операций справедливо 8 св-в ₳ х, y, z є L, ₳ α є R:

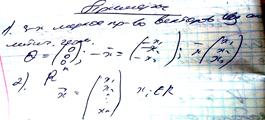
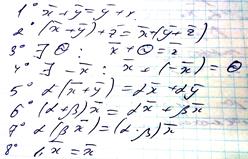
19) Теорема о линейной зависимости системы m векторов n-мерного пространства при m>n. Теорема о базисе n-мерного пространства.

В-ры х₁,..., х_n назыв. лин.зависимыми, если сущ. числа α₁,…, α_n которые (α₁²+…+ α_n²≠0): α₁х₁+…+ α_nх_n=0

В-ра х₁,..., х_n назыв. лин.независимыми, если из рав-ва α₁х₁+…+ α_nх_n=0 => α₁=…=α_n=0

Теорема.

В-ры х₁,..., х_n линейны <=>один из в-ров раскладыв. по остальным.

Базисом лин. пр-ва назыв. упорядоченная сист. в-ров, если она: – лнз; – любой в-р пр-ва по ней раскладывается.

Пример:

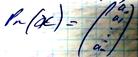L – мн-во многочленов от одной переменной, степень кот. не превосходит n.

P_n(x)=a₀+a₁x+ a₂x²+…+ a_nxⁿ. a_i є R. Линейное пр-во 1; x; x²;…;xⁿ – ЛНЗ.

α₀+ αх+ α₂х²+…+ α_nхⁿ ó α₀= α₁=…= α_n=0.

Любой многочлен P_n рассм. по этой сист. а корд.a₀, a₁,…, a_n.

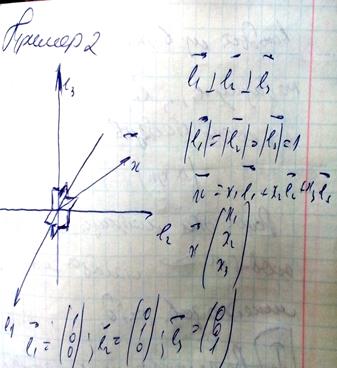
Лин. пр-во, в кот. сущ. базис из n-в-в, назыв. n-мерным пр-вом.

Число n – размерность пространства. n=dim(L)

В n-мерном пр-ве любая сист. из m в-ров линейнозависима, если m>n.

Док-во

Базис e₁, e₂,…,e_n. Рассм. f₁,..., f_m, m>n.

Каждый из в-в f_i разложим по базису e₁, e₂,…,e_n и сост. матрицу из корд. столбцов. (n x m). Ранг этой матрицы не превосходит n => столбцы матрицы линейнозав., чтд.

Теорема2.Теорема3.

В n-мерном пр-ве каждая упорядоченная сист.из n ЛНЗ В n-мерном пр-ве любую упорядоч. ЛНЗ сист.из k<n в-ров можно

в-в образует базис. доп. до базиса.

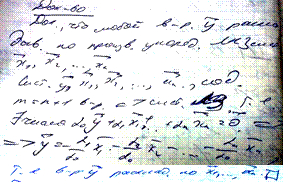
Замена базиса. Матрица перехода. Связь между координатами одного и того же вектора в разных базисах.

Матрица, столбцы кот. явл. корд. столбцами в-в е^/ в базисе е, наазыв. матрицей перехода от базиса е к базису е^/