Модели выпуклого программирования

Пусть дана система неравенств вида

j_i(x₁, x₂, ... , x_n) £ b_i , i=1,2,...,m (1)

x₁, x₂, ... ,x_n ³ 0,

и функция Z=f(x₁, x₂, ... , x_n), (2)

причем все функции j_i(Х) являются выпуклыми на некотором выпуклом множестве М, а функция Z либо выпукла на множестве М, либо вогнута.

Задача выпуклого программирования (ВП) состоит в отыскании такого решения системы ограничений (1), при котором целевая функция Z достигает минимального значения, или вогнутая функция Z достигает максимального значения.

Напомним, что множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий эти точки. Если [a,b] – отрезок на числовой прямой и хÎ[a,b], то х=aa+(1-a)b, 0£a£1 или

х=a₁a+a₂b, a₁+a₂=1, a₁³0, a₂³0. (*)

Нетрудно видеть и обратное: если выполняется (*), то хÎ[a,b].

Исходя из равенства (*) видно, что если М – выпуклое пространство, то 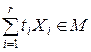для любых точек X₁,…,X_r ÎM и любых действительных чисел t_i ³0, удовлетворяющих условию .

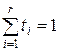Функция F(X)=F(x₁, x₂, ... , x_n), определенная на выпуклом множестве М n-мерного пространства, называется выпуклой на этом множестве, если

F(aX₁ +(1-a)X₂)£ aF(X₁ )+(1-a)F(X₂ ),

вогнутой на этом множестве, если F(aX₁ +(1-a)X₂)£ aF(X₁ )+(1-a)F(X₂ ),

строго выпуклой на этом множестве, если F(aX₁ +(1-a)X₂)> aF(X₁ )+(1-a)F(X₂ )

строго вогнутой на этом множестве, если F(aX₁ +(1-a)X₂)< aF(X₁ )+(1-a)F(X₂ ),

для любых точек Х₁, Х₂ ÎМ и любого числа aÎ[0,1].

Алгебраические и аналитические свойства выпуклых функций:

1. если функция F(X) выпукла, то функция - F(X) вогнута.
2. функция F(X)=С и линейная функция F(X)= aХ+b являются всюду выпуклыми и всюду вогнутыми.
3. если функции F_i(X), I=1,2,…,m выпуклы, то при любых действительных числах a_I³0 функция 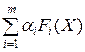также выпукла.
4. если функция F(X) выпукла, то для любого числа a область решений неравенства F(X)<a является выпуклым множеством, либо пустым.
5. если функции j_I(X) выпуклые при всех неотрицательных значениях переменных, то область решений системы неравенств j_I(X)£b_i, I=1,…,m является выпуклым множеством (если она не пуста).
6. выпуклая (вогнутая) функция, определенная на выпуклом множестве М, непрерывна в каждой внутренней точке этого множества.
7. всякая дифференцируемая строго выпуклая (вогнутая) функция имеет не более одной стационарной точки (т.е. точки, в которой равны 0 все частные производные). При этом для выпуклой (вогнутой) функции стационарная точка всегда является точкой локального и глобального минимума (максимума).
8. дважды дифференцируемая функция F(X)= F(x₁, x₂, ... ,x_n) является выпуклой в том и только в том случае, когда 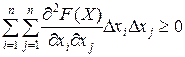для любых Х ÎМ и Dx_{i ,} Dx_j, не обращающихся в 0 одновременно.

Ввиду свойства 3 всякая ЗЛП является частным случаем задачи ВП. В общем случае задачи ВП являются ЗНП.

Выделение задач ВП в специальный класс объясняется экстремальными свойствами выпуклых функций:

- всякий локальный минимум выпуклой функции (локальный максимум вогнутой функции) является одновременно и глобальным;

- ввиду свойства 2 выпуклая (вогнутая) функция, заданная на замкнутом ограниченном множестве, достигает на этом множестве глобального максимума и глобального минимума.

Отсюда вытекает, что если целевая функция является строго выпуклой (строго вогнутой) и если область решений системы ограничений не пуста и ограничена, то ЗВП всегда имеет единственное решение. В этом случае минимум выпуклой (максимум вогнутой) функции достигается внутри области решений, если там имеется стационарная точка, или на границе этой области, если внутри нет стационарной точки.