Екінші peтті қисықтар жене олардың канондық теңдеулері

Жоғары математкада екінші дәрежелі теңдеулермен анықталатын сызықтарды екші pеттi қисықтар деп атайды. Олар негізінен шеңбер, эллипс, гипербола және парабола деп аталады. Бұл қисықтар техника мен ғылым саласында иі кездеседі.

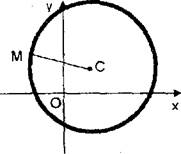
1. Шеңбер.Шеңбердеп аталатын берілген нүктеден бірдей қашықтықта жататын жазықтықтағы нүктелердің геометриялық орындарын шенбер деп атайды (8-сызба).

С(х₀,у₀) -берілген нукте. Шеңбердің бойынан кез келген

жылжымалы М(х,у) нүктесін алайык. Сонда СМ(х -х₀,у-у₀),

мұндағы F₁ және F₂ -фокус деп аталатын берілген 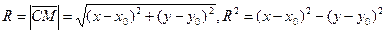центрі С нуктесінде жаткан радиусы R -ге тең шеңбердің канондық теңдеуі.

Егер шеңбердің центрі С координаттардың бас нүктесінде

жатса, онда х₀ = у₀ = 0 .

Сондыктан : х² +у² = R²

2. Эллипс.Фокустар деп аталатын берілген екі нүктеден қашықтықтарыньң қосындысы әрқашанда тұрақты шама болатын жазықтықтағы нұктелердің геометриялык орындарын эллипс деп атайды (9-сызба). Анықтама бойынша F₁M + F₂M = 2a

нүктелер,

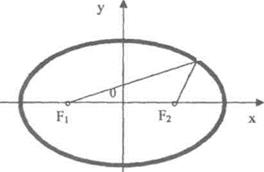М{х, у) -эллипстің бойындағы кез келген жылжымалы нүкте,

2а-тұрақты шама

Егер F₁F₂ = 2с десек, онда F₁(-C;0), F₂(C;0). Сонда:

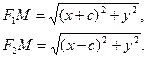
Енді осы мәндерді қойсақ:

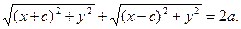
Немесе

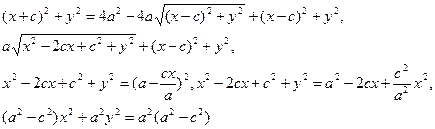
Егер а>с болса, онда а² —с²=b² болады. Сондықтан эллипстің канондық теңдеуі деп аталатын теңдеуге келеміз:

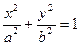
Мұндағы х пен у эллипстің кез келген жылжымалы нүктесінің координаттары, а -эллипстің үлкен жарты oci, b -онын кіші жарты oci.

Осьтер эллипске симметриялы, ал симметриялы осьтердің қиылысатын нуктесі эллипстің цeнтpi болады.

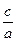қатынасын эллипстің эсцентриситеті деп атайды және оны 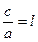деп белгілейді. Сонымен 6ipгe а > с болғандьқтан l < 1 немесе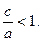

Эллипстің үлкен осіне перпендикуляр тузулердің ішінде 6ip түзудің эллипстің кші осінен қашықтықты d әрқашанда а/l қатынасына тең тұрақты шама болса, онда мұндай тузудіэллипстің директрисасы деп атайды. Директрисалардың тендеу 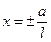.Эллипс үшін l < 1 болғандьқтан .

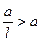Сондықтан эллипстің дериктрисалары оның сыртында жатады.

Егер a=b болса, онда шеңбер эллипстің дерпбес жағдайы болады. Бұл жағдайда с=0, ендеше шеңбердің эксцентриситеті нөлге тең.

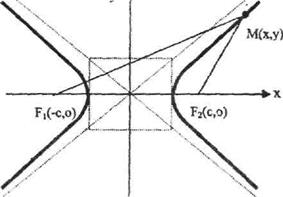
3. Гипербола.Фокустар деп аталатын берілген екі нүктеден
қашықтықтарының айырмасы әрқашанда тұрақты шама болатын
жазықтыктағы нүктелердің геометриялық орындарын гипербола деп атайды.

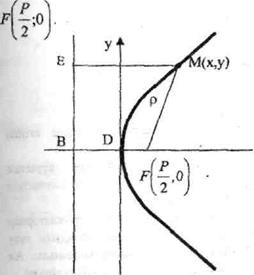
4. Парабола. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтарды нүктелерің геометриялык орындарын парабола дейді Берілген F нуктесінің координаталарын былай белгілейді

► *

Координаталардың бас нүктесінен Р/2 қашықтықтағы ординат осіне параллель берілген тузуді параболаның директрисасы дейді.

М(х,у) - параболаның бойындағы кез келген жылжымалы нүкте.

Анықтама бойынша

FM=ME

Екі нүктенің ара қашықтыгыньң формуласы бойынша

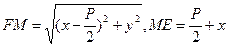
осы мәндерді апарып қойып, шыққан өрнекті түрлендірсек, параболаның канондық теңдеуі шығады:

у²=2рх

мұндагы р -берілген фокус пен директрисаның арасындағы қашықтық, х пен у - параболаның бойындағы кез келген жылжымалы нуктенің координатасы.

Параболаның эксцентриситеті: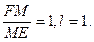

Параболаның директрисасының теңдеуі: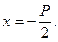

Екінші ретті беттер

Екінші ретті беттер деп, координаталар жүйесінде екінші дәрежелі теңдеулермен берілетін беттерді айтады.

Екінші ретті беттердің қасиеттері техникада, құрылыс негіздерінің конструкцияларында сонымен бірге күн сәулесінің қуатын от қуатына айналдыру мақсатында қолданылады.

Мысалы, шағылыстыру айналары, түрлі прожекторлар параболоидтың қасиеттеріне, ал бір қуысты гиперболоидтың түзу сызықты жасаушылары болу қасиеттерін құрылыста қолданады. Ал сфералық айналарды қолданып, өмірдің түрлі қажетіне пайдаланады.

1. Сфера.Бекрілген нүктеден бірдей қашықтықта орналасқан

кеңістіктегі нүктелердің геометриялық орындарын сфералық немесе шар беті деп атайды .

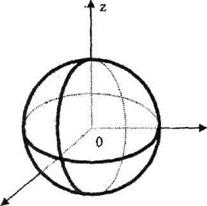
Егер сфераның центрі С(a,b,c) нүктесі және оның бетіндегі кез келген нүкте жылжымалы нүктесі M(x,y,z) болса, онда анықтама бойынша CM=R , R-сфераның радиусы.

Кеңістіктегі екі нүктенің арасындағы қашықтықтың формуласы бойынша

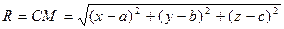немесе 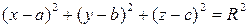- сфераның канондық теңдеуі.

Егер сфераның центрі координаталардың бас нүктесінде жатса, a=b=c=0. Сонда теңдеу мына түрдежазылады:

\

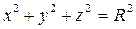
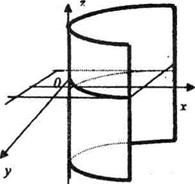
2.Цилиндр.Цилиндр перпендикулчрлық қимасындағы сызықтың түріне қарай төрт түрге бөлінеді: дөңгелек, эллипстік, гиперболалық, және парболалық цилиндр болып, осыған сәйкес цилиндр тік бұрышты координаталар жүйесінде төрт түрлі теңдеумен анықталады:

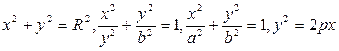
Бұл төрт теңдеу жазықтықта шеңберді, эллипсті, гиперболаны және паболаны кескіндейді, ал кеңістікте дөңгелек, эллипстік, гиперболалық және параболалық цилиндрлейді кескіндейді.

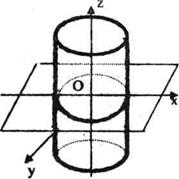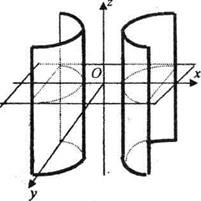
Сонымен цилиндр (цилиндрлік бет) дегеніміз шеңбер, элллипс, гипербола, параболалардың бойымен олардың жазықтықтарына перпендикуляр болып өтетін түзу сызықтардың үздіксіз қозғалысынан шығатын екінші ретті беттер.

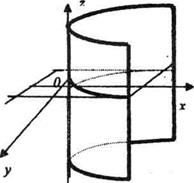Осы шеңбер, эллипс, гипербола, және парабола цилиндрлердің бағыттаушылары, ал цилиндрдің беттерінде жатқан түзулер олардың жасаушылары деп аталады.

3.Конус.Конус деп берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалысынан шығатын бетті айтады.

Конустың бағыттаушысы 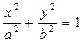эллипс, ал жасаушы түзуі координаталардың бас нүктесінен өтсін. Сонда конустың теңдеуі:

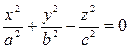болады.Мұндағы z=c конусты XOY жазықтығына параллель қиып өтетін жазықтық. Ал егер a=b болса, онда конустың перпендикулярлық қимасы шеңбер болады:

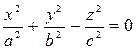- айнымалы концстың теңдеуі.

Егер a=b=c болса, онда мынандай конус шығады:

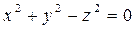
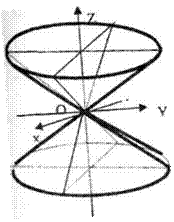Төбесі координаталардың бас нүктесінде апликата осіне симметриялы екінші ретті конустық беттің теңдеуі.

Дәл осындай қалған екі оське симметриялы конустық беттің теңдеулері мынандай болады:

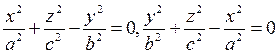
4.Айналу беттері. Егер кеңістікте бір сызық берілген осьті айналса, оның айналуынан бет п.б.

Айналушы сызықтың формасына байланысты бет әр түрлі болады. Мысалы, егер шеңбер өзінің диаметрі бойынша айналса, сфералық бет шығады, ал координаталар басынан өтетін түзу OZ осін айналса, дөңгелек конус п.б. Сызықтың айналатын осін айналу осі, ал пайда болған бетті айналу беті деп атайды.

Бізге YOZ жазықтығында жатқан L сызығы

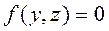
теңдеуімен берілсін. Осы сызықтың OY осін айналғанда пайда болған беттің теңдеуін табу үшін сол сызықтың 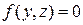теңдеудегі y – ті өзгертпей, z – ті 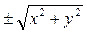өрнегімен алмастыру керек. Сонда айналу бетінің теңдеуі мынандай болады:

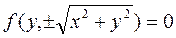
Басқа осьтерді айналғанда пайда болған беттердің де теңдеулері осыған ұқсас табылады. Яғни, егер берілген сызық OZ осінен айналса, онда айналу бетінің теңдеуі 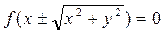болады.

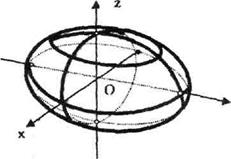
5. Айналу эллипсоиды. Үш осьті эллипсоид.YOZ жазықтығында 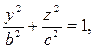теңдеулерімен берілген эллипсті OZ осімен айналдырғаннан шыққан бетті айналу эллипсоид деп атайды. Оның теңдеуі:

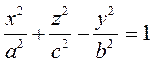
Егер b>c болса, онда қысыңқы, ал егер b<cболса, онда созыңқы айналу эллипсоид болады. Ал егер a=b=c болса, онда ол сфералық бет болады. Осы шыққан айналу эллипсоидты деформацияласақ, яғни

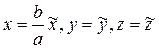десек, онда 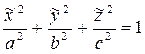шығады.(бұл үш осьті эллипсоидтың теңдеуі)

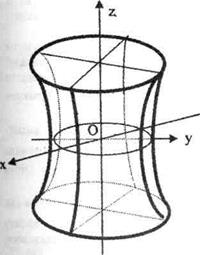
6. Бір қуысты гиперболоид. Бізге YOZ жазықтығында орналасқан гипербола 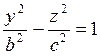теңдеуімен берілсін.

Осы гиперболаны OZ осінен айналдырсақ бір қуысты гиперболоид деп аталатын айналу беті шығады. Оның теңдеуі

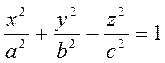болады.

Осы айналу гиперболоидын деформацияласақ, яғни

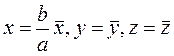десек, онда мына түрге келеді:

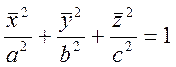
Осы теңдеумен анықталатын бетті бір қуысты гиперболоид деп атайды. Айнымалы бір қуысты гиперболоидтың бір қуысты гиперболоидтан айырмашылығы оның XOZ жазықтығына параллель жазықтықпен қимасы эллипс емес шеңбер болады.

7. Қуысты гиперболоид. Гиперболаның нақты осінен айналғаннан шығатын бетті екі қуысты гиперболоид деп атайды.

Егер XOZ жазықтығында жатқан 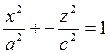; гиперболаны OX осінен айналдырсақ онда екі қуысты айналмалы гиперболоидтың теңдеуі былай жазылады:

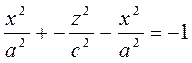
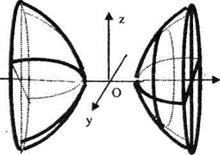Осы шыққан екі қуысты гиперболоидты деформацияласақ, онда осы түрге келеді:

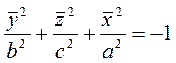(екі қуысты гиперболоидтың теңдеуі)

Екі қуысты айналмалы гиперболоидтың екі қуысты гиперболоидтан айырмашылығы оның YOZ жазықтығына параллель жазықтықпен қимасы шеңбер болады.

8. Айналу пороболоиды. Эллипстік параболоид.YOZ жазықтығында жатқан 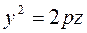параболаны OZ осінен айналдырғанда шығатын екінші ретті бетті айналмалы параболоид деп атайды. Оның теңдеуі былайжазылады:

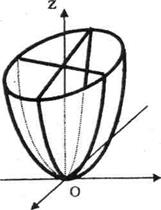
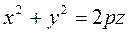
Шыққан айналу параболоидты деформацияласақ, яғни 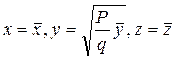десек, эллипстік параболоид деп аталатын екінші ретті беттік теңдеуі:

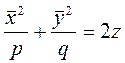шығады. Мұндағы p>0, q>0.

9. Гиперболалық параболоид. Егер эллипстік параболоидтың 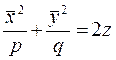теңдеуінің сол жағындағы екі мүшенің арасындағы таңбасын өзгертсек, яғни онда:

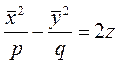
теңдеуіне келеміз. Мұндағы p>0, q>0.

Осы теңдеумен аеықталатын екінші бетті гиперболалық параболоид деп атайды.

Гиперболалық параболоидтың түрін анықтау үшін оның координат жазықтықтарымен және осы координат жазықтықтарына параллель жазықтықтарындағы қималарын қарастырамыз.

XOZ координат жазықтықтағындағы қимасы 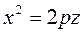парабола болады.

YOZ координат жазықтығындағы қимасы 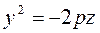парабола болады.

XOZ 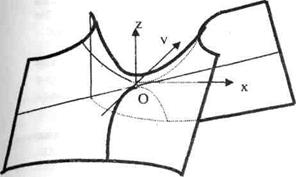координат жазықтықтағындағы қимасының теңдеуі

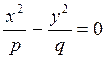болады.

Бұл теңдеулер XOZ жазықтығындағы екі түзуді анықтайды.

XOZ жазықтықтығына параллель жазықтықтағы қимасы гипербола болады. Шынында да егер гиперболалалық параболидты z=h жазықтығымен қисақ, қимасында 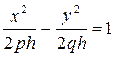деген гипербола шығады. Осы қималардың көмегімен гиперболалық параболоидтың түрі анықталады.