Нүкте кинематикасы. Нүкте қозғалысын векторлық әдіспен анықтау

Векторлық әдіс.Қозғалушы М нүктесінің кез келген t уақыт кезеңіндегі орны r радиус векторымен, ал келесі t₁=t +∆t уақыт кезеңіндегі М₁ орны r₁=r +∆r радиус векторымен анықталса, сонда М нүктесінің элементар ∆t уақыт ішіндегі орын ауыстыруы мынадай болады:

ММ₁=r₁ – r= ∆r

Осы вектордың өзіне сәйкес ∆t уақыт өсісшесіне қатынасы:

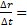v_oрт

М нүктесінің сол уақыт ішіндегі орташа жылдамдығы деп аталады. Нүктенің орташа жылдамдығы оның радиус векторының өсімшесімен бағыттас.

Орташа жылдамдықтың ∆t нөлге ұмтылғандағы шегі v нүктенің t уақыт кезеңіндегі сызықтық жылдамдығы деп аталады,

v= = ;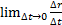

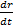Орташа үдеудің ∆t нөлге ұмтылғандағы шегі М нүктесінің үдеуі деп аталып, а арқылы белгіленеді:

а= = ;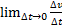

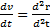16. Нүкте кинематикасы. Нүкте қозғалысын координаттық әдіспен анықтау. Уақыт өткенде бір нүктеден екінші нүктеге орын ауыстырғанда, дене (материалдық нүкте) дене қозғалысының траекториясы деп аталатын қандай да бір қисықты сызады. Материалық нүктенің кеңістіктегі орны белгілеп алынған декарттық координаталар жүйесіндегі x, y, z координаттары арқылы анықталады.
Нүктенің қозғалысы берілген деп есептеледі, егер нұкте координаталары үздіксіз және екі рет дифференциалданатын функциялар болып берілсе: x = f₁(t), y = f₂(t), z = f₃(t) (координаттардың уақыттан тәуелділігінен анықталады) теңдеулері -нүкте қозғалысының теңдеулері.
Дененің орын ауыстыруы деп дененің бастапқы орнын оның кейінгі орнымен қосатын бағытталған кесіндіні айтады. Орын ауыстыру – векторлық шама.
Жүрген жолы - дененің белгілі t уақыттың ішінде траектория доғасының ұзындығына тең болады. Жол – скалярлық шама.

17. Нүкте кинематикасы. Нүкте қозғалысын табиғи әдіспен анықтау.Нүктенің траекториясы беріліп, нүктенің берілген траектория бойымен қозғалысының заңы деп аталатын S=S(t) функциясы белгілі болса, нүктенің қозғалысы табиғи әдіспен берілген дейміз. Нүктенің бастапқы орны О нүктесінде болып, одан кейін нүкте траектория бойымен бір бағытқа ғана қозғалса, доғалық координата уақыттың монотонды функциясы болады.

Жылдамдық мынаған тең болады: v_τ= |S|.

Мұнда S>0 (v=S) болса, нүкте доғалық координатының оң бағытында, ал S<0 (v=-S) болса –қарсы бағытта қозғалыста болғаны. v_τ= S алгебралық жылдамдық деп аталады.

18. Динамиканың аксиомалары.Классикалық механиканың негізінде аксиомалар ретінде қабылданатын, Ньютонның заңдары жатады. Оларды Ньютон 1686 жылы «Натуралық философияның математикалық негіздері» деп аталатын шығармада алғашқы рет келтірген. Аксиомалар қазір математикалық дененің ең қарапайым моделі – материалық нүктеге қолданылып тұжырымдалады.

1.Инерциялық деп аталатын, оған қатысты ешбір күш әсер етпейтін немесе теңдестірілген күштер жүйесі әсер ететін материалық нүкте өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын сақтайтын санақ жүйелері бар.

2. Материалық нүктенің инерциялық санақ жүйесіне қатысты үдеуі нүктеге әсер етуші күшке пропорционал және күшпен бағыттас.

Матеиалық нүктеге түсірілген күшті F деп белгілеп, ал инерциялық санақ жүйесіне қатысты нүкте үдеуін а деп белгілесек, онда ma = F.

3.Екі материалық нүкте біріне бірі, бұл нүктелерді қосатын түзу бойымен қарама-қарсы бағытталған, модульдері тең күштермен әсер етеді, яғни F₁=-F₂.

Демек, үшінші аксиома екі материалық нүктелердің өзара шарттарын анықтайды.

4. Күштер жүйесі әсерінен нүктенің үдеуі әрбір күш жеке әсер еткендегі үдеулердің векторлық қосындысына тең, яғни (F₁, F_2, …, F_N) – нүктеге әсер ететін күштер жүйесі болса, онда а = ∑а_к, Мұнда а_к= ;

Сөйтіп, төртінші аксиома күштердің супперпозицялық немесе әсерлерінің тәуелсіздігі принйпін тұжырымдайды.

19. Материалық нүкте қозғалысының дифференциальдық теңдеулері.Декарт координаттық өстеріне (базисы i,j, k ) проекцияланған түрдегі нүкте қозғалысының дифференциалдық теңдеулері:

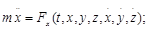
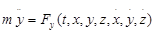
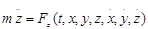
Мұнда 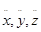- нүкте үдеуінің координаталық өстерге проекциялары F_x, F_y, F_z – нүктеге әсер етуші күштің осы өстерге түсірілген проекциялары.

20. Материалық нүкте динамикасының негізгі екі мәселесі.Материалық нүкте қозғалысының диффереренциалдық теңдеулерінің негізінде нүкте динамикасында негізгі екі мәселе шешіледі.

Нүкте динамкасының бірінші мәселесінде массасы m нүкте қозғалысының берілген заңы бойынша, осы заңдылықта болатын қозғалысты тудыратын күшті табу керек. Бұл мәселені жиі, берілген қозғалысты қамтамасыз ететін әсерлерді анықтауда талап ететін басқару есебі аумағында қарастырады.

Нүкте динамкасының екінші мәселесінде берілген күштер және қозғалыстың бастапқы шарттары бойынша нүкте қозғалысын анықтау керек, мұнда күштер, қозғалыс беруге пайдаланылған, айнымалылардың функциясы ретінде болуы керек. Бұл мәселені шешу үшін екінші ретті үш дифференциалдық теңдеулер жүйесін интегралдауға келтіріледі, шешімде анықтау керек болатын тұрақты шамалар пайда болады.

2. Материалдар кедергісі

1. Материалдар кедергісі. Негізгі түсініктер. Есептеуде қабылданған негізгі болжамдар.Материалдар кедергісі - машиналар мен конструкциялардың элементтерін беріктікке, қатаңдыққа және орнықтылыққа есептеудің негізін құрайтын ғылым.

Беріктік – құрылымның немесе оның жеке бөліктерінің сыртқы күш әсеріне қирамай, қарсыласу қабілетін айтамыз

Қатаңдық– құрылымның немесе оның жеке бөліктерінң сыртқы күш әсерінен болатын деформацияға қарсыласу қабілеті

Орнықтылық – құрылымның немес оның жеке бөліктерінң сыртқы күштің әсерінде серпімді тепе-теңдік бастапқы қалпын сақтау болып табылады.

Сыртқы кштер әсерінен денелер дефомацияланады, яғни өзінің өлшемдірімен калыптарын өзгертеді. Егер күш белгілі бір мәннен аспаса деформация күштің өсуіне пропорционал артады, ал күш әсерін тоқтатса, дене бастапқы қалпына келеді. Денеің бұл қасиетін серпімділік дейді. Шамасы айтарлықтай үлкен сыртқы күш әсерінен денеің қирамай, қайтымсых деформациялану қасиетін пластикалық (созылымдылық) деп атаймыз.

Беріктікке есептеуде екі әдіс қолданылады:

1) мүмкін кернеулер әдісі – брустардағы ең үлкен кернеу таңбасымен белгіленетін кернеуден аспауы талап етіледі.

2) қирату күштер әдісі – брус өлшемі берілетін жағдайда оның ұзақ мерзім жұмыс істеуі кезіндегі ешқандай өзгеріске ұшырамайтынын, яғни күш әсеріне төзімділігін анықтау есептері қарастырылады.

Серпімді орын ауыстыруларды шектеуге арналған есептер қатаңдыққа есептеу д.а.

Тепе-теңдік формасының тармақталуы басталатын сығу күшінің ең аз мәні кризистік күш д.а. сол күшті болдырмайтын, яғни бастапқы (түзу сызықты) қалпын сақтауға арналған есеп орнықтылыққа есептеу д.а.