Часть 2. Задания этой части выполняйте с записью решения. Кафедра естественно – математического образования
Кафедра естественно – математического образования
СБОРНИК
Экзаменационных работ для подготовки к итоговой аттестации по алгебре выпускников 9-х классов
Ханты – Мансийск
2008 г.
Автор – составитель Яковлева Людмила Сергеевна,доцент кафедры естественно – математического образования бюджетного учреждения дополнительного профессионального образования ХМАО – Югры «Институт развития образования», Почетный работник высшего профессионального образования Российской Федерации.
Рецензенты:
Котельникова Г.Н.,к.п.н., профессор, проректор по учебно – методической работе «Института развития образования ХМАО - Югры».
Чернущенко Н.Н.,учитель математики высшей категории МОУ СОШ № 3
г. Ханты – Мансийска.
Сборник экзаменационных работ для подготовки к итоговой аттестации по алгебре выпускников 9-х классов ХМАО – Югры: Методическое пособие для учащихся 9 – х классов ОУ, учителей математики и методистов /авт.– сост. Л.С. Яковлева. – Ханты – Мансийск, 2008г. – 66 с.
Методическое пособие предназначено для подготовки выпускников основной школы к итоговой аттестации по алгебре. В нем содержится 25 вариантов тренировочных экзаменационных работ, каждая из которых состоит из двух частей. Первая из них ориентирована на проверку знаний базового уровня программного материала по алгебре, а вторая часть – на повышенный уровень сложности.
Варианты составлены в полном соответствии с нормативными документами новой формы аттестации по алгебре за курс основной школы общеобразовательных учреждений. Ко всем заданиям даны ответы.
.Данное пособие будет полезным для учащихся и учителей математики при подготовке к выпускному экзамену за курс основной школы, а так же может быть использовано абитуриентами для подготовки к вступительным экзаменам в ССУЗы и к Единому государственному экзамену выпускниками полной школы.
Содержание.
1. Введение………………………………………………………………… 4 – 5 стр.
2. Советы выпускникам …………………………………………………. 5 стр.
3. Система оценивания экзаменационной работы……………………... 6 стр.
4. Варианты экзаменационных работ……………………………………7 – 51 стр.
5. Ответы…………………………………………………………………..51– 54 стр.
6. Дополнительные упражнения для подготовки к экзамену
различной степени трудности………………………………………...55 – 64 стр.
7. Литература……………………………………………………………… 65 стр.
Настоящее пособиепредназначено для самостоятельной, или под руководством учителя, подготовкек итоговой аттестации выпускников по алгебре за курс основной школы.
Пособие составлено в полном соответствии с нормативными документами и рекомендациями об апробации новой формы аттестации по алгебре выпускников 9 классов общеобразовательных учреждений.
Итоговая аттестационная работа состоит из двух частей.
Первая часть содержит 16 заданий в соответствии с программным материалом «Обязательного минимума содержания образования» по математике для основной школы. Эта часть направлена на проверку базовой подготовки выпускников по алгебре. Она включает в себе задания трех типов:
· задания, в которых требуется выбрать один верный ответ из четырех предложенных;
· задания с кратким ответом, в которых требуется записать только ответ;
· задания на сопоставление, в которых требуется соединить пары объектов (произвольным образом по смыслу задания).
Вторая часть содержит задания повышенной трудности трех уровней, оцениваемые 2, 4 и 6 баллами, если выпускники сдают экзамен по модели № 1, или 2, 3 и 4, если сдают по модели № 2. При выполнении этих заданий необходимо применить нестандартные приемы, уметь грамотно записывать решения с обоснованием рассуждений.
В пособии имеются дополнительные задачи высокого уровня сложности из различных разделов курса алгебры основной школы.
Критерии и порядок оценивания экзаменационной работы, перевод баллов в школьную отметку указаны в соответствии требованиям Министерства образования и науки Российской Федерации.
Варианты экзаменационных работ
Вариант 1.
Часть 1.
1.Найдите значение выражения 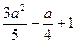 при а = -
при а = - 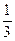 .
.
1). 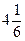 ; 2).
; 2). 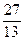 ; 3). -
; 3). - 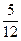 ; 4).
; 4). 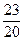 .
.
2. Запишите число 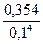 в стандартном виде.
в стандартном виде.
1). 35,4 · 10 2; 2). 3,54 · 10 2; 3). 3,54 · 10 3; 4). 3,54 · 10 - 3;
3. Известно, что число т четное. Какие из следующих чисел являются четными?
1). т – 3; 2). т + 4; 3). 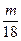 ; 4). т2 + 5.
; 4). т2 + 5.
4. В классе 12 учащихся получили за контрольную работу по математике отметку «хорошо», что составляет 40 % всех учащихся. Сколько всего учеников в классе?
1). 25; 2). 30; 3). 36; 4). 48.
5. Найдите площадь квадрата со стороной, равной (2 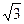 + 1) см.
+ 1) см.
Ответ:_____________
6. Упростите выражение 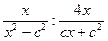 .
.
1). 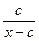 ; 2).
; 2). 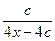 ; 3).
; 3). 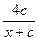 ; 4).
; 4). 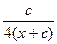
7. Решите систему уравнений 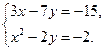
1). (2; 3); 2). (- 2; 3); 3). (2; - 3); 4). (- 2; - 3).
8. Какое из данных чисел принадлежит области определения выражения 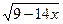 ?
?
1). 3; 2). – 15; 3). 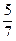 ; 4). 0,75.
; 4). 0,75.
9. Является ли число 29 членом арифметической прогрессии - 8; - 5; - 2; 1; … ?
Ответ: ____________
10. Сколько целых решений имеет неравенство 2х 2 – 3х +1 ≤ 0
1). 2; 2). 3; 3). ни одного; 4). 1.
11. Моторная лодка за одно и то же время может пройти 42 км по течению или 34 км против течения. Скорость течения реки 2,5 км/ч. Какова собственная скорость лодки?
1). 42(х – 2,5) = 34(х + 2,5); 2). 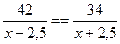 ; 3).
; 3). 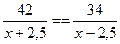 ;
;
4). 42(х – 2,5) = 34(х + 2,5);
12. Известно, что х > у. Сравните числа: (х – у) и (у - х ).
Ответ: ____________
13. Найдите сумму квадратов корней уравнения х 2(х – 4) – (х – 4) = 0.
1). 18; 2). 16; 3). 4; 4). 36
14. Используя графическое изображение, подберите первое уравнение системы так, чтобы система имела одно решение. 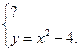 Если
Если 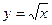 , то сколько решений имеет система?
, то сколько решений имеет система?
Ответ: _____________
15. Какое выражение является квадратом одночлена 0,3с 2(а 2т 5) 4?
1). 0,9 с 4а 14т 20 ; 2). 0,09 с 4а 16т 40; 3). 0,03 с 4а 8т 40 ; 4). 0,09 с 4а 14т40.
16. Дана функция f (x) = ах 2 + bх + с. На каком из рисунков изображен график этой функции, если известно, что коэффициент а > 0 и квадратный трехчлен
ах2 +bх +с имеет два положительных корня?
1). 2). 3). 4).
 |
Часть 2.Задания этой части выполняйте с записью решения.
1.(2 балла). Упростите выражение 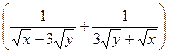 ·
· 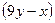 .
.
2. (4 балла). Решите уравнение: 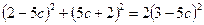 .
.
3. (4 балла). Найдите b, если известно, что числа (b – 3), 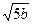 , (b + 16) являются
, (b + 16) являются
последовательными членами геометрической прогрессии.
4. (6 баллов). Решите неравенство 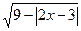 < 4.
< 4.
5. (6 баллов). Два трактора, работая вместе, могут вспахать поле за 12 часов. Если бы сначала половину поля вспахал первый трактор, а затем второй трактор вспахал оставшуюся часть, то на вспашку поля было бы затрачено 27 часов. За какое время может вспахать это поле каждый трактор, работая отдельно?
Вариант 2.
Часть 1.
1. Укажите наибольшее из чисел: 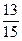 ; 0,78;
; 0,78; 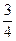 ;
; 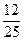 .
.
Ответ: ____________
2 Среди учеников класса 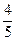 составляют мальчики. Сколько процентов составляет количество девочек от количества мальчиков?
составляют мальчики. Сколько процентов составляет количество девочек от количества мальчиков?
1) 50 %; 2) 25 %; 3) 20 %; 4) 200 %;
3. Найдите значение выражения 6 – 0,2 х 2 – 27 х 3 при х = - 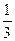 .
.
1) 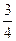 ; 2) 4
; 2) 4 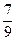 ; 3)
; 3) 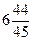 ; 4)
; 4) 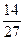 .
.
4. Из формулы у = 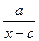 выразите переменную х.
выразите переменную х.
1) х = 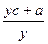 ;2) х = с -
;2) х = с - 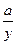 ;3) х = ус+ а ; 4) х =
;3) х = ус+ а ; 4) х = 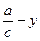 .
.
5. Какая из следующих дробей тождественно рана дроби 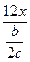 ?
?
1) 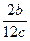 ; 2)
; 2) 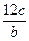 ; 3)
; 3) 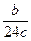 ; 4)
; 4) 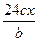 .
.
6. Укажите наименьший корень уравнения 6х2- х – 1 = 0.
Ответ _____________
7. Найдите значение выражения (1,5 · 10 -3 ) 2 .
1).2250000 2).0,0000000225 3). 0,00000225 4).2250000000
8. Одна из точек, отмеченных на координатной прямой, соответствует числу 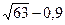 . Какая это точка?
. Какая это точка?
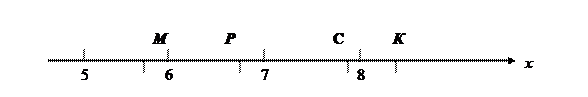
 1). М 2). Р 3). С 4). К
1). М 2). Р 3). С 4). К
9. Укажите наибольший корень уравнения 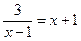 .
.
Ответ_________________
10. В классе количество девочек на 5 меньше количества мальчиков. Каждая девочка на празднование Нового года принесла 7 штук печенья, а каждый мальчик из общего количества принесенного печенья до празднования съел по 2 печенья, в результате чего к началу праздника осталось 40 штук. Пусть в классе х мальчиков и у девочек. Какая система уравнений соответствует условию задачи?
1) 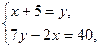 2).
2). 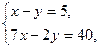 3)
3) 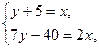 4).
4). 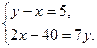
11. Упростите выражение 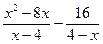 .
.
1). 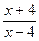 ; 2).
; 2). 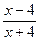 ; 3).
; 3). 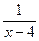 ; 4).
; 4). 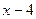 .
.
12. Решите неравенство (х2 + 7) (2х – 9) 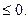
1). 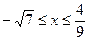 ,
, 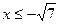 ; 2). -
; 2). - 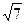
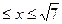 ; 3).
; 3). 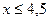 ; 4). х
; 4). х 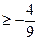 .
.
13. На первой странице книги 800 букв, а на каждой следующей на 10 меньше, чем на предыдущей. Сколько букв на странице с номером п?
1). 880 -10п; 2). 790 – 10п;3). 810 – 10п;4). 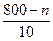 .
.
|
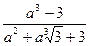 .
. Ответ: _______________ 
 15. График какой функции изображен на рисунке7
15. График какой функции изображен на рисунке7
1). у = 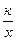 ; 2). у = -
; 2). у = - 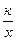 ; 3). у = х2;4). у = х + 2.
; 3). у = х2;4). у = х + 2.
16. Найдите среднее пропорциональное корней уравнения х2 – 13х+ 36 = 0.
1). 4; 2). 6; 3). 8; 4). 0,5.
Часть 2.Задания этой части выполняйте с записью решения
1. (2 балла ) Упростите выражение 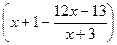 :
: 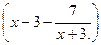
2. (4балла) Решите уравнение 10х 4 – 45х = 30х 2 – 15 х 3.
3. (4 балла) Постройте график функции у = х + 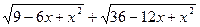 .
.
4. (6 баллов) В куске сплава меди и цинка количество меди увеличили на 40 %, а количество цинка уменьшили на 40 %. В результате общая масса куска сплава увеличилась на 20%. Определить процентное содержание меди и цинка в первоначальном куске сплава.
5. (6 баллов) Найдите все значения а, при которых точка пересечения прямых
3х + ау + 1 = 0 и 2х - 3у - 4 = 0 находятся в третьей координатной четверти.
Вариант 3.
Часть 1.
1. Найдите десятичную дробь, равную 64,85 10 - 7.
1). 0,06485 ; 2). 0,0006485 ; 3). 0,000006485; 4). 0,00006485.
2. Цена товара сначала повысилась на 14 %, а затем новая цена снизилась на 9 % от новой цены. Сравните последнюю цену товара с первоначальной ценой.
1). цена стала выше; 2). не изменилась; 3). цена стала ниже; 4). для ответа не хватает данных.
3. Найдите значение выражения: 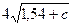 , если с = - 1,45.
, если с = - 1,45.
1). 12; 2). 1,2 ; 3). 0,12; 4). 3,6.
4. Из формулы площади правильного шестиугольника 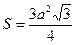 сторону а.
сторону а.
1). 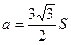 ; 2).
; 2). 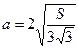 ; 3).
; 3). 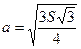 ; 4).
; 4). 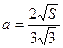 .
.
5. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
1). 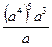 ; 2).
; 2). 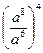 ; 3).
; 3). 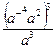 ; 4)..
; 4).. 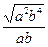
а). а- 9; б) а 22; в). а 8; г). b.
6. Запишите многочлен 3 п (1 – п) + (п + 2) (4 – п) в стандартном виде:.
Ответ: __________________
7. Найдите произведение корней уравнения: 2 х 2 – 19 х + 9 = 0.
1). 5 ; 2). 4,2 ; 3). 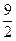 ; 4). 2,25.
; 4). 2,25.
8. Упростите выражение: 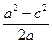 ·
· 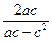 .
.
Ответ: ____________
9. Последовательность задана формулой сп = 2п3 - 1. Какое из чисел является членом этой последовательности?
1). - 32 ; 2). 21 ; 3). - 17 ; 4). 56
10. На рисунке изображен график функции у = 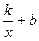 . Определите знаки коэффициентов k и b.
. Определите знаки коэффициентов k и b.
|
|
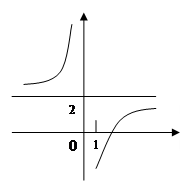
11. Аквариум с прямоугольным дном занимает на столе площадь, равную 465 см2. Ширина дна аквариума на 16 см меньше длины. Найдите ширину дна аквариума.
1). 31; 2). 15; 3). 46; 4). 18.
12. Решите систему неравенств: 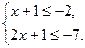
Ответ: ______________
13. График линейной функции - прямая, проходящая через точку А (3; 2). Ее угловой коэффициент равен – 4. Определите формулу, которой задается эта функция.
1). 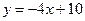 ; 2).
; 2). 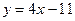 ; 3).
; 3). 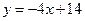 ; 4).
; 4). 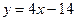 .
.
14. Решите неравенство: | 4 х - 7 | > 9.
1). х < - 0,5; х < 4; 2). х < - 0,5; х > 4; 3). х - 0,5 < х < 4;4). х > - 0,5; х > 4.
15. Найдите значение выражения: 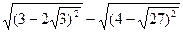
1). 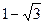 ; 2).
; 2). 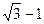 ; 3). – 7 -
; 3). – 7 - 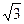 ; 4).
; 4). 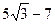 .
.
16. Сократите дробь: 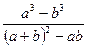 .
.
Ответ: ___________
Часть 2.Задания этой части выполняйте с записью решения.
1. ( 2 балла). Упростите выражение 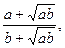 (а < 0, b < 0).
(а < 0, b < 0).
2. ( 4 балла). Лодка плывет от А до В по реке 4 суток, а от В до А – 5 суток. Во сколько раз скорость движения лодки по течению больше скорости течения реки?
3. ( 4 балла). Чему равен остаток от деления квадрата нечетного числа на 8?
4. ( 6 баллов). Решите систему уравнений: 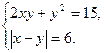
5. ( 6 баллов). Найдите все значения параметра р, для которого квадратное уравнение х2 – 2рх + р + 6 = 0 имеет положительные корни.
Вариант 4.
Часть 1.
1. Велосипедист двигался со скоростью 16,2 км/ч. Выразите эту скорость в м/сек.
1). 5,6 м/сек; 2). 1,62 м/сек; 3). 4,5 м/сек; 4). 2 м/сек.
2. Утром в магазин привезли в 4 раза больше батонов, чем булочек. К вечеру было продано 88% батонов и половину булочек. Чего осталось продать больше: булочек или батонов?
1). булочек; 2). батонов; 3). поровну; 4). для ответа не хватает данных.
3. Найдите значение выражения 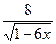 при х = 0,06.
при х = 0,06.
1). – 10; 2). 10; 3). 0,01; 4). 0,1.
4. Из формулы объема шара 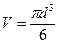 найдите диаметр d.
найдите диаметр d.
1). 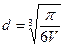 ; 2).
; 2). 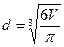 ; 3).
; 3). 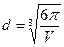 ; 4).
; 4). 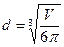 .
.
5. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки.
1). 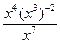 ; 2).
; 2). 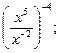 3).
3). 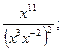 4).
4). 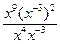 .
.
а). х2 ; б). х-9 ; в). х9 ; г). х-28 .
6. Решите уравнение 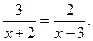
7. Какие из выражений: 1). 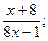 2).
2). 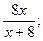 3).
3). 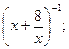 4).
4). 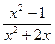 не имеют смысл при х = 0 ?
не имеют смысл при х = 0 ?
Ответ: ____________
8. Упростите выражение: 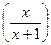 ·
· 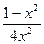 .
.
Ответ: ___________
9. В угловом секторе стадиона в первом ряду имеется 7 мест, а в каждом следующем ряду на 2 места больше, чем в предыдущем. Сколько мест в 26 ряду?
1). 54; 2). 57; 3). 63; 4). 49.
10. На рисунке изображен график функции 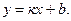 Определите знаки коэффициентов k и b.
Определите знаки коэффициентов k и b.
1). k < 0 и b < 0; 2). k < 0 и b > 0; 3). k > 0 и b > 0; 4). k > 0 и b < 0.
|
|

11. Решите неравенство: 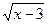 < 4.
< 4.
1). – 3 < х < 16; 2). 3 < х < 19; 3). х < 7; 4). 0 < х < 7.
12. Даны три числа: 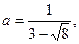
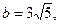
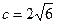 . Сравните их между собой.
. Сравните их между собой.
1). а < b < с ; 2). с < а < b; 3). а < с < b ; 4). с < b < а.
13. Найдите сумму хо + уо, если хои уо являются решениями системы 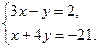
1). – 4; 2). 6; 3). – 6; 4). 4.
14. Упростите выражение: 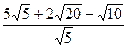 .
.
1). 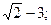 2).
2). 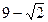 ; 3).
; 3). 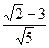 ; 4).
; 4). 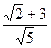 .
.
15. Представьте трехчлен в виде произведения: 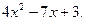
Ответ: _____________
16. Сумма цифр трехзначного числа равна 15. Если поменять местами цифру десятков и цифру единиц, то исходное число уменьшится на 9. Найдите это число, если цифра сотен меньше цифры десятков. на 5.
1). 206; 2). 726; 3). 276; 4). 672.
Часть 2.Задания этой части выполняйте с записью решения.
1. (2 балла). Решите уравнение 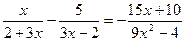 .
.
2. (4 балла). Запишите уравнение прямой, проходящей через точку А (- 15; - 16) и пересекающую ось х в точке с абсциссой, равной 9.
3. (4 балла). Сумма первых пяти членов арифметической прогрессии равна 27,5, а сумма следующих пяти ее членов равна 90. Найдите сумму членов этой прогрессии с одиннадцатого по пятнадцатый включительно.
4. (6 баллов). Решите систему неравенств 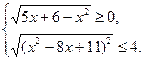
5. (6 баллов). Апельсины подешевели на 30 %. Сколько апельсинов можно теперь купить на те же деньги, на которые раньше покупали 2,8 кг?
Вариант 5.
Часть 1.
1. Найдите значение выражения: (15,4 · 10 – 3) : (5 · 10 – 5).
1). 3,08; 2). 0,0308; 3). 30,8; 4). 308.
2. Вкладчик должен положить деньги в один из банков. Первый банк обязуется через год вернуть 110% годовых, а второй - 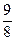 от вложенной суммы. В какой банк выгодно вкладчику положить деньги?
от вложенной суммы. В какой банк выгодно вкладчику положить деньги?
1). во второй; 2). в первый; 3). в любой; 4). для ответа не хватает данных.
3. Из формулы площади равнобедренного треугольника 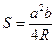 найдите боковую сторону а.
найдите боковую сторону а.
1). 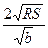 ; 2).
; 2). 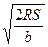 ; 3).
; 3). 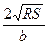 ; 4).
; 4). 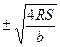 .
.
4. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
1). 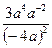 ; 2).
; 2). 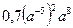 ; 3)..
; 3).. 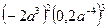 ; 4).
; 4). 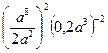 .
.
а). 0,7а – 2; б). 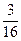 ; в). 6,25а 6; г). 0,032а – 6.
; в). 6,25а 6; г). 0,032а – 6.
5. Найдите значение выражения 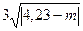 , если т = 5,04.
, если т = 5,04.
1). – 2,7; 2). 2,7; 3). 3,4; 4). 6,3.
6. Лодка проплыла 10 км по течению реки и 9 км против течения, затратив на путь против течения на 1 час больше, чем на путь по течению. Найдите собственную скорость лодки, если скорость течения 2 км/ч.
Пусть х км/ч – собственная скорость лодки. Какое из следующих уравнений соответствует условие задачи?
1). 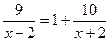 ; 2).
; 2). 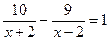 ; 3).
; 3). 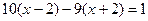 ;
;
4). 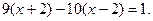
7. Найдите сумму убывающей геометрической прогрессии, если ее первый член равен 25, а знаменатель равен (- 0,25).
1). 18; 2). 20; 3) – 20; 4). – 18.
8. Используя график функции 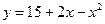 , решите неравенство
, решите неравенство 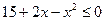 .
.
Ответ: ____________
9. Укажите наименьшее из чисел: 1,105; 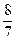 ;
; 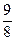 ;
; 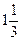 .
.
Ответ: ____________
10. Найдите сумму целых решений системы неравенств 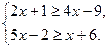
1). 7; 2). 9; 3). 14; 4). 12.
11. Упростите выражение: 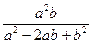 ·
· 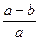 .
.
1). 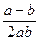 ; 2).
; 2). 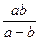 ; 3).
; 3). 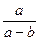 ; 4).
; 4). 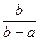 .
.
12. Расположите в порядке возрастания числа: 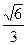 ;
; 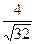 ;
; 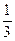 .
.
1). 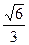 ;
; 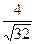 ;
; 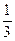 ; 2).
; 2). 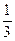 ;
; 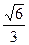 ;
; 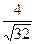 ; 3).
; 3). 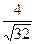 ;
; 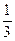 ;
; 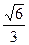 ; 4).
; 4). 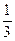 ;
; 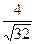 ;
; 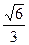 .
.
13.Найдите область определения функции f (x) = 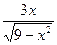 .
.
Ответ: __________
14. Решите систему уравнений: 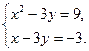
1). (- 3; 0), (4; 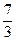 ); 2). (- 3;0), (
); 2). (- 3;0), ( 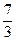 ; 4); 3). (0; - 3), (4;
; 4); 3). (0; - 3), (4; 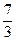 ); 4). (- 3;0), (4;
); 4). (- 3;0), (4; 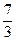 ).
).
15. Решите уравнение: | х + 1| = 3.
1). 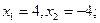 2).
2). 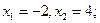
3). 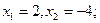 4).
4). 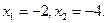
16. Укажите координаты точек пересечения линий: 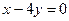 и
и 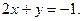
Ответ: ____________
Часть 2.Задания этой части выполняйте с записью решения.
1. (2 балла). Решите систему уравнений: 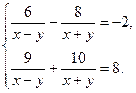
2. (4 балла). Найдите область значений функции 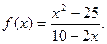
3. (4 балла). Сумма трех чисел, образующих арифметическую прогрессию, равна 30. Если от второго члена отнять 4, а от третьего отнять 5, то получится геометрическая прогрессия. Найдите эти числа.
4. (6 баллов). Найти все значения параметра р, при которых график функции 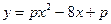 расположен ниже оси абсцисс.
расположен ниже оси абсцисс.
5. (6 баллов). Два сотрудника типографии вместе набрали на компьютере 65 страниц, причем первый работал на 1 час больше второго. Однако второй набирал в час на 2 страницы больше первого и поэтому он набрал на 5 страниц больше. Сколько страниц в час набирал каждый сотрудник?
Вариант 6.
Часть 1.
1. Найдите значения функции f(x) = 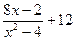 , если значение аргумента равно числу (- 5).
, если значение аргумента равно числу (- 5).
1). – 3; 2). 10; 3). 4; 4). 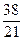 .
.
2. После снижения цены товара на 360 руб., его стоимость стала 2520 руб. На сколько процентов была снижена цена товара?
1). 14 %; 2). 12,5 %; 3). 10 %; 4). 125 %.
3. Упростите выражение: 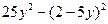 .
.
1). 4 – 10у; 2). 10у – 4; 3). – 4 + 20у; 4). 50у 2 – 4.
4. Известно, что т, п, р – отрицательные числа. Какое из указанных утверждений верно?
1). тп + р > 0; 2). тп + р < 0; 3). тп + р = 0; 4). знак суммы тп + р может быть любым.
5. Известно, что для сторон прямоугольного треугольника верно соотношение 
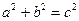 . Выразите из этой формулы сторону b.
. Выразите из этой формулы сторону b.
1). 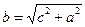 ; 2).
; 2). 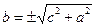 ; 3).
; 3). 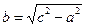 ; 4).
; 4). 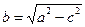 .
.
6. Укажите наибольшее целое число, принадлежащее области определения функции 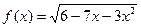 .
.
1) - 3; 2). 0; 3). 1; 4). 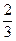 .
.
7. Расстояние между пунктами А и В равно 250 км. Автомобиль отправился из пункта А в В со скоростью 50 км/ч. Одновременно навстречу ему из В в А выехал мотоциклист со скоростью 40 км/ч. Расстояние между ними у является функцией от времени х, в течение которого они находились в пути. Задайте эту функцию формулой.
1) у = 250 – 90х; 2) у = 250 – 95х; 3) у = 250 - 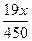 ; 4) у = 95х - 250.
; 4) у = 95х - 250.
8. Если дано неравенство - 6х < 4у – 2, то какие из указанных неравенств являются верными?
1). х < 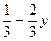 ; 2). х >
; 2). х > 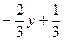 ; 3). у <
; 3). у < 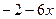 ; 4). у <
; 4). у < 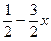 .
.
9. Решите систему уравнений: 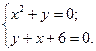
1). (- 2; - 4), (- 9; 3); 2). (3; - 9), (- 2; - 4); 3). (2; - 4), (3; - 9); 4). (- 9; 3), (4; - 2).
10. Сократите дробь: 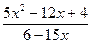 .
.
1). 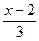 ; 2).
; 2). 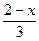 ; 3).
; 3). 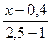 ; 4).
; 4). 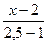 .
.
11. Упростите выражение: 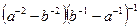 .
.
Ответ: ___________
12. Укажите наименьший корень уравнения: 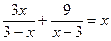 .
.
1). - 3; 2). – 2; 3). 1; 4). 3.
13. Выписано несколько членов арифметической прогрессии: - 7; - 4; - 1; 2; 5; … Найдите сумму первых десяти членов этой прогрессии.
1). 69; 2). 65; 3). 73; 4) 18.
14. Разложите многочлен на множители: 1 – х2 + 2ху – у2.
Ответ: _____________
15. Найдите множество значений функции у = - х2 – 4х + 5.
1). 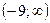 ; 2).
; 2). 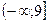 ; 3).
; 3). 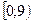 ; 4).
; 4). 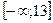 .
.
16. Найдите значение выражения: 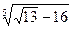 ·
· 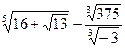 +
+ 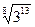 ·
· 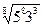 .
.
1). 37; 2). 52; 3). 47; 4). - 10.
Часть 2.Задания этой части выполняйте с записью решения.
1. (2 балла). Из города А в город В, расстояние между которыми 300 км, выехал автобус. Через 20 мин навстречу ему из В в А выехал автомобиль и через 2 часа после выезда встретил автобус. С какой скоростью ехал автомобиль, если известно, что она была на 20 км/ч больше скорости автобуса?
2. (4 балла). Сократите дробь: 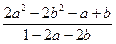 .
.
3. (4 балла). Решите систему уравнений: 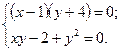
4. (6 баллов). При каких значениях р корни уравнения 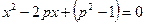 принадлежат промежутку
принадлежат промежутку 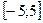 ?
?
5. (6 баллов). Найдите наибольшее целое решение неравенства
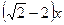 >
> 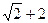 .
.
Вариант 7.
Часть 1.
1. Упростите выражение 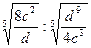 .
.
1) 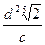 ; 2)
; 2) 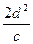 ; 3)
; 3) 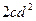 ; 4)
; 4) 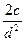 .
.
2. Василий может решить адачу за 35 мин., а Петр – за 30% отведенного на выполнение уроков времени. Кто из учащихся решит задачу быстрее, если на выполнение уроков отведено 2 часа 40 мин.?
1). Петр; 2). одновременно; 3). Василий; 4). для ответа не хватает данных.
3. Сравните | х | и х2, если - 2 < х < 2 .
1). | х | > х2 2). | х | = х2 3). | х | < х2; 4). нет таких значений.
4. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
1). 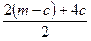 ; 2).
; 2). 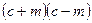 ; 3).
; 3). 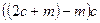 ; 4).
; 4). 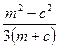 .
.
а). т + с; б). 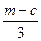 ; в). с2 - т2; г). 2с2.
; в). с2 - т2; г). 2с2.
5. Между какими целыми числами находится число 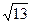 ?
?
1). 4 и 6; 2). 3 и 4; 3). 2 и 4; 4). 3 и 11.
6. Найдите значение выражения 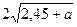 , если а = - 0,76.
, если а = - 0,76.
Ответ: __________
7. Площадь ромба с диагоналями d1и d2 вычисляется по формуле 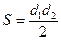 . Выразите из этой формулы d12.
. Выразите из этой формулы d12.
1). d12 = 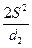 ; 2). d12 =
; 2). d12 = 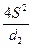 ; 3). d12 =
; 3). d12 = 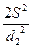 ; 4). d12 =
; 4). d12 = 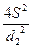 .
.
8. Миша спускается с горы на 20 мин быстрее, чем поднимается в гору. Путь в одном направлении составляет 1,5 км. Найдите скорость движения Миши при спуске с горы, если его скорость при подъеме на 2 км/ч меньше.
Пусть х км/ч – скорость движения Миши при спуске с горы. Какое уравнение соответствует условию задачи?
1). 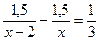 ; 2).
; 2). 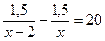 ; 3).
; 3). 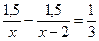 ;
;
4). 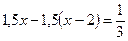 .
.
9. Выписаны несколько последовательных членов геометрической прогрессии: …, 81; 54; у; 24; … . Найдите неизвестный член прогрессии у.
Ответ: ___________
10. Известно, что х и у - положительные числа и х > у. Сравните выражения:
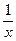 и
и 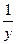 .
.
Ответ: ______________
11. На пост руководителя предприятия претендуют два кандидата. В голосовании приняли участие 287 депутатов, голоса которых распределились в отношении 2 : 5. Сколько голосов получил проигравший?
1). 205; 2). 82; 3). 41; 4). 164.
12. Вычислите координаты точек пересечения параболы 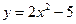 и прямой
и прямой
у = 4х – 5.
1). (0; 5) и (3; 2); 2). (0; - 5) и (2; 3); 3). (0; 2) и (- 5; 3); 4). (- 5; 0) и (2; 3).
13. Решите уравнение: 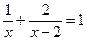 .
.
Ответ: ___________
14. Упростите выражение: 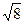 ·
· 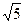 ·
· 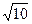 .
.
1). 40; 2). 20; 3). 25; 4). 16.
15. Решите систему неравенств: 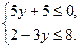
1). 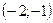 ; 2).
; 2). 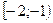 ; 3).
; 3). 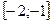 ; 4).
; 4). 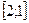 .
.
16. Упростите выражение: 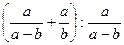 .
.
1). 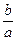 ; 2).
; 2). 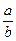 ; 3). ab; 4).
; 3). ab; 4). 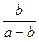 .
.
Часть 2.Задания этой части выполняйте с записью решения
1. (2 балла). Разложите многочлен на множители: 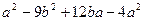 .
.
2. (4 балла). Выясните, имеет ли корни уравнение 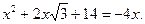
3. (4 балла). Найдите область определения выражения 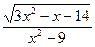 .
.
4. (6 баллов). Три числа образуют возрастающую арифметическую прогрессию, а их квадраты образуют геометрическую прогрессию. Найдите эти числа, если их сумма равна 42.
5.(6 баллов).При каких значениях параметра т вершины парабол 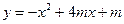 и
и 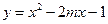 расположены по разные стороны от оси абсцисс?
расположены по разные стороны от оси абсцисс?
Вариант 8.
Часть 1.
1. Площадь клумбы равна 18,5 м2. Выразите эту площадь в км2.
1). 0,185 км2; 2). 0,00185 км2; 3).1,85 · 10 – 5 км2; 4).0,000000185 км2.
2. Банк выплачивает ежегодно 9,2 % от суммы вклада. Какой станет сумма вклада через год, если первоначальный вклад составляет 5800 рублей?
Ответ: ____________
3. При каких значениях т имеет смысл выражение 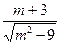 ?
?
1). т = 3; 2). т = 9; 3). т ≠ 3 и т ≠ - 3 ; 4). нет таких значений.
4. Площадь сферического сегмента радиуса R и высотой H вычисляется по формуле S = 2 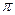 RH. Выразите из этой формулы высоту H.
RH. Выразите из этой формулы высоту H.
1). H = 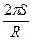 ; 2). H =
; 2). H = 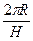 ; 3). H =
; 3). H = 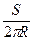 ; 4). H = 2
; 4). H = 2 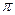 RS.
RS.
5. Какое выражение из верхней строки не встречается в нижней?
1). (х 2) 4 у 3 х 3; 2). (ху 4) 3 у 2; 3). 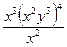 ; 4).
; 4). 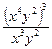 .
.
а). х 11у 3; б). х 9 у 4; в). х 11 у 6; г). х 9 у 12.
6. Вычислите сумму 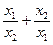 , если х1 и х2 являются корнями уравнения
, если х1 и х2 являются корнями уравнения
3х 2– 8х – 15 = 0.
1). 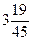 ; 2).
; 2). 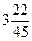 ; 3).
; 3). 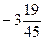 ; 4).
; 4). 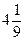 .
.
7. Упростите выражение: 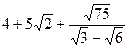 .
.
1). – 2; 2). – 1; 3). 4; 4). 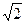 .
.
8. Чему равно наименьшее значение выражения 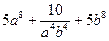 ?
?
1). 28; 2). 24; 3). 20; 4) 6.
9. Упростите выражение: 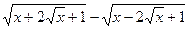 .
.
1). 3; 2). 1; 3). 2; 4) 0.
10. Решите неравенство: 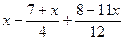 >
> 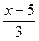 .
.
Ответ: ___________
11. В арифметической прогрессии члены а20 = 0, а21 = - 41. Найдите первый член прогрессии.
1). 760; 2). 779; 3). 802; 4). 690.
12. Отличная от нуля абсцисса точки пересечения графиков функций у = 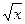 и
и
у = х (х – 1) принадлежит промежутку :
1). (0; 1); 2). (2; 3); 3). (3; 4); 4). (1; 2).
13. Гипотенуза прямоугольного треугольника больше одного из его катетов на 9 см и больше другого катета на 32 см. Найдите периметр треугольника.
1). 124 см ; 2). 154 см ; 3). 15,4 см ; 4). 163 см.
14. Укажите число, принадлежащее промежутку (3; 4).
1). 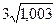 ; 2)
; 2) 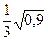 ; 3). 2; 4). 10.
; 3). 2; 4). 10.
15. Какое из чисел не является корнем уравнения: 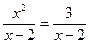 ?
?
1). 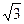 ; 2). 2; 3). -
; 2). 2; 3). - 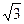 ; 4). 4.
; 4). 4.
16. Решите систему уравнений: 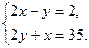
Ответ: _________________
Часть 2.Задания этой части выполняйте с записью решения
1. (2 балла). Упростите выражение : 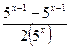 .
.
2. (4 балла). Найдите наименьшее целое значение параметра р, при котором уравнение х 2 + 2х + р = 0 не имеет корней.
3. (4 балла). Решите уравнение: 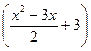 ·
· 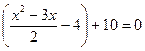 .
.
4, (6 баллов). Решите систему уравнений: 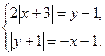
5. (6 баллов). Один пешеход проходит в минуту на 5 м меньше другого, поэтому на прохождение одного километра ему требуется на 50 секунд больше. Какое расстояние проходит каждый пешеход за один час?
Вариант 9.
Часть 1.
1. Упростите выражение: (т + 3)2 – (т – 2) (т + 2).
1). 2т2 – 3; 2). 6т + 13; 3). 2 – 5т; 4). 1 – т2.
2. Книга стоит 68 р. Выразите эту сумму в тысячах рублей.
1).6,8; 2). 0,0068; 3). 0,068; 4).0,00068.
3. Смешали 120 г муки, 80 г сахарного песка и 200 г сухих сливок. Какой процент смеси составляют сливки?
1). 8 %; 2). 50 %; 3). 35 %; 4).75 %.
4. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
1). 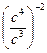 ; 2).
; 2). 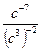 ; 3).
; 3). 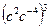 ; 4).
; 4). 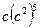 .
.
а). с 11; б). с -6; в). с -2; г). 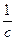 .
.
5. Из формулы площади объема пирамиды V = 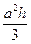 c квадратом в основании выразите длину основания а.
c квадратом в основании выразите длину основания а.
1). 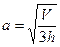 ; 2).
; 2). 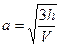 ; 3).
; 3). 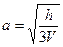 ; 4).
; 4). 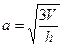 .
.
6. Разность между шестым и первым членами геометрической прогрессии равна 1210, а знаменатель прогрессии равен 3. Найдите сумму первых пяти членов этой прогрессии.
1). 515; 2). 725; 3). 605; 4). 1020.
7. Какое из чисел: 2016; 3924; 1782; 8244; 52308 не делится нацело на 36?
Ответ: _____________
8. Решите систему неравенств: 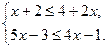
1). ( - 2; 2); 2). [ - 2; 2]; 3). 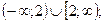 4). (- 2; 2].
4). (- 2; 2].
9. Вычислите: ( 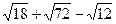 ) (
) ( 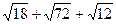 ).
).
1).140; 2). 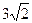 ; 3). 150; 4).
; 3). 150; 4). 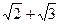 .
.
10. Зная, что х1 и х2 - корни уравнения 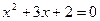 , найдите сумму
, найдите сумму
(х13 + х2 3 ).
1). – 18; 2). 9; 3). – 36; 4). 25.
11. Решите систему уравнений: 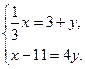
Ответ: ____________
12. Упростите выражение: 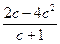 :
: 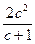 .
.
Ответ: ____________
13. На выполнение некоторой работы первый рабочий тратит на 3 часа меньше времени, чем второй. Работая вместе, они выполняют эту работу за 8 часов. Сколько времени требуется каждому рабочему на выполнение всей работы?
Составьте уравнение по условию задачи, приняв за х время, необходимое первому рабочему для выполнения всей работы.
1). 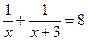 ; 2).
; 2). 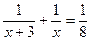 ; 3).
; 3). 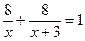 ; 4).
; 4). 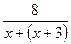 = 1.
= 1.
14. Разложите многочлен на множители: х 2у - х 3 – ху + х2 .
Ответ: _____________
15. Графику какой из указанных функций: у = 2х – 4, у = х 2 + 3х – 1, 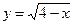 принадлежит точка М (20; 4)?
принадлежит точка М (20; 4)?
1). у = х 2 + 3х – 1; 2). у = 2х – 4; 3). 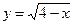 ; 4). ни одному графику.
; 4). ни одному графику.
16. Известно, что у < 0. Сравните у 3 и 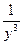 .
.
